3.1数系的扩充和复数的概念 课件 (共26张PPT)
文档属性
| 名称 | 3.1数系的扩充和复数的概念 课件 (共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 36.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第一课时
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
联系从自然数系到实数系的扩充过程,你能设想一种方法,使这个方程有解吗?
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
*
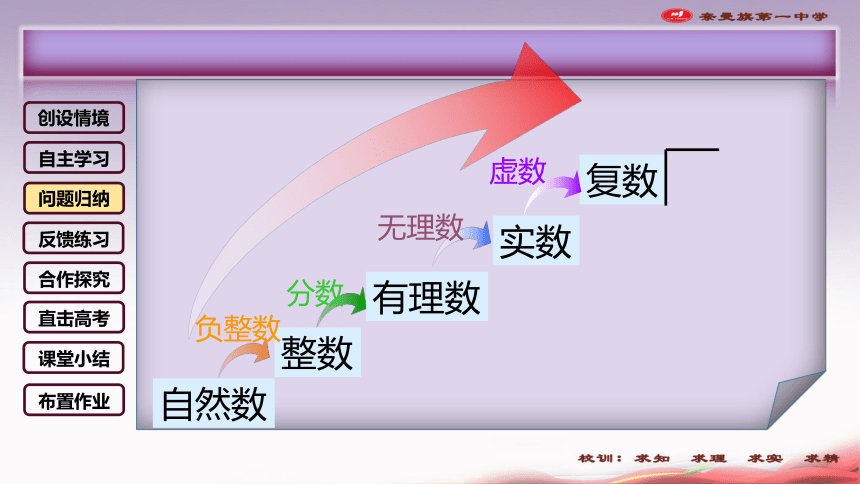
自然数
整数
有理数
实数
负整数
分数
无理数
回忆数的扩充
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
思考?
上述方程在实数中无解,联系从自然数系到实数系的扩充过程,能设想一种方法,使这个方程有解?
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
阅读教材50页至51页,思考一下问题:
1、虚数单位i是如何定义的?
2、什么是复数?
创设情境
反馈练习
合作探究
直击高考
课堂小结
为了解决负数开平方问题,数学家大胆引入一个新数 i ,把 i 叫做虚数单位,并且规定:
(2)实数可以与i 进行四则运算,在进行四则运算时,
原有的加法与乘法的运算律(包括交换律、结合律
和分配律)仍然成立.
注:虚数单位i是瑞士数学家欧拉最早引用的,它取自imaginary(想象的,假想的)一词的词头.
布置作业
自主学习
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
1、下列这些数与虚数单位i经过了哪些运算?
说一说
2、这些数的形式有什么共同点?你能用一个式子来表示这些数吗?
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
定义:把形如a+bi的数叫做复数(a,b 是实数)
其中i叫做虚数单位
复数全体组成的集合叫复数集,记作C
1、复数的概念
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
自然数
整数
有理数
实数
?
负整数
分数
无理数
复数
虚数
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
2、复数代数形式
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
观察下列复数,你有什么发现?
= -1
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
3、复数的分类
当b=0时,z是实数;
当b≠0时,z是虚数;
当a=0且b≠0时,z是纯虚数;
当a=0且b=0时,z是0
i不存在
i要存在
只有i
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
2、复数z=a+bi
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
1、即时训练
?若m+(m-1)i为实数,则m=( )
?若x+(2x-1)i为纯虚数,则x=( )
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
复数集与实数集、虚数集、纯虚数集之间有什么关系?
由上可知,实数集R时复数集C的真子集。
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
*
4、复数相等
注:两个虚数不能比较大小,只能由定义判断它们相等或不相等。
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
若2-3i=a-3i,求实数a的值;
2.若8+5i=8+bi,求实数b的值;
3.若4+bi=a-2i,求实数a,b的值。
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
解:根据复数相等的定义,得方程组
例3、已知 ,
其中 求 与 .
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
你能否找到用来表示复数的几何模型呢?
x
o
1
实数可以用数轴上的点来表示。
一一对应
规定了正方向,
直线
数轴
原点,
单位长度
实数
数轴上的点
(形)
(数)
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
一个复数由什么唯一确定?
Z=a+bi(a, b∈R)
实部!
虚部!
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(数)
(形)
一一对应
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
建立了平面直角坐标系来表示复数的平面---复平面
其中:x轴------实轴
y轴------虚轴
x
y
o
b
a
Z(a,b)
z=a+bi
复数z=a+bi
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
实数绝对值的几何意义
能否把实数绝对值概念
推广到复数范围呢?
实数a在数轴上所对应的点A到原点O的距离。
复数绝对值的几何意义
复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
例3 求下列复数的模:
(1)z1=-5i (2)z2=-3+4i (3)z3=5-5i
(4)z4=1+mi(m∈R) (5)z5=4a-3ai(a<0)
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
z = a + bi
(a,b∈R)
复数的分类
当b=0时z为实数;
当b?0时z为虚数;
当b?0且a =0时z为纯虚数.
复数的相等
a+bi=c+di
(a, b,c,d?R)
2、复平面
复数的模
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
作业布置:
教材54页
练习1、2、3
谢谢观看
第一课时
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
联系从自然数系到实数系的扩充过程,你能设想一种方法,使这个方程有解吗?
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
*
自然数
整数
有理数
实数
负整数
分数
无理数
回忆数的扩充
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
思考?
上述方程在实数中无解,联系从自然数系到实数系的扩充过程,能设想一种方法,使这个方程有解?
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
阅读教材50页至51页,思考一下问题:
1、虚数单位i是如何定义的?
2、什么是复数?
创设情境
反馈练习
合作探究
直击高考
课堂小结
为了解决负数开平方问题,数学家大胆引入一个新数 i ,把 i 叫做虚数单位,并且规定:
(2)实数可以与i 进行四则运算,在进行四则运算时,
原有的加法与乘法的运算律(包括交换律、结合律
和分配律)仍然成立.
注:虚数单位i是瑞士数学家欧拉最早引用的,它取自imaginary(想象的,假想的)一词的词头.
布置作业
自主学习
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
1、下列这些数与虚数单位i经过了哪些运算?
说一说
2、这些数的形式有什么共同点?你能用一个式子来表示这些数吗?
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
定义:把形如a+bi的数叫做复数(a,b 是实数)
其中i叫做虚数单位
复数全体组成的集合叫复数集,记作C
1、复数的概念
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
自然数
整数
有理数
实数
?
负整数
分数
无理数
复数
虚数
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
2、复数代数形式
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
观察下列复数,你有什么发现?
= -1
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
3、复数的分类
当b=0时,z是实数;
当b≠0时,z是虚数;
当a=0且b≠0时,z是纯虚数;
当a=0且b=0时,z是0
i不存在
i要存在
只有i
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
2、复数z=a+bi
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
1、即时训练
?若m+(m-1)i为实数,则m=( )
?若x+(2x-1)i为纯虚数,则x=( )
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
复数集与实数集、虚数集、纯虚数集之间有什么关系?
由上可知,实数集R时复数集C的真子集。
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
*
4、复数相等
注:两个虚数不能比较大小,只能由定义判断它们相等或不相等。
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
若2-3i=a-3i,求实数a的值;
2.若8+5i=8+bi,求实数b的值;
3.若4+bi=a-2i,求实数a,b的值。
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
解:根据复数相等的定义,得方程组
例3、已知 ,
其中 求 与 .
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
你能否找到用来表示复数的几何模型呢?
x
o
1
实数可以用数轴上的点来表示。
一一对应
规定了正方向,
直线
数轴
原点,
单位长度
实数
数轴上的点
(形)
(数)
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
一个复数由什么唯一确定?
Z=a+bi(a, b∈R)
实部!
虚部!
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(数)
(形)
一一对应
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
建立了平面直角坐标系来表示复数的平面---复平面
其中:x轴------实轴
y轴------虚轴
x
y
o
b
a
Z(a,b)
z=a+bi
复数z=a+bi
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
实数绝对值的几何意义
能否把实数绝对值概念
推广到复数范围呢?
实数a在数轴上所对应的点A到原点O的距离。
复数绝对值的几何意义
复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
例3 求下列复数的模:
(1)z1=-5i (2)z2=-3+4i (3)z3=5-5i
(4)z4=1+mi(m∈R) (5)z5=4a-3ai(a<0)
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
z = a + bi
(a,b∈R)
复数的分类
当b=0时z为实数;
当b?0时z为虚数;
当b?0且a =0时z为纯虚数.
复数的相等
a+bi=c+di
(a, b,c,d?R)
2、复平面
复数的模
创设情境
自主学习
问题归纳
反馈练习
合作探究
直击高考
课堂小结
布置作业
作业布置:
教材54页
练习1、2、3
谢谢观看
