2.1.2 向量的几何表示 课件 18张PPT
文档属性
| 名称 | 2.1.2 向量的几何表示 课件 18张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 500.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 11:31:34 | ||
图片预览






文档简介
(共18张PPT)
高中数学必修 4 第二章 平面向量
2.1.2向量的几何表示
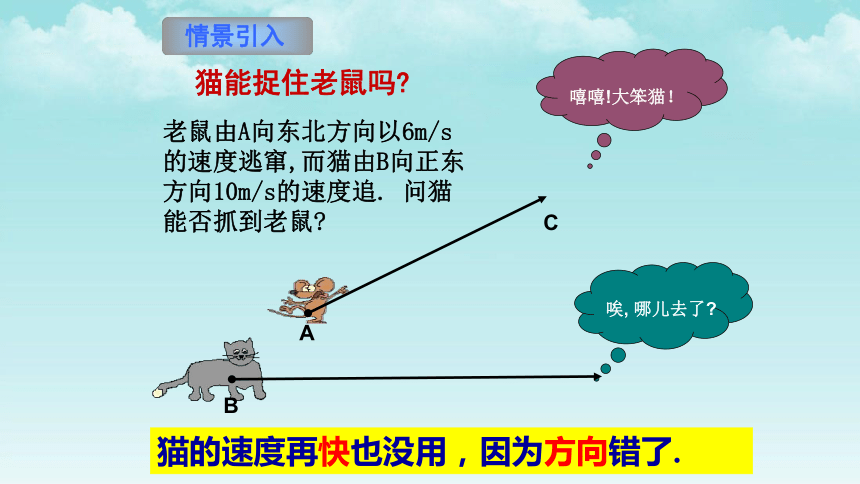
唉, 哪儿去了?
嘻嘻!大笨猫!
B
A
猫能捉住老鼠吗?
老鼠由A向东北方向以6m/s的速度逃窜,而猫由B向正东方向10m/s的速度追. 问猫能否抓到老鼠?
C
D
情景引入
猫的速度再快也没用,因为方向错了.
复习巩固
1、向量的概念
2、向量与数量的区别
既有大小,又有方向的量叫做向量.
只有大小,没有方向的量叫做数量.
定义上 :数量只有大小,向量有大小、有方向;
因为向量具有方向,所以向量之间不能比较大小。
引入课题
在上一节课中,我们学到了一个新的概念——向量,它是一个即有大小又有方向的量,那么在数学中,我们该如何表示呢?以及它的相关概念是如何定义的呢?本课将重点介绍向量的表示方法与相关概念.
引 言:
自主学习
请同学们阅读教材75页及76页,思考以下问题并完成导学案上的本节知识填空:
1.有向线段的概念及其三要素
2.向量的表示法
3.向量的模
4.特殊向量
5.平行向量
1.有向线段的概念及其三要素
(1)有向线段的概念
(2)有向线段的三要素
带有方向的线段
起点、方向、长度
(3)有向线段与向量的区别和联系
区别:从定义上看,向量有大小和方向两个要素,
而有向线段有起点、方向、长度三个要素.
因此,这是两个不同的量。
从位置上看,有向线段是固定的线段,
而向量是可以自由平移的.
联系:有向线段是向量的表示,并不是说向量就是有向线段.
问题探讨
2.向量的表示法
(1)几何表示:
(2)代数表示:
?印刷时,黑体小写字母a、b、c、 ;
书写时,带箭头的小写字母
A(起点)
B(终点)
a
有向线段表示
?有向线段的起点和终点字母,如,
问题探讨
做一做1 已知向量 如图所示,下列说法不正确的是( )?
解析:由向量的表示知,A,B,C正确,D不正确.
D
问题探讨
3.向量的模
4.特殊向量
向量 的大小——长度称为向量的模,记作 .
长度为0的向量叫做零向量,记作0. 方向任意
长度为1个单位长度的向量叫做单位向量.
说明:零向量、单位向量的定义都只是限制了大小.
问题探讨
5.平行向量
从方向的角度看:
方向相同或相反的非零向量,叫做平行向量,记作
规定:零向量和任意向量平行.
问题探讨
做一做2 判断下列说法是否正确,正确的在后面的括号内
打“√”,错误的打“×”.
(1)零向量只有大小没有方向.( )
(2)若向量 与向量 同向,且 则 ( )
(3) ( )
×
×
问题探讨
×
【例1】 下列说法正确的是( )
A.数轴是向量
B.方向不同的向量不能比较大小,但同向的向量可以比较大小
C.单位向量的模都相等
D.零向量是没有方向的
探究一 向量的概念及零向量、单位向量?
解析:数轴没有大小,故不是向量,A不正确;不管向量的方向如何,它们都不能比较大小,故B不正确;单位向量的模都是1,故C正确;零向量的方向是任意的,故D不正确.
C
问题探讨
变式训练1 下列说法中正确的是( )?
A.数量可以比较大小,向量也可以比较大小
B.向量的模可以比较大小
C.模为1的向量都是平行向量
D.由于零向量的方向不确定,故零向量不能与任意向量平行
解析:向量不能比较大小,故A不正确;向量的模是一个数量,可以比较大小,故B正确;平行向量的方向相同或相反,与模无关,故C不正确;规定零向量与任意向量平行,故D不正确.
B
问题探讨
【例2】给出下列说法:
①②④
探究二 平行向量?
问题探讨
变式训练2 如图,O是正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,在图中所示的向量中写出与 平行的向量.
分析:若向量平行,则向量所在直线平行或重合.
解:
问题探讨
平行
课堂小结
向量
向量的表示
零向量
向量关系
字母表示
几何表示
平行向量
向量的模
特殊向量
单位向量
这节课你学到了什么?
布置作业
2.(必做作业)教材77页 习题2.1A组:1、2、5.
3.(选做作业)向量既有大小,又有方向,如果两个向量大小和方向都相等,那么这两个向量有什么关系吗?请课后进行研究.
1.(必做作业)自主复习重要知识点.
谢谢欣赏!
生命因为勤勉的努力而精彩
青春因为执着的追求而绚丽
高中数学必修 4 第二章 平面向量
2.1.2向量的几何表示
唉, 哪儿去了?
嘻嘻!大笨猫!
B
A
猫能捉住老鼠吗?
老鼠由A向东北方向以6m/s的速度逃窜,而猫由B向正东方向10m/s的速度追. 问猫能否抓到老鼠?
C
D
情景引入
猫的速度再快也没用,因为方向错了.
复习巩固
1、向量的概念
2、向量与数量的区别
既有大小,又有方向的量叫做向量.
只有大小,没有方向的量叫做数量.
定义上 :数量只有大小,向量有大小、有方向;
因为向量具有方向,所以向量之间不能比较大小。
引入课题
在上一节课中,我们学到了一个新的概念——向量,它是一个即有大小又有方向的量,那么在数学中,我们该如何表示呢?以及它的相关概念是如何定义的呢?本课将重点介绍向量的表示方法与相关概念.
引 言:
自主学习
请同学们阅读教材75页及76页,思考以下问题并完成导学案上的本节知识填空:
1.有向线段的概念及其三要素
2.向量的表示法
3.向量的模
4.特殊向量
5.平行向量
1.有向线段的概念及其三要素
(1)有向线段的概念
(2)有向线段的三要素
带有方向的线段
起点、方向、长度
(3)有向线段与向量的区别和联系
区别:从定义上看,向量有大小和方向两个要素,
而有向线段有起点、方向、长度三个要素.
因此,这是两个不同的量。
从位置上看,有向线段是固定的线段,
而向量是可以自由平移的.
联系:有向线段是向量的表示,并不是说向量就是有向线段.
问题探讨
2.向量的表示法
(1)几何表示:
(2)代数表示:
?印刷时,黑体小写字母a、b、c、 ;
书写时,带箭头的小写字母
A(起点)
B(终点)
a
有向线段表示
?有向线段的起点和终点字母,如,
问题探讨
做一做1 已知向量 如图所示,下列说法不正确的是( )?
解析:由向量的表示知,A,B,C正确,D不正确.
D
问题探讨
3.向量的模
4.特殊向量
向量 的大小——长度称为向量的模,记作 .
长度为0的向量叫做零向量,记作0. 方向任意
长度为1个单位长度的向量叫做单位向量.
说明:零向量、单位向量的定义都只是限制了大小.
问题探讨
5.平行向量
从方向的角度看:
方向相同或相反的非零向量,叫做平行向量,记作
规定:零向量和任意向量平行.
问题探讨
做一做2 判断下列说法是否正确,正确的在后面的括号内
打“√”,错误的打“×”.
(1)零向量只有大小没有方向.( )
(2)若向量 与向量 同向,且 则 ( )
(3) ( )
×
×
问题探讨
×
【例1】 下列说法正确的是( )
A.数轴是向量
B.方向不同的向量不能比较大小,但同向的向量可以比较大小
C.单位向量的模都相等
D.零向量是没有方向的
探究一 向量的概念及零向量、单位向量?
解析:数轴没有大小,故不是向量,A不正确;不管向量的方向如何,它们都不能比较大小,故B不正确;单位向量的模都是1,故C正确;零向量的方向是任意的,故D不正确.
C
问题探讨
变式训练1 下列说法中正确的是( )?
A.数量可以比较大小,向量也可以比较大小
B.向量的模可以比较大小
C.模为1的向量都是平行向量
D.由于零向量的方向不确定,故零向量不能与任意向量平行
解析:向量不能比较大小,故A不正确;向量的模是一个数量,可以比较大小,故B正确;平行向量的方向相同或相反,与模无关,故C不正确;规定零向量与任意向量平行,故D不正确.
B
问题探讨
【例2】给出下列说法:
①②④
探究二 平行向量?
问题探讨
变式训练2 如图,O是正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,在图中所示的向量中写出与 平行的向量.
分析:若向量平行,则向量所在直线平行或重合.
解:
问题探讨
平行
课堂小结
向量
向量的表示
零向量
向量关系
字母表示
几何表示
平行向量
向量的模
特殊向量
单位向量
这节课你学到了什么?
布置作业
2.(必做作业)教材77页 习题2.1A组:1、2、5.
3.(选做作业)向量既有大小,又有方向,如果两个向量大小和方向都相等,那么这两个向量有什么关系吗?请课后进行研究.
1.(必做作业)自主复习重要知识点.
谢谢欣赏!
生命因为勤勉的努力而精彩
青春因为执着的追求而绚丽
