2.1.2 向量的几何表示 课件 22张PPT
文档属性
| 名称 | 2.1.2 向量的几何表示 课件 22张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 336.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 11:26:14 | ||
图片预览






文档简介
(共22张PPT)
人教A版高中数学必修4
课题:2.1.2 向量的几何表示
2.1.2 向量的几何表示
向量与数量的定义
向量与数量的区别
01
回顾复习
定义
向量
数学中,把既有大小,又有方向的量叫做向量。
数量
数学中,把只有大小,没有方向的量叫做数量。
区别
向量
向量不仅有大小还有方向 ,具有双重性,不能比较大小。
数量
数量只有大小,是一个代数量,可以进行代数运算、比较大小。
向量的几何表示
02
学习新知
零向量、单位向量、平行向量概念
阅读课本75页并探究以下问题
有向线段的概念及其三要素
零向量、单位向量、平行向量的定义
01
02
03
向量的表示方法
向量的几何表示
对于向量,我们常用带箭头的线段来表示。
线段按照按一定比例(标度)画出,
它的长度表示向量的大小;
箭头的指向表示向量的方向。
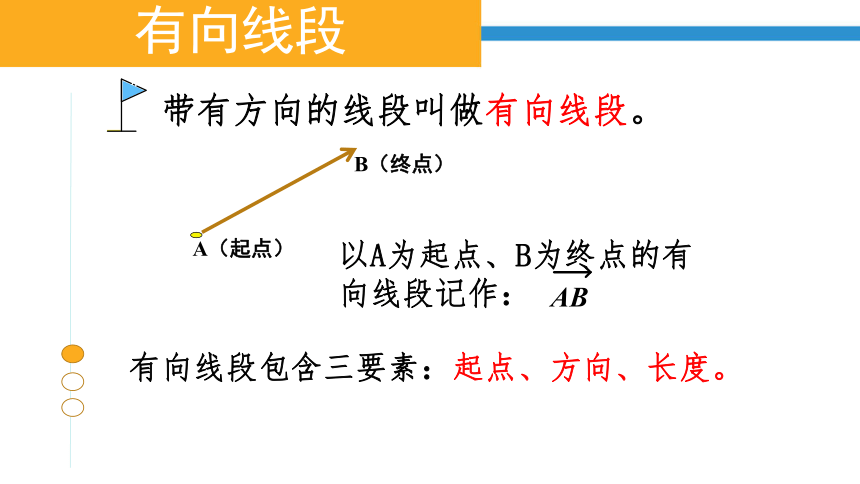
有向线段
带有方向的线段叫做有向线段。
有向线段包含三要素:起点、方向、长度。
A(起点)
B(终点)
以A为起点、B为终点的有向线段记作:
向量的几何表示
向量的几何表示:
向量可以用有向线段表示。
向量也可以用 、 、 …表示;或用有向线
段的起点和终点字母表示,例如 。
c
a
b
最先使用有向线段表示向量的是英国大科学家牛顿。
向量的字母表示:
练一练
一、已知向量 如图所示,下列说法不正确的是( )?
解析:由向量的表示知,A,B,C正确,D不正确.
D
合作探究: “向量就是有向线段,有向线段就是向量.”的说法对吗?
向量与有向线段的区别:
(1)向量只有大小和方向两个要素,与起点无关。(2)有向线段有起点、大小和方向三个素,起点不同,尽管大小和方向相同,也是不同的有向线段。
零向量、单位向量及向量的模
向量 的大小,也就是向量 的长度(或称模),
记作:| | 。
长度为0的向量叫零向量,记作0。 0的方
向是任意的。
长度等于1个单位的向量, 叫单位向量。
平行向量
c
b
a
记作:a∥b
a
记作:a∥c
方向相同或相反的非零向量叫平行向量;
我们规定:零向量与任一向量平行,即
对于任意的向量 ,都有 0∥ 。
a
a
合作探究
【例1】 下列说法正确的是( )
A.数轴是向量
B.方向不同的向量不能比较大小,但同向的向量可以比较大小
C.单位向量的模都相等
D.零向量是没有方向的
解析:数轴没有大小,故不是向量,A不正确;不管向量的方向如何,它们都不能比较大小,故B不正确;单位向量的模都是1,故C正确;零向量的方向是任意的,故D不正确.
C
合作探究
【例2】给出下列说法:
①②
03
随堂练习
练一练
二、 判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
3.若|a| > |b| ,则 a > b.
( )
1.温度含零上和零下温度,所以温度是向量.( )
2.向量的模是一个正实数.( )
×
×
×
注:向量不能比较大小。
4.零向量只有大小没有方向.( )
×
5.单位向量都平行. ( )
×
三、 下列说法中正确的是( )?
A.数量可以比较大小,向量也可以比较大小
B.向量的模可以比较大小
C.模为1的向量都是平行向量
D.由于零向量的方向不确定,故零向量不能与任意向量平行
解析:向量不能比较大小,故A不正确;向量的模是一个数量,可以比较大小,故B正确;平行向量的方向相同或相反,与模无关,故C不正确;规定零向量与任意向量平行,故D不正确.
B
练一练
2
向量的几何表示方法
04
课堂小结
1
零向量、单位向量、平行向量概念。
①用有向线段表示;
②用字母a、b(黑体,印刷用)…表示;
③用有向线段的起点与终点字母。
课本77页 习题2.1A组:1、5.
05
课后作业
阅读课本78页《向量及向量符号的由来》
THANKS
人教A版高中数学必修4
课题:2.1.2 向量的几何表示
2.1.2 向量的几何表示
向量与数量的定义
向量与数量的区别
01
回顾复习
定义
向量
数学中,把既有大小,又有方向的量叫做向量。
数量
数学中,把只有大小,没有方向的量叫做数量。
区别
向量
向量不仅有大小还有方向 ,具有双重性,不能比较大小。
数量
数量只有大小,是一个代数量,可以进行代数运算、比较大小。
向量的几何表示
02
学习新知
零向量、单位向量、平行向量概念
阅读课本75页并探究以下问题
有向线段的概念及其三要素
零向量、单位向量、平行向量的定义
01
02
03
向量的表示方法
向量的几何表示
对于向量,我们常用带箭头的线段来表示。
线段按照按一定比例(标度)画出,
它的长度表示向量的大小;
箭头的指向表示向量的方向。
有向线段
带有方向的线段叫做有向线段。
有向线段包含三要素:起点、方向、长度。
A(起点)
B(终点)
以A为起点、B为终点的有向线段记作:
向量的几何表示
向量的几何表示:
向量可以用有向线段表示。
向量也可以用 、 、 …表示;或用有向线
段的起点和终点字母表示,例如 。
c
a
b
最先使用有向线段表示向量的是英国大科学家牛顿。
向量的字母表示:
练一练
一、已知向量 如图所示,下列说法不正确的是( )?
解析:由向量的表示知,A,B,C正确,D不正确.
D
合作探究: “向量就是有向线段,有向线段就是向量.”的说法对吗?
向量与有向线段的区别:
(1)向量只有大小和方向两个要素,与起点无关。(2)有向线段有起点、大小和方向三个素,起点不同,尽管大小和方向相同,也是不同的有向线段。
零向量、单位向量及向量的模
向量 的大小,也就是向量 的长度(或称模),
记作:| | 。
长度为0的向量叫零向量,记作0。 0的方
向是任意的。
长度等于1个单位的向量, 叫单位向量。
平行向量
c
b
a
记作:a∥b
a
记作:a∥c
方向相同或相反的非零向量叫平行向量;
我们规定:零向量与任一向量平行,即
对于任意的向量 ,都有 0∥ 。
a
a
合作探究
【例1】 下列说法正确的是( )
A.数轴是向量
B.方向不同的向量不能比较大小,但同向的向量可以比较大小
C.单位向量的模都相等
D.零向量是没有方向的
解析:数轴没有大小,故不是向量,A不正确;不管向量的方向如何,它们都不能比较大小,故B不正确;单位向量的模都是1,故C正确;零向量的方向是任意的,故D不正确.
C
合作探究
【例2】给出下列说法:
①②
03
随堂练习
练一练
二、 判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
3.若|a| > |b| ,则 a > b.
( )
1.温度含零上和零下温度,所以温度是向量.( )
2.向量的模是一个正实数.( )
×
×
×
注:向量不能比较大小。
4.零向量只有大小没有方向.( )
×
5.单位向量都平行. ( )
×
三、 下列说法中正确的是( )?
A.数量可以比较大小,向量也可以比较大小
B.向量的模可以比较大小
C.模为1的向量都是平行向量
D.由于零向量的方向不确定,故零向量不能与任意向量平行
解析:向量不能比较大小,故A不正确;向量的模是一个数量,可以比较大小,故B正确;平行向量的方向相同或相反,与模无关,故C不正确;规定零向量与任意向量平行,故D不正确.
B
练一练
2
向量的几何表示方法
04
课堂小结
1
零向量、单位向量、平行向量概念。
①用有向线段表示;
②用字母a、b(黑体,印刷用)…表示;
③用有向线段的起点与终点字母。
课本77页 习题2.1A组:1、5.
05
课后作业
阅读课本78页《向量及向量符号的由来》
THANKS
