2.1.3 相等向量与共线向量 课件 19张PPT
文档属性
| 名称 | 2.1.3 相等向量与共线向量 课件 19张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 11:28:36 | ||
图片预览





文档简介
(共19张PPT)
2.1.3相等向量与共线向量
人教A版必修四
1.向量与数量有什么联系和区别?向量有哪几种表示?
联系:向量与数量都是有大小的量;
区别:向量有方向且不能比较大小,数量无方向且能比较大小.
向量可以用有向线段的起点和终点字母表示,如
也可以用字母 …表示.
知识回顾
2.什么叫向量的模?零向量和单位向量分别是什么概念?
向量的模:向量的大小,也就是向量的长度..
零向量:模为0的向量.
单位向量:模为1个单位长度的向量.
方向任意
3.什么是平行向量?
方向相同或相反的非零向量叫平行向量
规定:零向量与任一向量平行
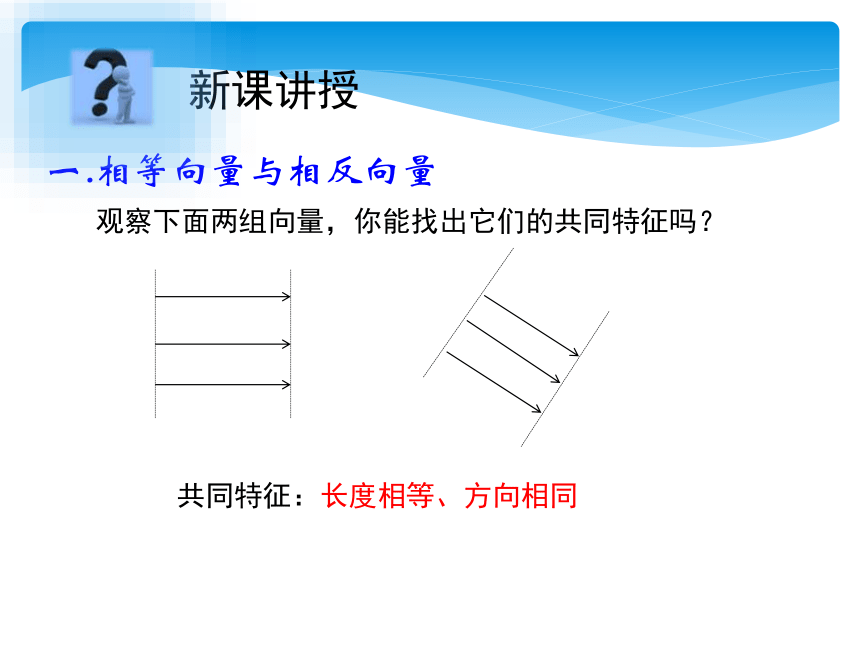
一.相等向量与相反向量
观察下面两组向量,你能找出它们的共同特征吗?
共同特征:长度相等、方向相同
新课讲授
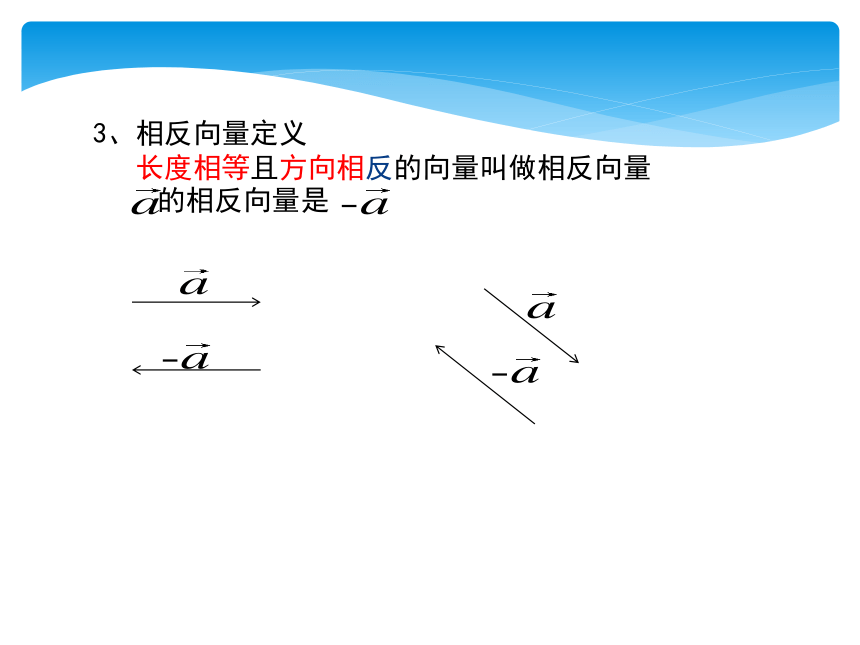
1、相等向量定义
长度相等且方向相同的向量叫做相等向量
记作
2、几点注意
(1)任意两个相等的非零向量,都可以用
同一条有向线段来表示,并且与有向线段的起点无关
(2)平面上两个长度相等且指向一致的有向线段表示
同一个向量,因为向量完全由它的方向和模确定
(3)一个向量在平面内平行移动,所得向量仍与原向量相等,
因此向量可以自由平行移动
二.平行向量与共线向量
思考1:如果两个向量所在的直线互相平行,那么这两个向量的方向有什么关系?
方向相同或相反
不一定
思考3:如图, 是一组平行向量,直线 与 平行,你能在 上任取一点O作为起点,把 移动到直线 上吗?
例2. 判断:
(1) 不相等的向量是否一定不平行?
(2) 与零向量相等的向量必定是什么向量?
(3) 两个非零向量相等的条件是什么?
(4) 共线向量一定在同一直线上吗?
例2. 判断:
(1) 不相等的向量是否一定不平行?
(2) 与零向量相等的向量必定是什么向量?
(3) 两个非零向量相等的条件是什么?
(4) 共线向量一定在同一直线上吗?
不一定
不一定
零向量
长度相等且方向相同
C
练习
1.判断下列命题是否正确,若不正确,请简述理由.
⑤一个向量方向不确定当且仅当模为0;
⑥共线的向量,若起点不同,则终点一定不同.
课堂检测
长度相等且方向相同的向量叫相等向量.
说明:
a
b
c
(3) 任意两个相等的非零向量,都可用同一条有向线段表示,并且与有向线段的起点无关.
(2) 零向量与零向量相等;
课堂总结
共线向量与平行向量关系:
平行向量就是共线向量,因为任一组平行向量都可移到同
一直线上(与有向线段的起点无关).
说明:
(1) 平行向量可以在同一直线上,要区别于两平行线的位置关系;
(2) 共线向量所在直线可以相互平行,要区别于在同一直线上的线段的位置关系.
作业
2.1.3相等向量与共线向量
人教A版必修四
1.向量与数量有什么联系和区别?向量有哪几种表示?
联系:向量与数量都是有大小的量;
区别:向量有方向且不能比较大小,数量无方向且能比较大小.
向量可以用有向线段的起点和终点字母表示,如
也可以用字母 …表示.
知识回顾
2.什么叫向量的模?零向量和单位向量分别是什么概念?
向量的模:向量的大小,也就是向量的长度..
零向量:模为0的向量.
单位向量:模为1个单位长度的向量.
方向任意
3.什么是平行向量?
方向相同或相反的非零向量叫平行向量
规定:零向量与任一向量平行
一.相等向量与相反向量
观察下面两组向量,你能找出它们的共同特征吗?
共同特征:长度相等、方向相同
新课讲授
1、相等向量定义
长度相等且方向相同的向量叫做相等向量
记作
2、几点注意
(1)任意两个相等的非零向量,都可以用
同一条有向线段来表示,并且与有向线段的起点无关
(2)平面上两个长度相等且指向一致的有向线段表示
同一个向量,因为向量完全由它的方向和模确定
(3)一个向量在平面内平行移动,所得向量仍与原向量相等,
因此向量可以自由平行移动
二.平行向量与共线向量
思考1:如果两个向量所在的直线互相平行,那么这两个向量的方向有什么关系?
方向相同或相反
不一定
思考3:如图, 是一组平行向量,直线 与 平行,你能在 上任取一点O作为起点,把 移动到直线 上吗?
例2. 判断:
(1) 不相等的向量是否一定不平行?
(2) 与零向量相等的向量必定是什么向量?
(3) 两个非零向量相等的条件是什么?
(4) 共线向量一定在同一直线上吗?
例2. 判断:
(1) 不相等的向量是否一定不平行?
(2) 与零向量相等的向量必定是什么向量?
(3) 两个非零向量相等的条件是什么?
(4) 共线向量一定在同一直线上吗?
不一定
不一定
零向量
长度相等且方向相同
C
练习
1.判断下列命题是否正确,若不正确,请简述理由.
⑤一个向量方向不确定当且仅当模为0;
⑥共线的向量,若起点不同,则终点一定不同.
课堂检测
长度相等且方向相同的向量叫相等向量.
说明:
a
b
c
(3) 任意两个相等的非零向量,都可用同一条有向线段表示,并且与有向线段的起点无关.
(2) 零向量与零向量相等;
课堂总结
共线向量与平行向量关系:
平行向量就是共线向量,因为任一组平行向量都可移到同
一直线上(与有向线段的起点无关).
说明:
(1) 平行向量可以在同一直线上,要区别于两平行线的位置关系;
(2) 共线向量所在直线可以相互平行,要区别于在同一直线上的线段的位置关系.
作业
