2.1.3 相等向量与共线向量 课件 20张PPT
文档属性
| 名称 | 2.1.3 相等向量与共线向量 课件 20张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 15:52:09 | ||
图片预览






文档简介
(共20张PPT)
2.2.3 向量数乘运算
及其几何意义
高一人教A版必修4新授课
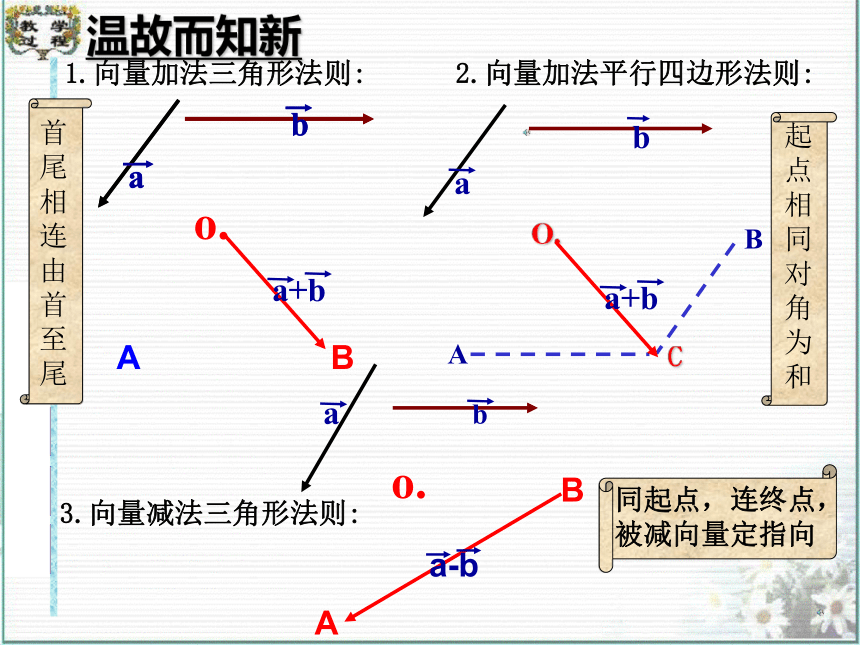
温故而知新
B
A
o.
O.
A
B
1.向量加法三角形法则:
2.向量加法平行四边形法则:
o.
B
A
3.向量减法三角形法则:
1.掌握实数与向量的积的定义、运算律,
并进行有关计算。
明目标
2.向量共线定理的探究及其应用。
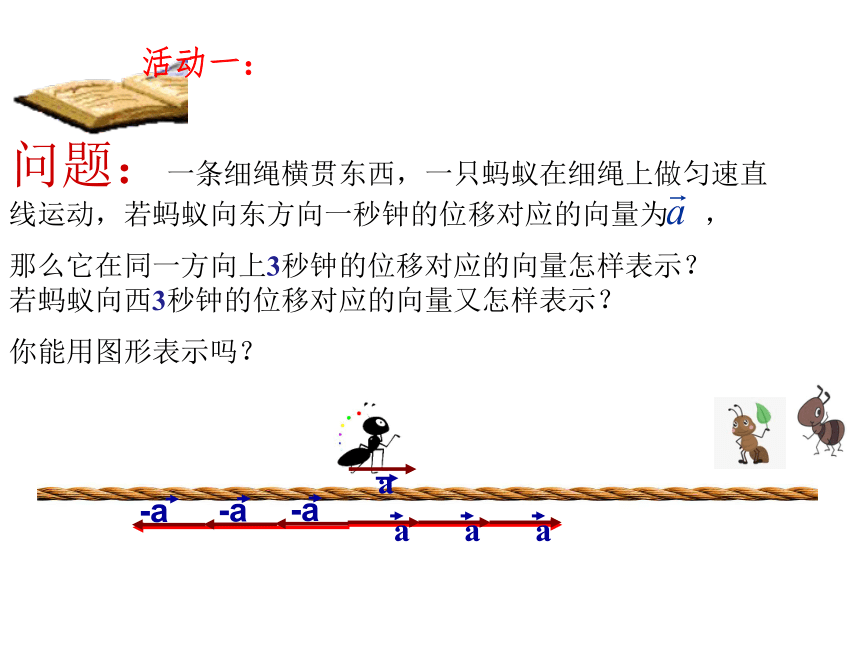
活动一:
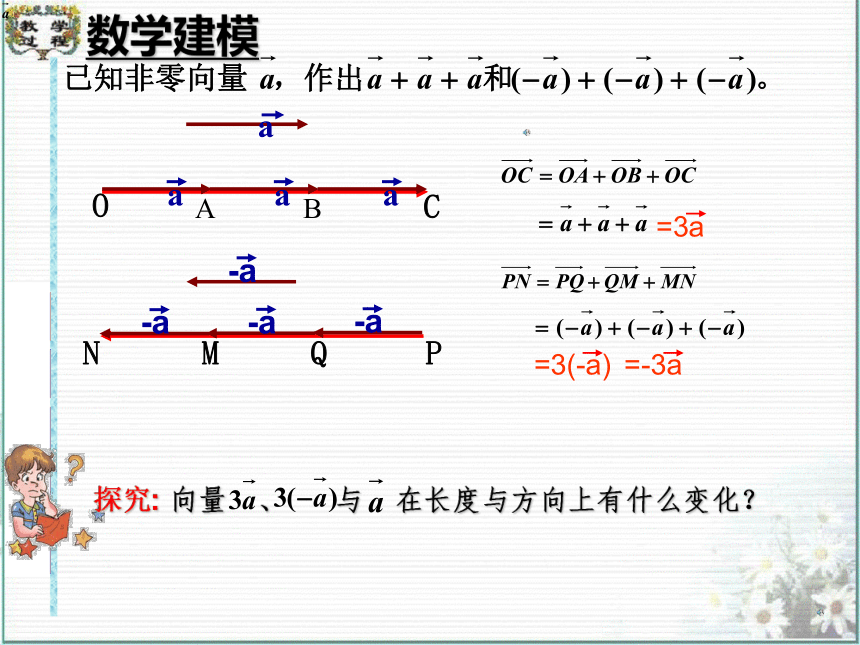
数学建模
一、向量的数乘定义
实数与向量的数乘的运算律:
(1)已知向量 ( ),求作向量3(2 )和(6 ) ,并比较。
活动二:作图总结
(2) 已知向量 ( ),求作向量 和 ,并比较。
(3) 已知向量 ,求作向量 和 ,并比较。
实数与向量的数乘的运算律:
(1) 根据定义,求作向量3(2 )和(6 ) ( ≠ ),并比较。
实数与向量的数乘的运算律:
实数与向量的数乘的运算律:
(3) 已知向量 ,求作向量 和 ,并比较。
实践出真知
结合律
第一分配律
第二分配律
解: (1) 原式 =
(2) 原式 =
(3) 原式 =
计算:(抢答)
(1) (-3)×4 a
(2) 3( a+b) –2( a-b)-a
(3) (2a+3b-c) –(3a-2b+c )
牛刀小试
数乘向量与原向量之间的位置有什么关系?
成立
活动三:
向量共线定理:
自主探究
K=6
各显身手
例1:如图,点C在线段AB上,且AC=5,BC=2,
A
B
C
则有
定理应用
证明:
摇身一变
例2:
定理应用
证明:
摇身再变
例2:
定理应用
二、定理的应用:
1. 证明 向量共线
2. 证明 三点共线: AB=λBC
且有公共点B
3. 证明 两直线平行:
AB=λCD
AB与CD不在同一直线上
直线AB∥直线CD
小结:
A,B,C三点共线
AB∥CD
几何问题
向量化
教材P91,A组9—13题
(选做)B组3、4、5
课后思考:
心动 不如行动
2.2.3 向量数乘运算
及其几何意义
高一人教A版必修4新授课
温故而知新
B
A
o.
O.
A
B
1.向量加法三角形法则:
2.向量加法平行四边形法则:
o.
B
A
3.向量减法三角形法则:
1.掌握实数与向量的积的定义、运算律,
并进行有关计算。
明目标
2.向量共线定理的探究及其应用。
活动一:
数学建模
一、向量的数乘定义
实数与向量的数乘的运算律:
(1)已知向量 ( ),求作向量3(2 )和(6 ) ,并比较。
活动二:作图总结
(2) 已知向量 ( ),求作向量 和 ,并比较。
(3) 已知向量 ,求作向量 和 ,并比较。
实数与向量的数乘的运算律:
(1) 根据定义,求作向量3(2 )和(6 ) ( ≠ ),并比较。
实数与向量的数乘的运算律:
实数与向量的数乘的运算律:
(3) 已知向量 ,求作向量 和 ,并比较。
实践出真知
结合律
第一分配律
第二分配律
解: (1) 原式 =
(2) 原式 =
(3) 原式 =
计算:(抢答)
(1) (-3)×4 a
(2) 3( a+b) –2( a-b)-a
(3) (2a+3b-c) –(3a-2b+c )
牛刀小试
数乘向量与原向量之间的位置有什么关系?
成立
活动三:
向量共线定理:
自主探究
K=6
各显身手
例1:如图,点C在线段AB上,且AC=5,BC=2,
A
B
C
则有
定理应用
证明:
摇身一变
例2:
定理应用
证明:
摇身再变
例2:
定理应用
二、定理的应用:
1. 证明 向量共线
2. 证明 三点共线: AB=λBC
且有公共点B
3. 证明 两直线平行:
AB=λCD
AB与CD不在同一直线上
直线AB∥直线CD
小结:
A,B,C三点共线
AB∥CD
几何问题
向量化
教材P91,A组9—13题
(选做)B组3、4、5
课后思考:
心动 不如行动
