2.1 平面向量的实际背景及基本概念 课件 22张PPT
文档属性
| 名称 | 2.1 平面向量的实际背景及基本概念 课件 22张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 16:08:35 | ||
图片预览






文档简介
(共22张PPT)
§2.1平面向量的实际背景 及基本概念
——向量及向量符号的由来
阅读与思考:向量及向量符号的由来
阅读与思考:向量及向量符号的由来
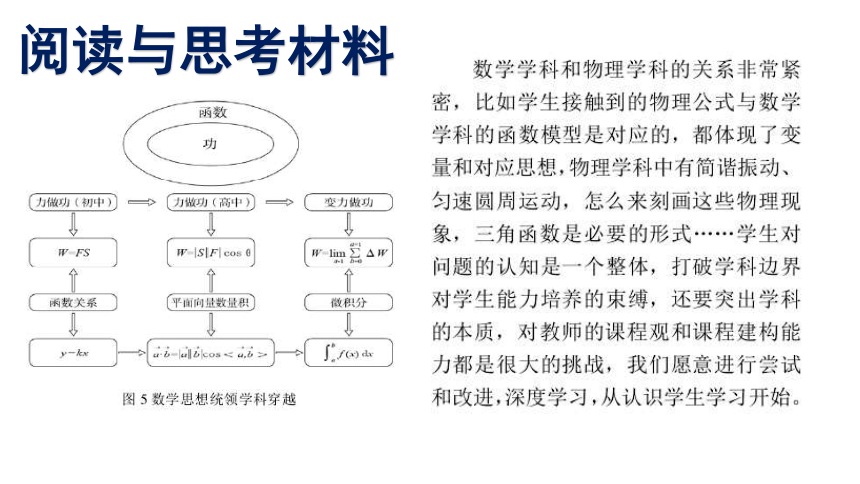
阅读与思考材料
阅读与思考材料
阅读与思考材料
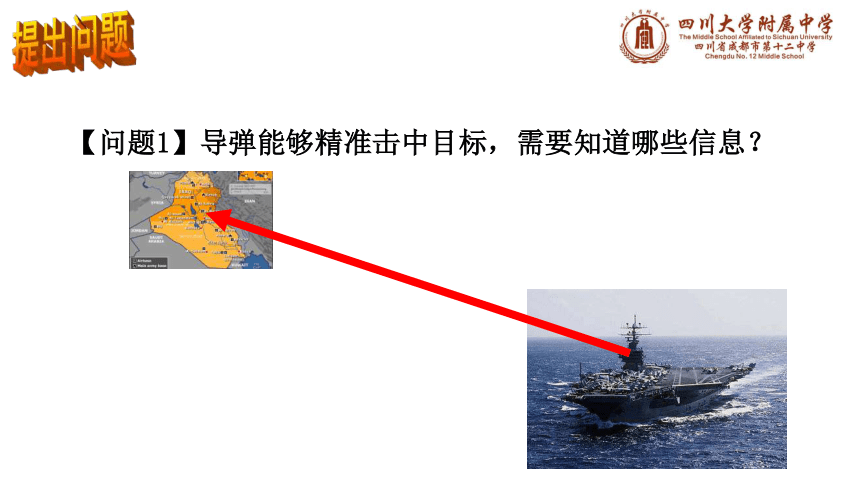
【问题1】导弹能够精准击中目标,需要知道哪些信息?
【问题2】能否再举出一些既有大小又有方向的量?
向 量
1. 向量的定义
向量:既有大小又有方向的量叫做向量.
向量的两要素: 大小 方向
1.温度含零上和零下温度,所以温度是向量.
2.坐标平面上的x轴和y轴都是向量.
辨析
(模)
3.给出下列物理量:①质量;②速度;③位移;④力;
⑤路程;⑥功;⑦加速度.其中是向量的有 .
基于实际背景,理解并掌握向量的基本概念。
核心问题
请同学们按下列要求画出力的图示,并讨论如何表示向量?
4N的重力
1N的浮力
(1)几何表示:向量常用有向线段(带箭头的线段)表示。 有向线段的长度表示向量的大小(模); 箭头所指的方向表示向量的方向。 有向线段的三个要素:起点、方向、长度
2. 向量的表示
B(终点)
A(起点)
印刷用黑体
(3)向量的模:有向线段AB的长度记作:
(读为模,而非绝对值);
学会了向量的表示,就可以直观去研究它,自然可以想到从特殊入手,下面我们来观察向量模的变化:
长度为1的向量
1
0
2
3
【问题3】能给它取个名字吗?
我们来观察向量模的变化:
(1)单位向量:长度为1的向量;
(2)零向量:长度为0的向量,记作 ;
规定:零向量的方向是任意的.
0
1
2
3
3.两个特殊的向量
【问题4】
零向量的
方向呢?
思考:刚才我们已经了解了向量大小上的特殊情况,下面我们从方向上来探究向量间的特殊关系
如图,设O是边长为1的正六边形ABCDEF的中心,
(1)给图中的部分线段加上箭头表示向量,并写出你所表示的向量;
(2)相互讨论:这些向量有哪些关系?
O
A
B
C
D
E
F
4.向量间的特殊关系
(1)平行向量
①方向相同或相反的非零向量叫平行向量;
O
A
B
C
D
E
F
记为 .
辨析
×
4.向量间的特殊关系
(2)相等向量
长度相等且方向相同的向量叫相等向量。
O
A
B
C
D
E
F
说明:任意两个相等的非零向量,都可用同一条有向线段来表示,并且与有向线段的起点无关。
辨析
√
数学研究的是:自由向量!!!
【问题5】向量平移后发生变化了吗?
4.向量间的特殊关系
平行向量就是共线向量,
共线向量就是平行向量!
O
A
B
C
D
E
F
【问题6】把右图中的三个平行
向量的起点都平移到 处,那么
它们终点的位置有何特征呢?
A
D
F
(3)共线向量与平行向量的关系
向量的自由可移性!!!
【问题7】平行向量与平行线段的区别与联系。
根据下列小题的条件,分别判断四边形ABCD的形状:
(1) ; (2) 且
(1)四边形ABCD是平行四边形。
(2)四边形ABCD是菱形。
辨析
从同类具体事例中抽象出共同本质特征
下定义
符号表示
认识特殊对象
考察特殊关系
1.知识
2.学习新概念的基本思路
本节课学习了哪些新的概念?
思考:“数”有运算和运算律,“向量”呢?
已知飞机从A地按北偏东方向飞行2000km到达B地,再从B地按南偏东 方向飞行2000km到达C地,最后从C地按西南方向飞行了 km到达D地。画图表示向量 ,并指出向量 的模和方向。
1.小黄P129
人生不仅仅取决于努力的程度,
更重要的是努力的方向!
§2.1平面向量的实际背景 及基本概念
——向量及向量符号的由来
阅读与思考:向量及向量符号的由来
阅读与思考:向量及向量符号的由来
阅读与思考材料
阅读与思考材料
阅读与思考材料
【问题1】导弹能够精准击中目标,需要知道哪些信息?
【问题2】能否再举出一些既有大小又有方向的量?
向 量
1. 向量的定义
向量:既有大小又有方向的量叫做向量.
向量的两要素: 大小 方向
1.温度含零上和零下温度,所以温度是向量.
2.坐标平面上的x轴和y轴都是向量.
辨析
(模)
3.给出下列物理量:①质量;②速度;③位移;④力;
⑤路程;⑥功;⑦加速度.其中是向量的有 .
基于实际背景,理解并掌握向量的基本概念。
核心问题
请同学们按下列要求画出力的图示,并讨论如何表示向量?
4N的重力
1N的浮力
(1)几何表示:向量常用有向线段(带箭头的线段)表示。 有向线段的长度表示向量的大小(模); 箭头所指的方向表示向量的方向。 有向线段的三个要素:起点、方向、长度
2. 向量的表示
B(终点)
A(起点)
印刷用黑体
(3)向量的模:有向线段AB的长度记作:
(读为模,而非绝对值);
学会了向量的表示,就可以直观去研究它,自然可以想到从特殊入手,下面我们来观察向量模的变化:
长度为1的向量
1
0
2
3
【问题3】能给它取个名字吗?
我们来观察向量模的变化:
(1)单位向量:长度为1的向量;
(2)零向量:长度为0的向量,记作 ;
规定:零向量的方向是任意的.
0
1
2
3
3.两个特殊的向量
【问题4】
零向量的
方向呢?
思考:刚才我们已经了解了向量大小上的特殊情况,下面我们从方向上来探究向量间的特殊关系
如图,设O是边长为1的正六边形ABCDEF的中心,
(1)给图中的部分线段加上箭头表示向量,并写出你所表示的向量;
(2)相互讨论:这些向量有哪些关系?
O
A
B
C
D
E
F
4.向量间的特殊关系
(1)平行向量
①方向相同或相反的非零向量叫平行向量;
O
A
B
C
D
E
F
记为 .
辨析
×
4.向量间的特殊关系
(2)相等向量
长度相等且方向相同的向量叫相等向量。
O
A
B
C
D
E
F
说明:任意两个相等的非零向量,都可用同一条有向线段来表示,并且与有向线段的起点无关。
辨析
√
数学研究的是:自由向量!!!
【问题5】向量平移后发生变化了吗?
4.向量间的特殊关系
平行向量就是共线向量,
共线向量就是平行向量!
O
A
B
C
D
E
F
【问题6】把右图中的三个平行
向量的起点都平移到 处,那么
它们终点的位置有何特征呢?
A
D
F
(3)共线向量与平行向量的关系
向量的自由可移性!!!
【问题7】平行向量与平行线段的区别与联系。
根据下列小题的条件,分别判断四边形ABCD的形状:
(1) ; (2) 且
(1)四边形ABCD是平行四边形。
(2)四边形ABCD是菱形。
辨析
从同类具体事例中抽象出共同本质特征
下定义
符号表示
认识特殊对象
考察特殊关系
1.知识
2.学习新概念的基本思路
本节课学习了哪些新的概念?
思考:“数”有运算和运算律,“向量”呢?
已知飞机从A地按北偏东方向飞行2000km到达B地,再从B地按南偏东 方向飞行2000km到达C地,最后从C地按西南方向飞行了 km到达D地。画图表示向量 ,并指出向量 的模和方向。
1.小黄P129
人生不仅仅取决于努力的程度,
更重要的是努力的方向!
