3.4 基本不等式 第一课时课件 28张PPT
文档属性
| 名称 | 3.4 基本不等式 第一课时课件 28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 11:24:51 | ||
图片预览






文档简介
(共28张PPT)
3.4 基本不等式:(第一课时)
国际数学家大会是由国际数学联盟(IMU)主办,首届大会于1897年在瑞士苏黎士举行,1900年巴黎大会之后每四年举行一次,它已经成为最高水平的全球性数学科学学术会议.
有哪位同学知道哪一届国际数学家大会在北京举行,它的会标是什么?
第24届国际数学家大会
会标是根据中国古代
数学家赵爽的弦图设计的,
颜色的明暗使它看上去像
一个风车,代表中国人民
热情好客.
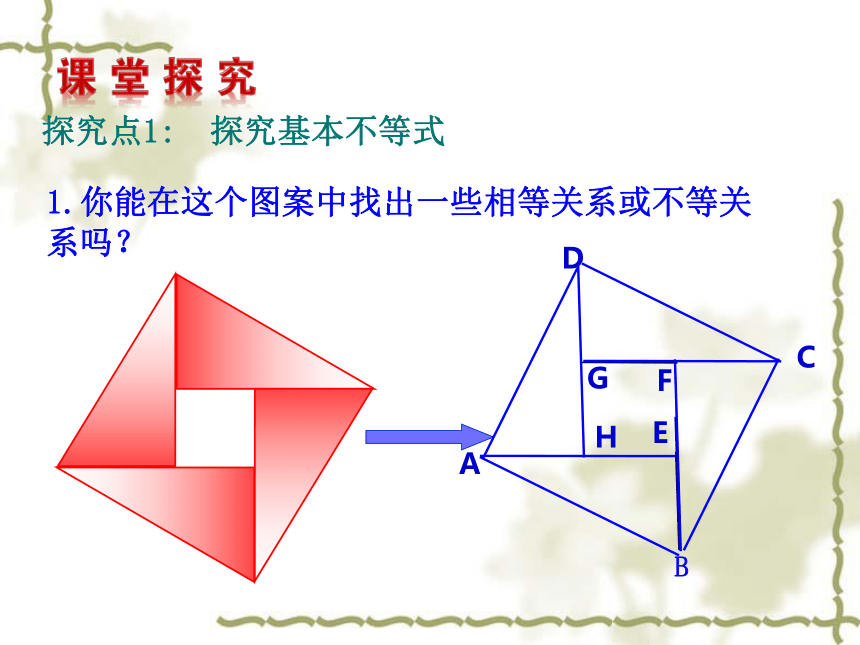
1.你能在这个图案中找出一些相等关系或不等关系吗?
探究点1: 探究基本不等式
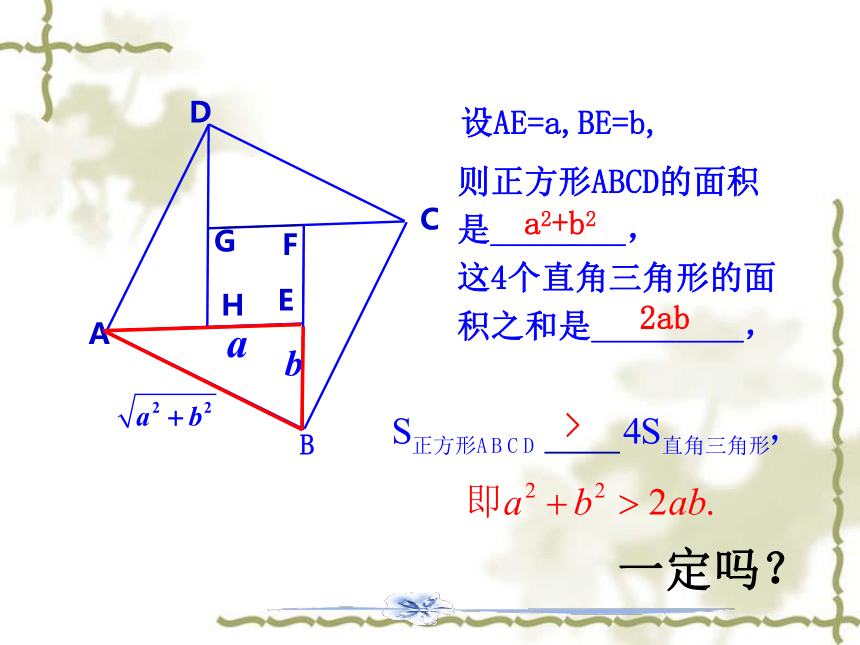
则正方形ABCD的面积
是________,
这4个直角三角形的面积之和是_________,
设AE=a,BE=b,
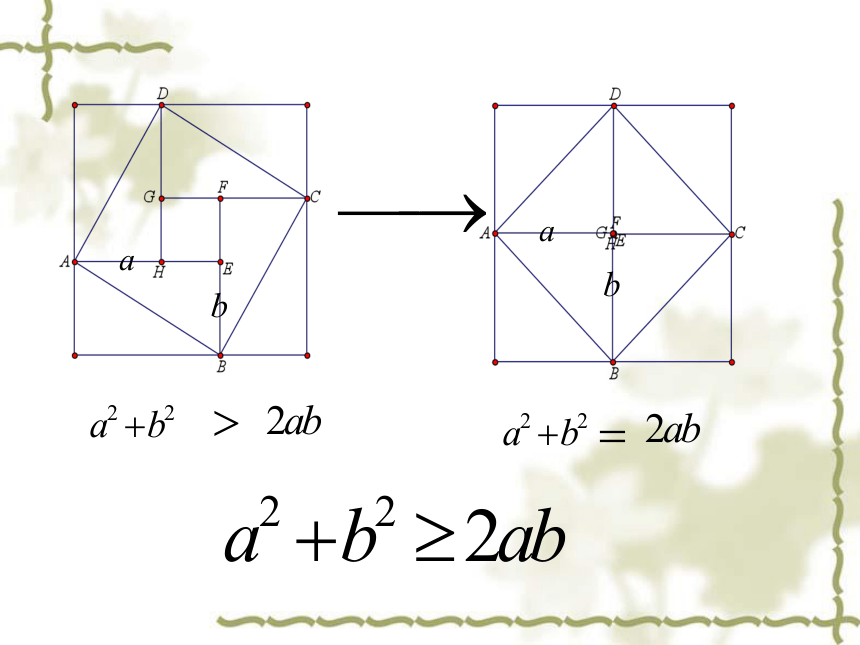
a2+b2
2ab
>
一定吗?
一般地,对于任意实数a,b,我们有:
当且仅当a=b时,等号成立.
3.你能给出它的证明吗?
【提升总结】
4.你能用不等式的性质直接推导吗?
通常我们把上式写作
证明:要证
只要证
①
要证①,只要证
②
要证②,只要证
③
显然, ③是成立的.当且仅当a=b时, ③中的等号成立.
基本不等式:
注意:(1)a,b均为正数;
(2)当且仅当a=b时取等号.
【提升总结】
你能用这个图得出基本不等式的几何解释吗?
A
B
C
D
E
a
b
O
如图, AB是圆的直径, O为圆心,点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
②如何用a, b表示CD? CD=______
①如何用a, b表示OD? OD=______
半弦CD小于或等于圆的半径.
用不等式表示为
几何意义(解释):半弦不大于半径.
O
C
D
A
B
(半径不小于半弦)
上述不等式当且仅当点C与圆心重合,
即当a=b时,等号成立.
可以叙述为(代数解释):
两个正数的几何平均数不大于它们的算术平均数.
叫做正数a,b的算术平均数,
叫做正数a,b的几何平均数.
基本不等式:
算
术
平
均
数
2
1
探究点2:基本不等式在求最值中的应用
结论1 两个正数积为定值,则和有最小值.
当xy的值是常数 时,当且仅当x=y时,
x+y有最小值
【提升总结】
(x>0,y >0)
A
例
结论2 两个正数和为定值,则积有最大值.
当x+y的值是常数S 时,当且仅当x=y时,
xy有最大值
【提升总结】
(x>0,y >0)
注意:①各项皆为正数;
②和为定值或积为定值;
③注意等号成立的条件.
“正”,
“定”,
“等”.
结论1 两个正数积为定值,则和有最小值.
结论2 两个正数和为定值,则积有最大值.
归纳:
应用要点:
1
2.在下列函数中,最小值为2的是( )
A. B.
C. D.
C
10
3.已知 且 则 的最大
值为_____.
解:
1.两个重要的不等式
(1)
(2)基本不等式
2.不等式的简单应用:主要是求最值
把握 “六字方针”,即 “一正,二定,三等”.
本节课你能感受到哪些数学思想?
布置作业:
3.4 基本不等式:(第一课时)
国际数学家大会是由国际数学联盟(IMU)主办,首届大会于1897年在瑞士苏黎士举行,1900年巴黎大会之后每四年举行一次,它已经成为最高水平的全球性数学科学学术会议.
有哪位同学知道哪一届国际数学家大会在北京举行,它的会标是什么?
第24届国际数学家大会
会标是根据中国古代
数学家赵爽的弦图设计的,
颜色的明暗使它看上去像
一个风车,代表中国人民
热情好客.
1.你能在这个图案中找出一些相等关系或不等关系吗?
探究点1: 探究基本不等式
则正方形ABCD的面积
是________,
这4个直角三角形的面积之和是_________,
设AE=a,BE=b,
a2+b2
2ab
>
一定吗?
一般地,对于任意实数a,b,我们有:
当且仅当a=b时,等号成立.
3.你能给出它的证明吗?
【提升总结】
4.你能用不等式的性质直接推导吗?
通常我们把上式写作
证明:要证
只要证
①
要证①,只要证
②
要证②,只要证
③
显然, ③是成立的.当且仅当a=b时, ③中的等号成立.
基本不等式:
注意:(1)a,b均为正数;
(2)当且仅当a=b时取等号.
【提升总结】
你能用这个图得出基本不等式的几何解释吗?
A
B
C
D
E
a
b
O
如图, AB是圆的直径, O为圆心,点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
②如何用a, b表示CD? CD=______
①如何用a, b表示OD? OD=______
半弦CD小于或等于圆的半径.
用不等式表示为
几何意义(解释):半弦不大于半径.
O
C
D
A
B
(半径不小于半弦)
上述不等式当且仅当点C与圆心重合,
即当a=b时,等号成立.
可以叙述为(代数解释):
两个正数的几何平均数不大于它们的算术平均数.
叫做正数a,b的算术平均数,
叫做正数a,b的几何平均数.
基本不等式:
算
术
平
均
数
2
1
探究点2:基本不等式在求最值中的应用
结论1 两个正数积为定值,则和有最小值.
当xy的值是常数 时,当且仅当x=y时,
x+y有最小值
【提升总结】
(x>0,y >0)
A
例
结论2 两个正数和为定值,则积有最大值.
当x+y的值是常数S 时,当且仅当x=y时,
xy有最大值
【提升总结】
(x>0,y >0)
注意:①各项皆为正数;
②和为定值或积为定值;
③注意等号成立的条件.
“正”,
“定”,
“等”.
结论1 两个正数积为定值,则和有最小值.
结论2 两个正数和为定值,则积有最大值.
归纳:
应用要点:
1
2.在下列函数中,最小值为2的是( )
A. B.
C. D.
C
10
3.已知 且 则 的最大
值为_____.
解:
1.两个重要的不等式
(1)
(2)基本不等式
2.不等式的简单应用:主要是求最值
把握 “六字方针”,即 “一正,二定,三等”.
本节课你能感受到哪些数学思想?
布置作业:
