4.7 解三角形(一) 正、余弦定理的综合运用 课件 18张PPT
文档属性
| 名称 | 4.7 解三角形(一) 正、余弦定理的综合运用 课件 18张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 564.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 11:30:24 | ||
图片预览






文档简介
(共18张PPT)
4.7 解三角形(一)
正、余弦定理的综合运用
六环节立体引学
版本:人教版
对象:高中三年级
版本:人教版
对象:高中三年级
版本:人教版
版本:
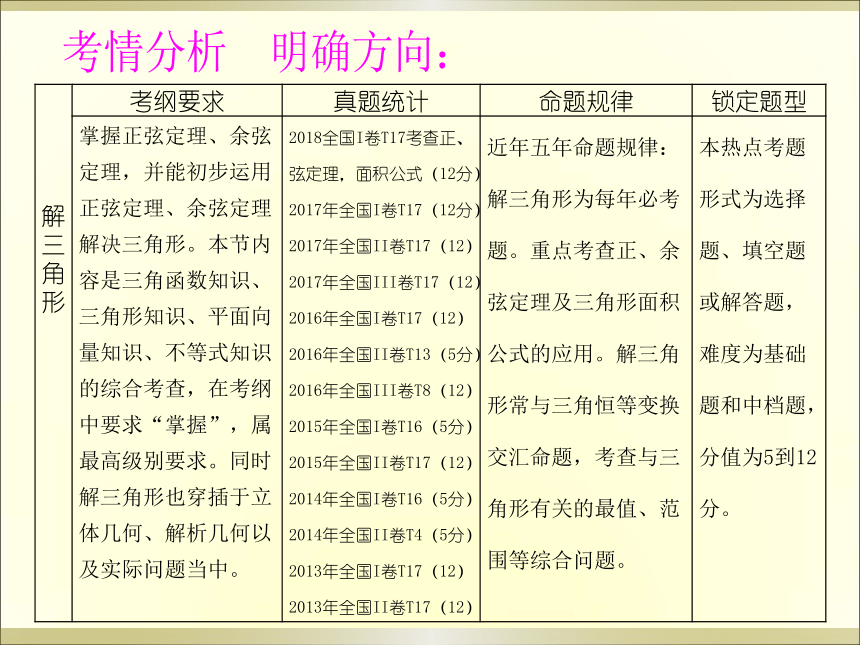
解三角形 考纲要求 真题统计 命题规律 锁定题型
掌握正弦定理、余弦定理,并能初步运用正弦定理、余弦定理解决三角形。本节内容是三角函数知识、三角形知识、平面向量知识、不等式知识的综合考查,在考纲中要求“掌握”,属最高级别要求。同时解三角形也穿插于立体几何、解析几何以及实际问题当中。 2018全国I卷T17考查正、弦定理,面积公式(12分)
2017年全国I卷T17(12分)
2017年全国II卷T17(12)
2017年全国III卷T17(12)
2016年全国I卷T17(12)
2016年全国II卷T13(5分)
2016年全国III卷T8(12)
2015年全国I卷T16(5分)2015年全国II卷T17(12)
2014年全国I卷T16(5分)2014年全国II卷T4(5分)
2013年全国I卷T17(12)
2013年全国II卷T17(12) 近年五年命题规律:解三角形为每年必考题。重点考查正、余弦定理及三角形面积公式的应用。解三角形常与三角恒等变换交汇命题,考查与三角形有关的最值、范围等综合问题。 本热点考题形式为选择题、填空题或解答题,难度为基础题和中档题,分值为5到12分。
点拨:解三角形的基本思想(原理): 解三角形也就是利用三角形内蕴的基本方程与不等式(正弦定理、余弦定理,三角形内角和定理,三角形三边的不等关系),解决代数条件下或几何条件下的三角形三条边与三个角的度量问题。 在获得三角形三条边或三个角的度量关系的同时,也可以获得该三角形其他度量信息,如三角形的周长、面积以及其他伴随要素(高线、角平分线、中线)的度量信息。所谓给定的代数条件或几何条件,既可以是基于三角形三条边、三个角的有关等式,也可以是基于周长、面积等反问题信息.这些给定的条件是否等价于三角形全等判定的基本定理(角边角、边角边、边边边),决定了该三角形是完全可解,还是局部可解。
范例启迪,领司方法
(1)解三角形问题的主要工具就是正弦定理、余弦定理,
(2)简单问题求边或角时应找到条件及所求对象的边角关系,选择适当的定理,列出方程(组)求解
(3)复杂问题可联系条件与结论,将含有边或角的齐次等式利用正弦或余弦定理进行边角互化
(4)对解三角形的题目,可将题目所涉及的条件用图示法标出来,便于找到解题的方法。
学数学的时候
数学在心头
才下眉头
却上心头
想出来,如饮美酒
教数学的时候
数学在口头
深水静流
曲径通幽
讲出来,如展歌喉
写数学的时候
数学在手头
快意百炼钢
化为绕指柔
写出来,如描锦绣
谢谢指导!
4.7 解三角形(一)
正、余弦定理的综合运用
六环节立体引学
版本:人教版
对象:高中三年级
版本:人教版
对象:高中三年级
版本:人教版
版本:
解三角形 考纲要求 真题统计 命题规律 锁定题型
掌握正弦定理、余弦定理,并能初步运用正弦定理、余弦定理解决三角形。本节内容是三角函数知识、三角形知识、平面向量知识、不等式知识的综合考查,在考纲中要求“掌握”,属最高级别要求。同时解三角形也穿插于立体几何、解析几何以及实际问题当中。 2018全国I卷T17考查正、弦定理,面积公式(12分)
2017年全国I卷T17(12分)
2017年全国II卷T17(12)
2017年全国III卷T17(12)
2016年全国I卷T17(12)
2016年全国II卷T13(5分)
2016年全国III卷T8(12)
2015年全国I卷T16(5分)2015年全国II卷T17(12)
2014年全国I卷T16(5分)2014年全国II卷T4(5分)
2013年全国I卷T17(12)
2013年全国II卷T17(12) 近年五年命题规律:解三角形为每年必考题。重点考查正、余弦定理及三角形面积公式的应用。解三角形常与三角恒等变换交汇命题,考查与三角形有关的最值、范围等综合问题。 本热点考题形式为选择题、填空题或解答题,难度为基础题和中档题,分值为5到12分。
点拨:解三角形的基本思想(原理): 解三角形也就是利用三角形内蕴的基本方程与不等式(正弦定理、余弦定理,三角形内角和定理,三角形三边的不等关系),解决代数条件下或几何条件下的三角形三条边与三个角的度量问题。 在获得三角形三条边或三个角的度量关系的同时,也可以获得该三角形其他度量信息,如三角形的周长、面积以及其他伴随要素(高线、角平分线、中线)的度量信息。所谓给定的代数条件或几何条件,既可以是基于三角形三条边、三个角的有关等式,也可以是基于周长、面积等反问题信息.这些给定的条件是否等价于三角形全等判定的基本定理(角边角、边角边、边边边),决定了该三角形是完全可解,还是局部可解。
范例启迪,领司方法
(1)解三角形问题的主要工具就是正弦定理、余弦定理,
(2)简单问题求边或角时应找到条件及所求对象的边角关系,选择适当的定理,列出方程(组)求解
(3)复杂问题可联系条件与结论,将含有边或角的齐次等式利用正弦或余弦定理进行边角互化
(4)对解三角形的题目,可将题目所涉及的条件用图示法标出来,便于找到解题的方法。
学数学的时候
数学在心头
才下眉头
却上心头
想出来,如饮美酒
教数学的时候
数学在口头
深水静流
曲径通幽
讲出来,如展歌喉
写数学的时候
数学在手头
快意百炼钢
化为绕指柔
写出来,如描锦绣
谢谢指导!
