3.3 二元一次不等式(组)与简单的线性规划问题 课件 20张PPT
文档属性
| 名称 | 3.3 二元一次不等式(组)与简单的线性规划问题 课件 20张PPT |
|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
导学引领
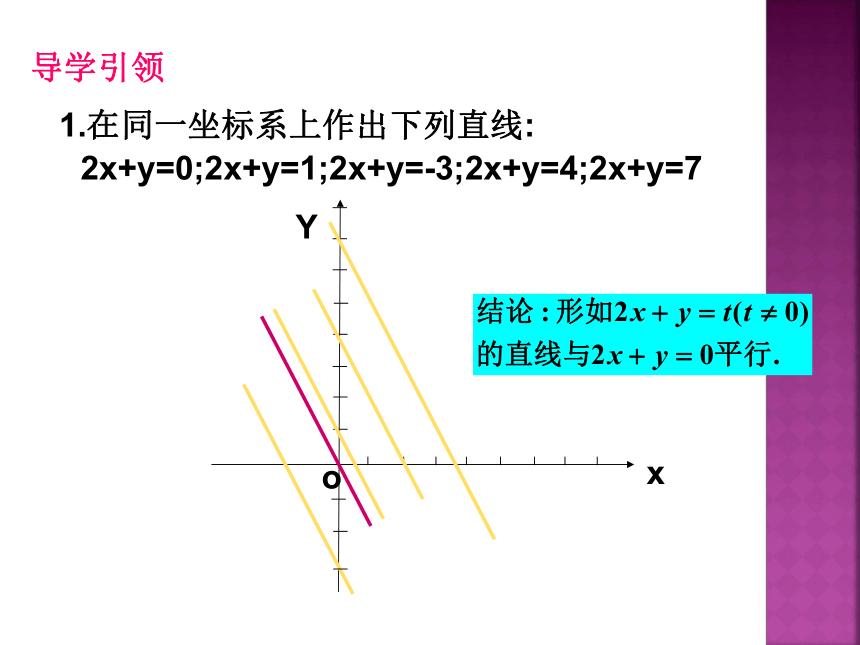
1.在同一坐标系上作出下列直线:
2x+y=0;2x+y=1;2x+y=-3;2x+y=4;2x+y=7
x
Y
o
2.作出下列不等式组的所表示的平面区域
导学引领
y
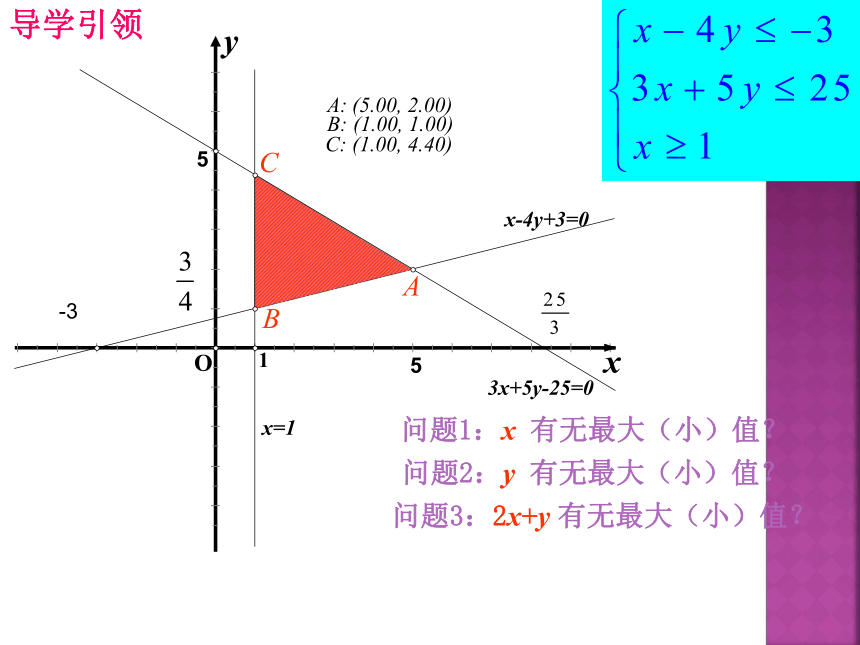
问题1:x 有无最大(小)值?
问题2:y 有无最大(小)值?
问题3:2x+y 有无最大(小)值?
-3
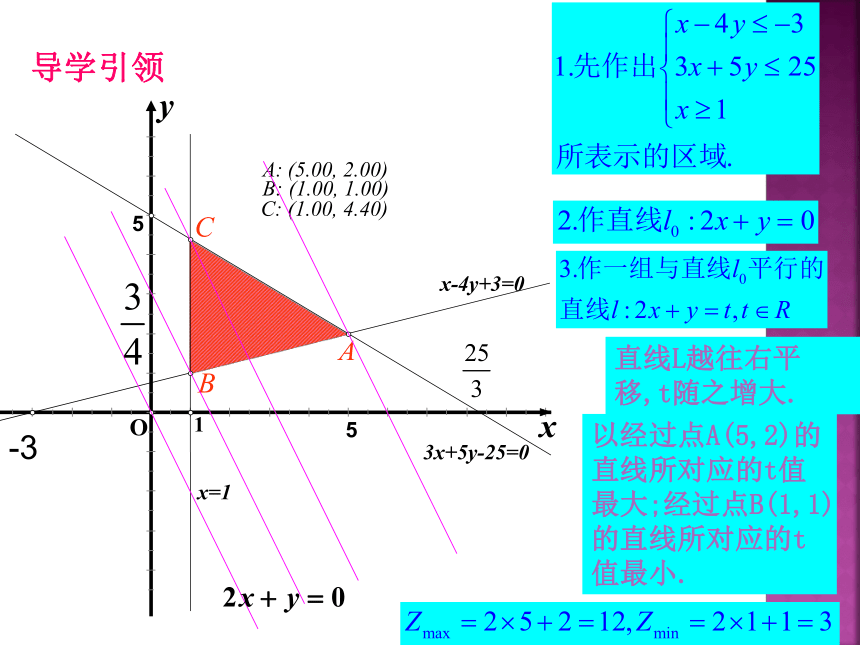
导学引领
把上面两个问题综合起来:
设z=2x+y,求满足
时,求z的最大值和最小值.
导学引领
y
直线L越往右平移,t随之增大.
以经过点A(5,2)的直线所对应的t值最大;经过点B(1,1)的直线所对应的t值最小.
-3
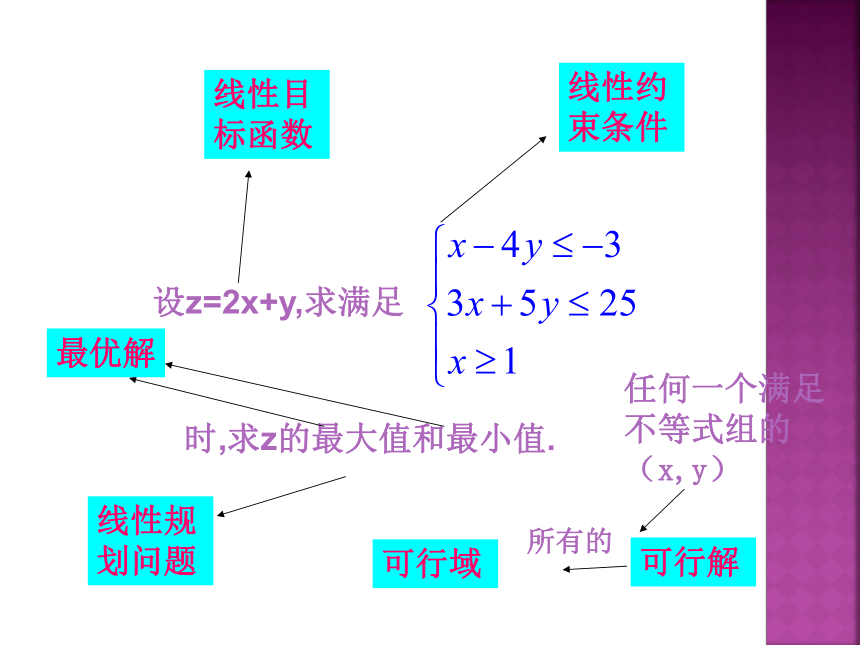
导学引领
线性目标函数
线性约束条件
线性规划问题
任何一个满足不等式组的(x,y)
可行解
可行域
所有的
最优解
概念
1. 由x,y 的不等式(或方程)组成的不等式组称为x,y 的约束条件。关于x,y 的一次不等式或方程组成的不等式组称为x,y 的线性约束条件。
2. 欲达到最大值或最小值所涉及的变量x,y 的解析式称为目标函数。关于x,y 的一次目标函数称为线性目标函数。
3. 求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。
4. 满足线性约束条件的解(x,y)称为可行解。所有可行解组成的集合称为可行域。
5. 使目标函数取得最大值或最小值的可行解称为最优解。
基础问题展示交流
1)求使 的最大值,使x,y满足约束条件
2)求使 的最大值和最小值,使x,y满足约束条件
5
5
1
O
x
y
y-x=0
x+y-1=0
1
-1
y+1=0
A(2,-1)
B(-1,-1)
基础问题展示交流
5
5
1
O
x
y
1
-1
5x+3y=15
X-5y=3
y=x+1
A(-2,-1)
B(3/2,5/2)
-1
3
基础问题展示交流
利用图解法解决线性规划问题的步骤:
画——画出线性约束条件所表示的可行域
答——做出答案
求——根据观察的结论,先求交点的坐标,再求出最优解
移——在目标函数所表示的一组平行线(与目标函数中z=0平行)中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线
例1.要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
规格类型
钢板类型
今需要A ,B,C三种规格的成品分别15,18,27块,
(1)试用数学关系和图形表示上述要求。
(2)各截这两种钢板多少张可得所需A、B、C三种规格成品,且使所用钢板张数最少?
能力提升展示交流
A规格 B规格 C规格
第一种钢板 2 1 1
第二种钢板 1 2 3
解:设需截第一种钢板x张,第二种钢板
y张,设使用钢板的总张数为Z,则
目标函数为 z = x + y
能力提升展示交流
y
x
O
2
2
4
8
8
18
28
16
能力提升展示交流
y
x
O
2
2
4
8
8
18
28
16
能力提升展示交流
y
x
O
2
2
4
8
8
18
28
16
能力提升展示交流
y
x
O
2
2
4
8
8
18
28
16
如何找整数时的最优解?
能力提升展示交流
y
x
O
2
2
4
8
8
18
28
16
如何找整数时的最优解?
能力提升展示交流
1. 建立线性约束条件和线性目标函数; 2.运用图解法,求出最优解;
(实际问题需要整数解时,适当
调整,确定最优解.)
3.转化为实际问题的解,写出答案
解线性规划应用题的一般步骤:
我们一起来总结
导学引领
1.在同一坐标系上作出下列直线:
2x+y=0;2x+y=1;2x+y=-3;2x+y=4;2x+y=7
x
Y
o
2.作出下列不等式组的所表示的平面区域
导学引领
y
问题1:x 有无最大(小)值?
问题2:y 有无最大(小)值?
问题3:2x+y 有无最大(小)值?
-3
导学引领
把上面两个问题综合起来:
设z=2x+y,求满足
时,求z的最大值和最小值.
导学引领
y
直线L越往右平移,t随之增大.
以经过点A(5,2)的直线所对应的t值最大;经过点B(1,1)的直线所对应的t值最小.
-3
导学引领
线性目标函数
线性约束条件
线性规划问题
任何一个满足不等式组的(x,y)
可行解
可行域
所有的
最优解
概念
1. 由x,y 的不等式(或方程)组成的不等式组称为x,y 的约束条件。关于x,y 的一次不等式或方程组成的不等式组称为x,y 的线性约束条件。
2. 欲达到最大值或最小值所涉及的变量x,y 的解析式称为目标函数。关于x,y 的一次目标函数称为线性目标函数。
3. 求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。
4. 满足线性约束条件的解(x,y)称为可行解。所有可行解组成的集合称为可行域。
5. 使目标函数取得最大值或最小值的可行解称为最优解。
基础问题展示交流
1)求使 的最大值,使x,y满足约束条件
2)求使 的最大值和最小值,使x,y满足约束条件
5
5
1
O
x
y
y-x=0
x+y-1=0
1
-1
y+1=0
A(2,-1)
B(-1,-1)
基础问题展示交流
5
5
1
O
x
y
1
-1
5x+3y=15
X-5y=3
y=x+1
A(-2,-1)
B(3/2,5/2)
-1
3
基础问题展示交流
利用图解法解决线性规划问题的步骤:
画——画出线性约束条件所表示的可行域
答——做出答案
求——根据观察的结论,先求交点的坐标,再求出最优解
移——在目标函数所表示的一组平行线(与目标函数中z=0平行)中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线
例1.要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
规格类型
钢板类型
今需要A ,B,C三种规格的成品分别15,18,27块,
(1)试用数学关系和图形表示上述要求。
(2)各截这两种钢板多少张可得所需A、B、C三种规格成品,且使所用钢板张数最少?
能力提升展示交流
A规格 B规格 C规格
第一种钢板 2 1 1
第二种钢板 1 2 3
解:设需截第一种钢板x张,第二种钢板
y张,设使用钢板的总张数为Z,则
目标函数为 z = x + y
能力提升展示交流
y
x
O
2
2
4
8
8
18
28
16
能力提升展示交流
y
x
O
2
2
4
8
8
18
28
16
能力提升展示交流
y
x
O
2
2
4
8
8
18
28
16
能力提升展示交流
y
x
O
2
2
4
8
8
18
28
16
如何找整数时的最优解?
能力提升展示交流
y
x
O
2
2
4
8
8
18
28
16
如何找整数时的最优解?
能力提升展示交流
1. 建立线性约束条件和线性目标函数; 2.运用图解法,求出最优解;
(实际问题需要整数解时,适当
调整,确定最优解.)
3.转化为实际问题的解,写出答案
解线性规划应用题的一般步骤:
我们一起来总结
