高中数学人教新课标A版必修5第三章 不等式 阅读与思考 海伦和秦九韶 课件 20张PPT
文档属性
| 名称 | 高中数学人教新课标A版必修5第三章 不等式 阅读与思考 海伦和秦九韶 课件 20张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 15:43:57 | ||
图片预览







文档简介
(共20张PPT)
海伦和秦九韶
学习目标:
1 、了解“三斜求积”公式,记忆海伦公式,掌握公式推导的方法;
2 、能熟练选择、应用海伦或“三斜求积”公式计算三角形的面积。
3 、培养发现问题、提出问题和分析问题、解决问题的能力,了解我国优秀的传统数学文化,激发数学学习兴趣。
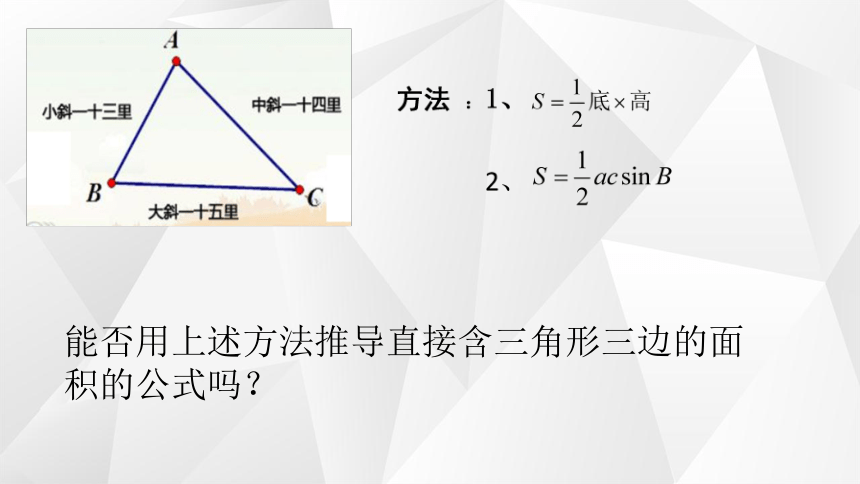
一、问题引领
能否用上述方法推导直接含三角形三边的面积的公式吗?
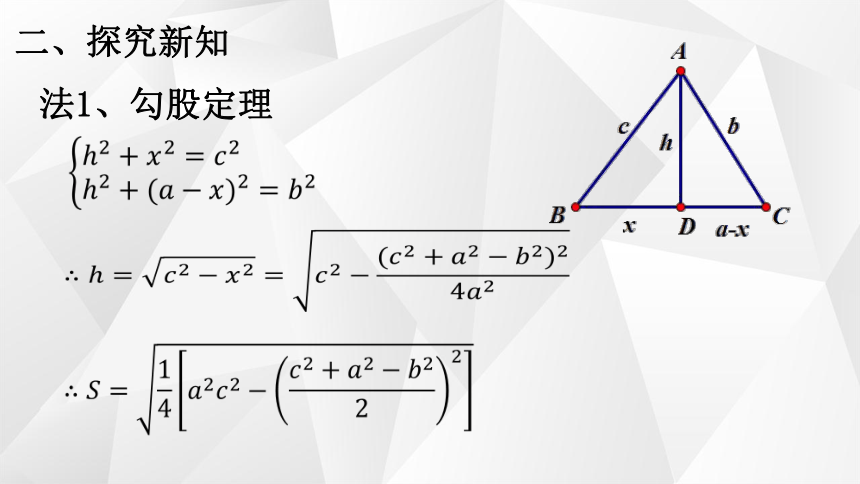
法1、勾股定理
二、探究新知
二、探究新知
秦九韶的三斜求积术
法2、余弦定理
1247年前后,南宋著名的数学家秦九韶在所著的《数书九章》中给出了一个用三边表达三角形面积的公式——三斜求积术,秦九韶把三角形的三条边分别称为小斜、中斜和大斜,“术”即方法.三斜求积术就是:“以小斜幂并大斜幂减中斜幂,余半之,自乘上;以小斜幂乘大斜幂减上,余四约之.为实:一为从隅,开平方得积.”即:
三、文化了解
三、文化了解
三斜求积术是《数书九章》81题中的一个,该书系统总结和发展了高次方程的数值解法和一次同余问题,被誉为“算中宝典”,其中同余理论比西方1801年著名数学家高斯早554年;而任意次方程的数值解,领先英国人霍纳572年,充分说明我国古代已具有很高的数学水平。
虽然海伦公式与秦九韶形式上有所不同,但他们完全等价,你能利用秦九韶公式推导出海伦公式吗?
?
?
?
四、公式证明
?
?
四、公式证明
四、公式证明
四、公式证明
除了上述方法外,还有没有证明海伦公式的方法?
提示1 :三角形内切圆
五、公式应用
例1、
五、公式应用
六、课后练习
七、延伸拓展
任意内接圆的四边形中,设其边长为
Thank you for listening
欢迎批评指正
谢
谢
聆
听
海伦和秦九韶
学习目标:
1 、了解“三斜求积”公式,记忆海伦公式,掌握公式推导的方法;
2 、能熟练选择、应用海伦或“三斜求积”公式计算三角形的面积。
3 、培养发现问题、提出问题和分析问题、解决问题的能力,了解我国优秀的传统数学文化,激发数学学习兴趣。
一、问题引领
能否用上述方法推导直接含三角形三边的面积的公式吗?
法1、勾股定理
二、探究新知
二、探究新知
秦九韶的三斜求积术
法2、余弦定理
1247年前后,南宋著名的数学家秦九韶在所著的《数书九章》中给出了一个用三边表达三角形面积的公式——三斜求积术,秦九韶把三角形的三条边分别称为小斜、中斜和大斜,“术”即方法.三斜求积术就是:“以小斜幂并大斜幂减中斜幂,余半之,自乘上;以小斜幂乘大斜幂减上,余四约之.为实:一为从隅,开平方得积.”即:
三、文化了解
三、文化了解
三斜求积术是《数书九章》81题中的一个,该书系统总结和发展了高次方程的数值解法和一次同余问题,被誉为“算中宝典”,其中同余理论比西方1801年著名数学家高斯早554年;而任意次方程的数值解,领先英国人霍纳572年,充分说明我国古代已具有很高的数学水平。
虽然海伦公式与秦九韶形式上有所不同,但他们完全等价,你能利用秦九韶公式推导出海伦公式吗?
?
?
?
四、公式证明
?
?
四、公式证明
四、公式证明
四、公式证明
除了上述方法外,还有没有证明海伦公式的方法?
提示1 :三角形内切圆
五、公式应用
例1、
五、公式应用
六、课后练习
七、延伸拓展
任意内接圆的四边形中,设其边长为
Thank you for listening
欢迎批评指正
谢
谢
聆
听
