1.2.1 充分条件与必要条件 课件 21张PPT
文档属性
| 名称 | 1.2.1 充分条件与必要条件 课件 21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 288.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
1.2.1 充分条件和必要条件
第一章:常用逻辑用语
复习回顾
1.“若P则q”形式的命题,有的命题是真命题,有的则是假命题
2.两个命题互为逆否命题时,其真假性一致
前面我们讨论了
白鲸性情温顺,喜欢与人接触,受到人类的喜爱。但随着生态环境的变化,它们的生存受到了极大的威胁。白鲸已于2008年列入《世界自然保护联盟濒危物种红色名录》
若白鲸能够生存,则一定有水
真
若有水,则白鲸能够生存
假
问题引入
问题引入
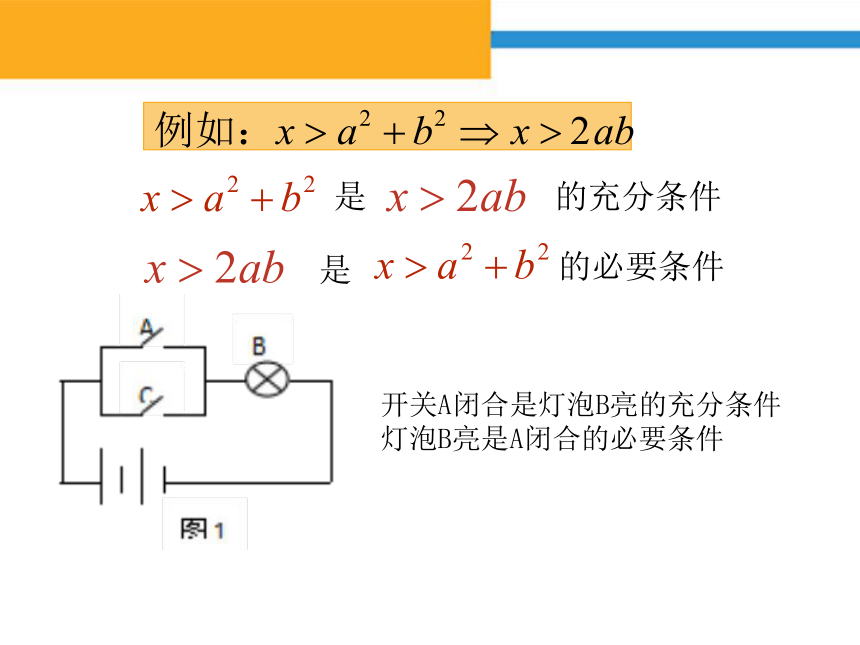
“若开关A闭合,则灯泡B会亮”
是真命题
“若开关A’闭合,则灯泡B'会亮”
是假命题
A’
C’
B’
探究新知
判断下列命题的真假性
假
真
并且说p是q的充分条件,q是p的必要条件
探究新知
是
的必要条件
是
的充分条件
开关A闭合是灯泡B亮的充分条件
灯泡B亮是A闭合的必要条件
概念理解
例1
下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件
练习1,判断下列问题中,p是q的充分条件吗?
概念理解
例2
下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件
即p是q的充分条件
概念理解
q是p的必要条件
p是q的充分条件
逆否命题:我们不是安徽人,则我们不是合肥人
概念深入
————无之必不成立
例如
原命题:我们是合肥人,则我们是安徽人
————有之必成立
“是合肥人”为“是安徽人”的充分条件
“是安徽人”为“是合肥人”的必要条件
《墨经》
充分条件——有之则必然,无之则未必不然
必要条件——无之则必不然,有之则未必然
当“若p,则q”的逆命题成立时,
p是q的什么条件?
小结
原命题“若p则q”为真命题,
逆命题“若q则p”为真命题,
概念深入
知识巩固
练习:用“充分”和“必要”填空
充分
必要
必要
必要
思考
能否从集合的角度理解
充分条件和必要条件?
1
a
b
1
知识联系
集合与充分条件、必要条件的联系
A
B
A、B
例3
已知
知识应用
(2)(3)(4)
知识应用
练习巩固
判断下列各组问题中,p是不是q的充分条件,
以及p是不是q的必要条件
p不是q的充分条件
p是q的必要条件
p是q的充分条件,p不是q的必要条件
p是q的充分条件,p是q的必要条件
p不是q的充分条件,p也不是q的必要条件
课堂小结
充分条件与必要条件的定义
充分条件与必要条件的判断
从集合的角度理解充分条件与必要条件
谢谢
第一章:常用逻辑用语
1.2.1 充分条件和必要条件
第一章:常用逻辑用语
复习回顾
1.“若P则q”形式的命题,有的命题是真命题,有的则是假命题
2.两个命题互为逆否命题时,其真假性一致
前面我们讨论了
白鲸性情温顺,喜欢与人接触,受到人类的喜爱。但随着生态环境的变化,它们的生存受到了极大的威胁。白鲸已于2008年列入《世界自然保护联盟濒危物种红色名录》
若白鲸能够生存,则一定有水
真
若有水,则白鲸能够生存
假
问题引入
问题引入
“若开关A闭合,则灯泡B会亮”
是真命题
“若开关A’闭合,则灯泡B'会亮”
是假命题
A’
C’
B’
探究新知
判断下列命题的真假性
假
真
并且说p是q的充分条件,q是p的必要条件
探究新知
是
的必要条件
是
的充分条件
开关A闭合是灯泡B亮的充分条件
灯泡B亮是A闭合的必要条件
概念理解
例1
下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件
练习1,判断下列问题中,p是q的充分条件吗?
概念理解
例2
下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件
即p是q的充分条件
概念理解
q是p的必要条件
p是q的充分条件
逆否命题:我们不是安徽人,则我们不是合肥人
概念深入
————无之必不成立
例如
原命题:我们是合肥人,则我们是安徽人
————有之必成立
“是合肥人”为“是安徽人”的充分条件
“是安徽人”为“是合肥人”的必要条件
《墨经》
充分条件——有之则必然,无之则未必不然
必要条件——无之则必不然,有之则未必然
当“若p,则q”的逆命题成立时,
p是q的什么条件?
小结
原命题“若p则q”为真命题,
逆命题“若q则p”为真命题,
概念深入
知识巩固
练习:用“充分”和“必要”填空
充分
必要
必要
必要
思考
能否从集合的角度理解
充分条件和必要条件?
1
a
b
1
知识联系
集合与充分条件、必要条件的联系
A
B
A、B
例3
已知
知识应用
(2)(3)(4)
知识应用
练习巩固
判断下列各组问题中,p是不是q的充分条件,
以及p是不是q的必要条件
p不是q的充分条件
p是q的必要条件
p是q的充分条件,p不是q的必要条件
p是q的充分条件,p是q的必要条件
p不是q的充分条件,p也不是q的必要条件
课堂小结
充分条件与必要条件的定义
充分条件与必要条件的判断
从集合的角度理解充分条件与必要条件
谢谢
第一章:常用逻辑用语
