1.3.2 或(or) 课件 19张PPT
文档属性
| 名称 | 1.3.2 或(or) 课件 19张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 679.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
课题名称:数学选修1-1
1.3.2 或(or)
年级:高二
版本: 人教A版
1、教学重点
理解“或”的含义,能根据含义判定由“或”组成的新命题的真假。
2、教学难点
对“或”的含义的理解以及对含有逻辑联结词“或”的问题综合应用。
教学重难点
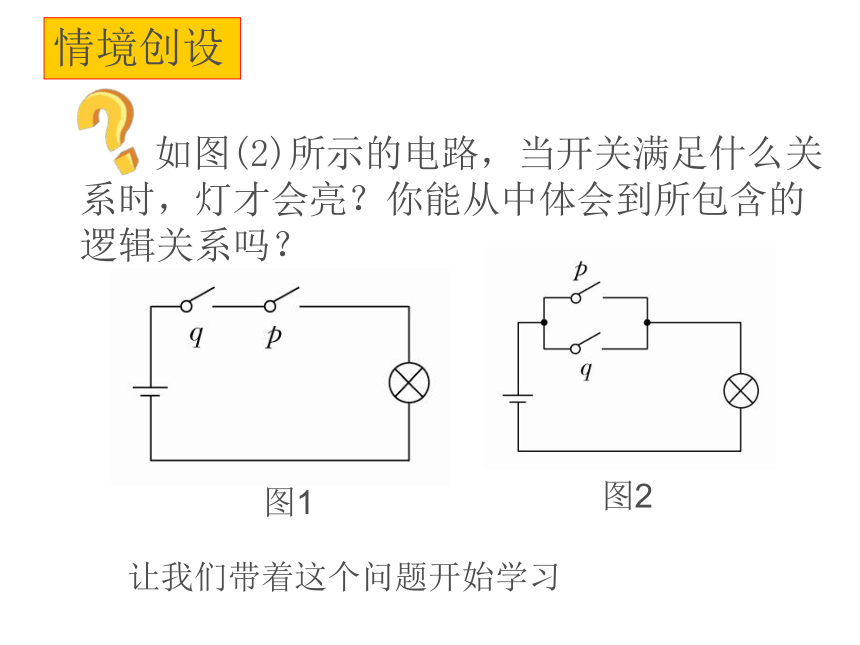
图1
让我们带着这个问题开始学习
图2
情境创设
如图(2)所示的电路,当开关满足什么关系时,灯才会亮?你能从中体会到所包含的逻辑关系吗?
引例:思考下列三个命题间有什么关系?
(1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数或是9的倍数.
可以看出命题(3)是由命题(1)和(2)用联结词“或”联接起来的.
新知探究
定义:一般地,用逻辑联结词 “或”把命题 p 和命题 q 联结起来.就得到一个新命题,记:
读作“ p 或 q ”.
p ∨ q
概念引入
定义:一般地,用逻辑联结词 “或”把命题 p 和命题 q 联结起来.就得到一个新命题,记作
p ∨ q
例1 将下列命题用“或”联结成新命题:
(1)p:平行四边形的对角线互相平分,
q:平行四边形的对角线相等;
(2)p:菱形的对角线互相垂直,
q:菱形的对角线互相平分;
(3)p:相似三角形的面积相等,
q:相似三角形的周长相等。
解析:(1) p ∨q :平行四边形的对角线互相平分或相等。
(2) p ∨q :菱形的对角线互相垂直或平分.
(3) p ∨q :相似三角形的面积相等或周长相等.
例题分析
你能判断它们的真假吗?
命题 p ∨ q 的真假性与命题p 、 q 真假性是否有关?若有关,又有怎样的关系?
真 假
真 真
假 假
例题分析
思考与探究
(1) p:平行四边形的对角线互相平分,
q:平行四边形的对角线相等;
p∨q :平行四边形的对角线互相平分或相等
(2) p:菱形的对角线互相垂直,
q:菱形的对角线互相平分;
p∨q :菱形的对角线互相垂直或平分.
(3) p:相似三角形的面积相等,
q:相似三角形的周长相等。
p∨q :相似三角形的面积相等或周长相等
真
真
假
图2
把开关闭合看作命题为真;把开关断开看作命题为假.
把整个电路的接通与断开分别对应命题p ∨ q真与假。
—
—
本节开始的问题
如图(2)所示的电路,当开关满足什么关系时,灯才会亮?你能从中体会到所包含的逻辑关系吗?
1、将命题p:-1是方程x2+4x+3=0的解,q:-3是方程x2+4x+3=0的解,用联结词“或”联结得到新命题为____________,其为________命题.(填“真”或“假”)
2、命题①sinx≤1或cosx>2是________命题;
②10<10或lg100>2是________命题.(填“真”或“假”)
小试牛刀
【解析】1、由已知得“p∨q”为:-1或-3是方程x2+4x+3=0的解;因为p,q均真,故p∨q为真.
答案:-1或-3是方程x2+4x+3=0的解 真
2、①sinx≤1为真,cosx>2为假,故“p∨q”为真.
②10<10为假,lg100=2>2为假,故“p∨q”为假.
思考与探究
从集合角度理解,本节中的逻辑联结词“或”与并集中的“或”有不同吗?
集合中“并集”的概念.A∪B={x|x∈A或x∈B}中的“或”指“x∈A”“x∈B”中至少有一个是成立的,即可以x∈A且x?B,也可以x?A且x∈B,还可以x∈A且x∈B.
例2 分别指出下列命题的形式,并判断真假:
(1)集合A是A∩B的子集或是A∪B的子集;
(2)周长相等的两个三角形全等或面积相等的两个三角形全等。
(3)2≤2;
巩固提高
解析:(1)该命题是“p ∨ q”形式,其中
p:集合A是A∩B的子集; q:集合A是A∪B的子集;
因为命题q是真命题,所以原命题是真命题.
(2)p:周长相等的两个三角形全等; q:面积相等的两个三角形全等。 用“或”联结后构成的新命题,即p∨q.
因为命题p,q都是假命题,所以命题p∨q是假命题
(3)该命题是“p或q”形式,其中
p:2=2; q:2<2;
因为p是真命题,所以原命题是真命题.
巩固提高
1、指出下列命题的形式及构成.
(1)24是8和6的倍数;(2)2≤3;(3)菱形对角线相互垂直平分;(4)1既不是质数也不是合数;(5)斜三角形的内角是锐角或是钝角
变式训练
【解析】(1)“p∧q”形式,
其中p:24是8的倍数, q:24是6的倍数.
(2)“p∨q”形式,其中p:2<3,q:2=3.
(3)“p∧q”形式,其中p:菱形对角线互相垂直,q:菱形对角线互相平分.
(4)“p∧q”形式,其中p:1不是质数,
q:1不是合数
(5)“p∨q”形式,其中p:斜三角形的内角是锐角.q:斜三角形内角是钝角.
2、(1)如果命题“p或q”是真命题,“p且q”是假命题.那么( )
(A)命题p和命题q都是假命题
(B)命题p和命题q都是真命题
(C)命题p为真命题,q为假命题
(D)命题q和命题p的真假不同
(2)已知p,q是简单命题,则“p或q为真”是“p且q为真”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
变式训练
D
B
例3:命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立;q:函数f(x)=-(5-2a)x是减函数.若p或q为真,p且q为假,求实数a的取值范围.
能力迁移
【解析】设g(x)=x2+2ax+4,因为关于x的不等式x2+2ax+4>0对一切x∈R恒成立,所以函数g(x)的图象开口向上且与x轴没有交点,故Δ=4a2-16<0,所以
-2即命题p:-2函数f(x)=-(5-2a)x是减函数,则有5-2a>1,即a<2.
所以命题q:a<2.
由p或q为真,p且q为假,可知p和q一真一假.
(1)若p真q假,则 此不等式组无解.
(2)若p假q真,则
所以a≤-2.
综上,实数a的取值范围是(-∞,-2].
若将“q:函数f(x)=-(5-2a)x是减函数”改为“q:函数f(x)=-(5-2a)x是增函数”,其他条件不变,求实数a的取值范围.
变式训练
答案:实数a的取值范围是(-2,2)∪
总结提升
思考
通过本节课的学习与探究,你有哪些收获?请分享给大家。
作业
1、习题1.3 B组(1)至(4)
2、各举三组命题p、q,分别写出p∧q, p∨q形式的命题,并判断它们的真假性。
课题名称:数学选修1-1
1.3.2 或(or)
年级:高二
版本: 人教A版
1、教学重点
理解“或”的含义,能根据含义判定由“或”组成的新命题的真假。
2、教学难点
对“或”的含义的理解以及对含有逻辑联结词“或”的问题综合应用。
教学重难点
图1
让我们带着这个问题开始学习
图2
情境创设
如图(2)所示的电路,当开关满足什么关系时,灯才会亮?你能从中体会到所包含的逻辑关系吗?
引例:思考下列三个命题间有什么关系?
(1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数或是9的倍数.
可以看出命题(3)是由命题(1)和(2)用联结词“或”联接起来的.
新知探究
定义:一般地,用逻辑联结词 “或”把命题 p 和命题 q 联结起来.就得到一个新命题,记:
读作“ p 或 q ”.
p ∨ q
概念引入
定义:一般地,用逻辑联结词 “或”把命题 p 和命题 q 联结起来.就得到一个新命题,记作
p ∨ q
例1 将下列命题用“或”联结成新命题:
(1)p:平行四边形的对角线互相平分,
q:平行四边形的对角线相等;
(2)p:菱形的对角线互相垂直,
q:菱形的对角线互相平分;
(3)p:相似三角形的面积相等,
q:相似三角形的周长相等。
解析:(1) p ∨q :平行四边形的对角线互相平分或相等。
(2) p ∨q :菱形的对角线互相垂直或平分.
(3) p ∨q :相似三角形的面积相等或周长相等.
例题分析
你能判断它们的真假吗?
命题 p ∨ q 的真假性与命题p 、 q 真假性是否有关?若有关,又有怎样的关系?
真 假
真 真
假 假
例题分析
思考与探究
(1) p:平行四边形的对角线互相平分,
q:平行四边形的对角线相等;
p∨q :平行四边形的对角线互相平分或相等
(2) p:菱形的对角线互相垂直,
q:菱形的对角线互相平分;
p∨q :菱形的对角线互相垂直或平分.
(3) p:相似三角形的面积相等,
q:相似三角形的周长相等。
p∨q :相似三角形的面积相等或周长相等
真
真
假
图2
把开关闭合看作命题为真;把开关断开看作命题为假.
把整个电路的接通与断开分别对应命题p ∨ q真与假。
—
—
本节开始的问题
如图(2)所示的电路,当开关满足什么关系时,灯才会亮?你能从中体会到所包含的逻辑关系吗?
1、将命题p:-1是方程x2+4x+3=0的解,q:-3是方程x2+4x+3=0的解,用联结词“或”联结得到新命题为____________,其为________命题.(填“真”或“假”)
2、命题①sinx≤1或cosx>2是________命题;
②10<10或lg100>2是________命题.(填“真”或“假”)
小试牛刀
【解析】1、由已知得“p∨q”为:-1或-3是方程x2+4x+3=0的解;因为p,q均真,故p∨q为真.
答案:-1或-3是方程x2+4x+3=0的解 真
2、①sinx≤1为真,cosx>2为假,故“p∨q”为真.
②10<10为假,lg100=2>2为假,故“p∨q”为假.
思考与探究
从集合角度理解,本节中的逻辑联结词“或”与并集中的“或”有不同吗?
集合中“并集”的概念.A∪B={x|x∈A或x∈B}中的“或”指“x∈A”“x∈B”中至少有一个是成立的,即可以x∈A且x?B,也可以x?A且x∈B,还可以x∈A且x∈B.
例2 分别指出下列命题的形式,并判断真假:
(1)集合A是A∩B的子集或是A∪B的子集;
(2)周长相等的两个三角形全等或面积相等的两个三角形全等。
(3)2≤2;
巩固提高
解析:(1)该命题是“p ∨ q”形式,其中
p:集合A是A∩B的子集; q:集合A是A∪B的子集;
因为命题q是真命题,所以原命题是真命题.
(2)p:周长相等的两个三角形全等; q:面积相等的两个三角形全等。 用“或”联结后构成的新命题,即p∨q.
因为命题p,q都是假命题,所以命题p∨q是假命题
(3)该命题是“p或q”形式,其中
p:2=2; q:2<2;
因为p是真命题,所以原命题是真命题.
巩固提高
1、指出下列命题的形式及构成.
(1)24是8和6的倍数;(2)2≤3;(3)菱形对角线相互垂直平分;(4)1既不是质数也不是合数;(5)斜三角形的内角是锐角或是钝角
变式训练
【解析】(1)“p∧q”形式,
其中p:24是8的倍数, q:24是6的倍数.
(2)“p∨q”形式,其中p:2<3,q:2=3.
(3)“p∧q”形式,其中p:菱形对角线互相垂直,q:菱形对角线互相平分.
(4)“p∧q”形式,其中p:1不是质数,
q:1不是合数
(5)“p∨q”形式,其中p:斜三角形的内角是锐角.q:斜三角形内角是钝角.
2、(1)如果命题“p或q”是真命题,“p且q”是假命题.那么( )
(A)命题p和命题q都是假命题
(B)命题p和命题q都是真命题
(C)命题p为真命题,q为假命题
(D)命题q和命题p的真假不同
(2)已知p,q是简单命题,则“p或q为真”是“p且q为真”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
变式训练
D
B
例3:命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立;q:函数f(x)=-(5-2a)x是减函数.若p或q为真,p且q为假,求实数a的取值范围.
能力迁移
【解析】设g(x)=x2+2ax+4,因为关于x的不等式x2+2ax+4>0对一切x∈R恒成立,所以函数g(x)的图象开口向上且与x轴没有交点,故Δ=4a2-16<0,所以
-2
所以命题q:a<2.
由p或q为真,p且q为假,可知p和q一真一假.
(1)若p真q假,则 此不等式组无解.
(2)若p假q真,则
所以a≤-2.
综上,实数a的取值范围是(-∞,-2].
若将“q:函数f(x)=-(5-2a)x是减函数”改为“q:函数f(x)=-(5-2a)x是增函数”,其他条件不变,求实数a的取值范围.
变式训练
答案:实数a的取值范围是(-2,2)∪
总结提升
思考
通过本节课的学习与探究,你有哪些收获?请分享给大家。
作业
1、习题1.3 B组(1)至(4)
2、各举三组命题p、q,分别写出p∧q, p∨q形式的命题,并判断它们的真假性。
