第一章 常用逻辑用语 复习小结 课件 17张PPT
文档属性
| 名称 | 第一章 常用逻辑用语 复习小结 课件 17张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 602.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
常用逻辑用语复习小结
选修1-1/第一章/常用逻辑用语/复习课
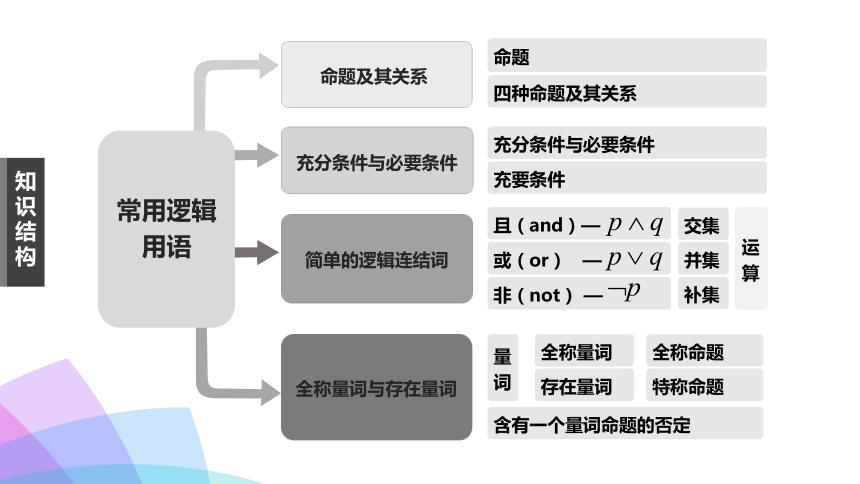
命题及其关系
充分条件与必要条件
简单的逻辑连结词
全称量词与存在量词
常用逻辑用语
四种命题及其关系
命题
充分条件与必要条件
充要条件
量词
全称量词
存在量词
全称命题
特称命题
含有一个量词命题的否定
或(or) —
且(and)—
非(not) —
交集
并集
补集
运算
知识结构
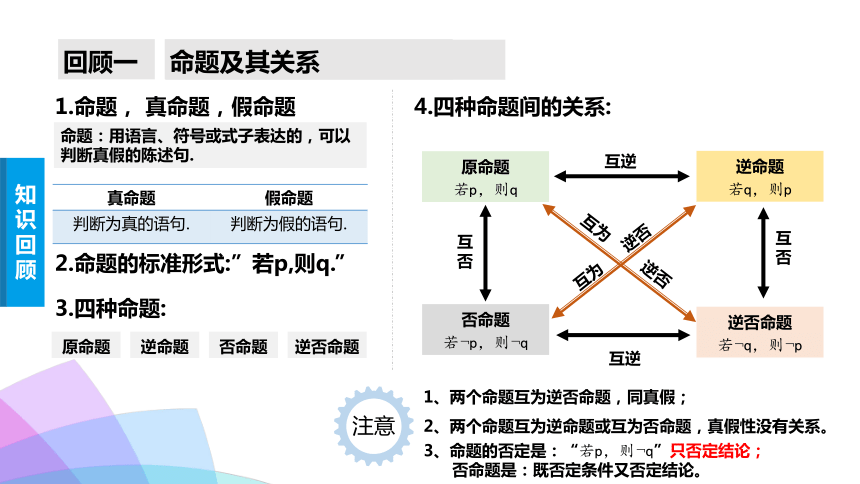
1.命题, 真命题,假命题
2.命题的标准形式:”若p,则q.”
3.四种命题:
命题及其关系
回顾一
命题及其关系
命题:用语言、符号或式子表达的,可以判断真假的陈述句.
原命题
逆命题
否命题
逆否命题
真命题 假命题
判断为真的语句. 判断为假的语句.
1、两个命题互为逆否命题,同真假;
2、两个命题互为逆命题或互为否命题,真假性没有关系。
3、命题的否定是:“若p,则﹁q”只否定结论;
否命题是:既否定条件又否定结论。
注意
知识回顾
4.四种命题间的关系:
原命题
若p,则q
互逆
互否
互否
互逆
否命题
若﹁p,则﹁q
逆命题
若q,则p
逆否命题
若﹁q,则﹁p
互为 逆否
互为 逆否
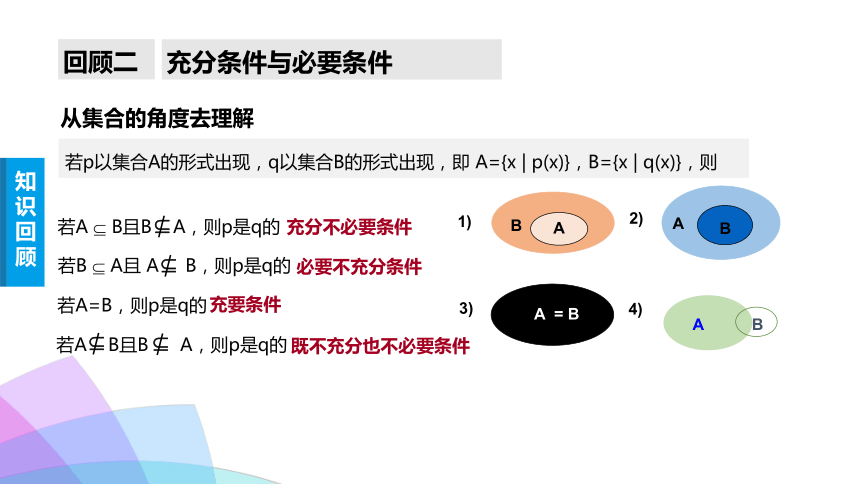
充分条件与必要条件
回顾二
从概念的角度去理解
若p ? q,则称p是q的充分条件,q是p的必要条件.
p是q的充分不必要条件
p是q的必要不充分条件
p是q的充要条件
p是q的既不充分不必要条件
知识回顾
回顾二
充分条件与必要条件
充要条件
充分不必要条件
必要不充分条件
既不充分也不必要条件
从集合的角度去理解
若p以集合A的形式出现,q以集合B的形式出现,即 A={x | p(x)},B={x | q(x)},则
若A=B,则p是q的
?
若A ? B且B A,则p是q的
?
若B ? A且 A B,则p是q的
?
?
若A B且B A,则p是q的
B
A
1)
A
B
2)
A
B
4)
A = B
3)
知识回顾
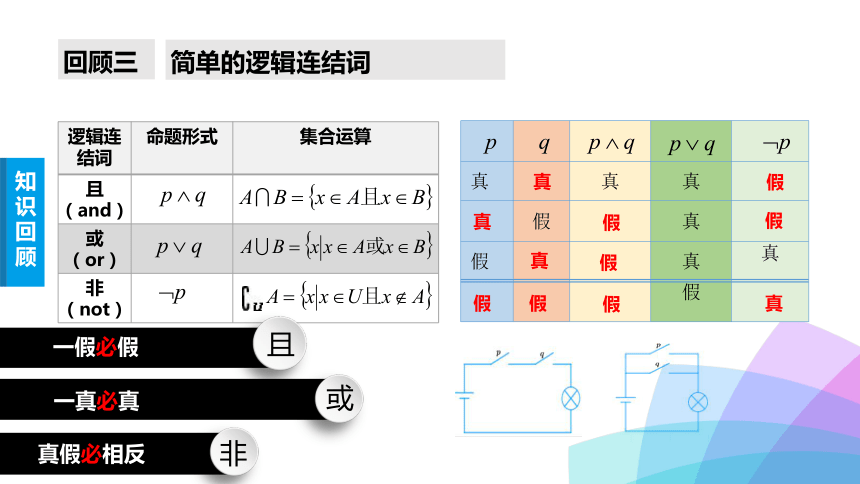
简单的逻辑连结词
回顾三
逻辑连结词 命题形式 集合运算
且(and)
或
(or)
非(not)
真 ? 真 真 ?
? 假 ? 真 ?
假 ? ? 真 真
? ? ? 假 ?
知识回顾
真
真
假
假
假
假
真
真
假
假
假
一假必假
一真必真
真假必相反
且
或
非
回顾四
全称量词与存在量词
全称量词
——“所有的”、“任意一个”等,用“ ”表示。
——“存在一个”、“至少有一个”等,用“ ”表示。
存在量词
命题类型 全称命题 特称命题
形式
否定
Tips
无论是全称命题还是特称命题,其真假不容易正面判断时,都可先判断其否定的真假。
否定
方法
知识回顾
命题及其关系
回顾四
全称量词与存在量词
特别注意对一些词语的否定
词语 否定 词语 否定
等于 不等于 任意的 某个
大于 不大于 所有的 某些
小于 不小于 且 或
是 不是 都是 不都是
至多有一个 至少有两个 至多有n个 至少有(n+1)个
至少有一个 一个都没有 至少有n个 至多有(n-1)个
知识回顾
例题 1
四种命题及其关系
基础练习
两个命题互为逆否命题,同真假;
1
四个命题中,正确的个数一定为偶数;
2
例题 2
充分条件与必要条件的判断
基础练习
C. 充要条件
D. 既不充分也不必要条件
在数列 中,“ ”是“ 是公比为 的等比数列”的( )
例题:
A. 充分不必要条件
B. 必要不充分条件
B
例题 2
充分条件与必要条件的判断
基础练习
方法归纳
2
从集合的角度判断:利用集合中包含思想判定。抓住“以小推大”的技巧,即小范围推得大范围,即可解决充分必要性的问题。
例题:
1
利用定义判断:直接判断“若p,则q”“若q,则p”的真假。在判断时,确定条件是什么,结论是什么。
命题及其关系
例题 3
根据充分、必要条件求参数的取值范围
基础练习
例题:
是否存在实数 , 使得 是 的充分条件?
记集合即 A={x | p(x)},B={x | q(x)};
根据相应的充分必要条件确定集合A与B的包含关系;
根据集合A与B的包含关系建立关于参数的不等式(组);
解不等式(组)求出参数的取值范围。
0
1
2
3
-1
x
解:
由 得: .
是 的充分条件。
由 得: .
应有 .
如图所示。
即: .
所以存在实数m,使 是 的充分条件。
例题 4
含逻辑连结词的命题的真假的判断
基础练习
方法归纳
确定命题的构成形式;
判断命题p,q的真假;
根据真值表确定命题的真假。
C
例题5
含有一个量词的命题的否定
基础练习
命题“ ”的否定是__________________________。
______________时,此命题为真命题。
例题:
当
答案:
2
无论是全称命题还是特称命题,其真假不容易正面判断时,都可先判断其否定的真假。
归纳
感悟
1
1. 明确这个命题是全称命题还是特称命题;
2. 找到量词及相应结论;
3. 把命题中的全称量词改成存在量词,存在量词改成全称量词,同时否定结论,即得其否定。
1
2
3
求出当命题p,q为真命题时所含参数的取值范围;
判断命题p,q的真假性;
根据命题的真假情况,利用集合的交集和补集的运算,求解参数的取值范围。
练习 6
利用含逻辑连结词的命题的真假求参数的取值范围
方法归纳
设
和
,
且“ ”为真,
且“ ”为假,求实数 的取值范围。
例题:
基础练习
答案:
1
2
命题及其关系
充分条件与必要条件
3
简单的逻辑连结词
4
全称量词与存在量词
本章小结
等价转化思想
分类讨论思想
数形结合思想
作业:
1、习题1.1第2.3题
2、能力培养与测试1.1
常用逻辑用语复习小结
选修1-1/第一章/常用逻辑用语/复习课
命题及其关系
充分条件与必要条件
简单的逻辑连结词
全称量词与存在量词
常用逻辑用语
四种命题及其关系
命题
充分条件与必要条件
充要条件
量词
全称量词
存在量词
全称命题
特称命题
含有一个量词命题的否定
或(or) —
且(and)—
非(not) —
交集
并集
补集
运算
知识结构
1.命题, 真命题,假命题
2.命题的标准形式:”若p,则q.”
3.四种命题:
命题及其关系
回顾一
命题及其关系
命题:用语言、符号或式子表达的,可以判断真假的陈述句.
原命题
逆命题
否命题
逆否命题
真命题 假命题
判断为真的语句. 判断为假的语句.
1、两个命题互为逆否命题,同真假;
2、两个命题互为逆命题或互为否命题,真假性没有关系。
3、命题的否定是:“若p,则﹁q”只否定结论;
否命题是:既否定条件又否定结论。
注意
知识回顾
4.四种命题间的关系:
原命题
若p,则q
互逆
互否
互否
互逆
否命题
若﹁p,则﹁q
逆命题
若q,则p
逆否命题
若﹁q,则﹁p
互为 逆否
互为 逆否
充分条件与必要条件
回顾二
从概念的角度去理解
若p ? q,则称p是q的充分条件,q是p的必要条件.
p是q的充分不必要条件
p是q的必要不充分条件
p是q的充要条件
p是q的既不充分不必要条件
知识回顾
回顾二
充分条件与必要条件
充要条件
充分不必要条件
必要不充分条件
既不充分也不必要条件
从集合的角度去理解
若p以集合A的形式出现,q以集合B的形式出现,即 A={x | p(x)},B={x | q(x)},则
若A=B,则p是q的
?
若A ? B且B A,则p是q的
?
若B ? A且 A B,则p是q的
?
?
若A B且B A,则p是q的
B
A
1)
A
B
2)
A
B
4)
A = B
3)
知识回顾
简单的逻辑连结词
回顾三
逻辑连结词 命题形式 集合运算
且(and)
或
(or)
非(not)
真 ? 真 真 ?
? 假 ? 真 ?
假 ? ? 真 真
? ? ? 假 ?
知识回顾
真
真
假
假
假
假
真
真
假
假
假
一假必假
一真必真
真假必相反
且
或
非
回顾四
全称量词与存在量词
全称量词
——“所有的”、“任意一个”等,用“ ”表示。
——“存在一个”、“至少有一个”等,用“ ”表示。
存在量词
命题类型 全称命题 特称命题
形式
否定
Tips
无论是全称命题还是特称命题,其真假不容易正面判断时,都可先判断其否定的真假。
否定
方法
知识回顾
命题及其关系
回顾四
全称量词与存在量词
特别注意对一些词语的否定
词语 否定 词语 否定
等于 不等于 任意的 某个
大于 不大于 所有的 某些
小于 不小于 且 或
是 不是 都是 不都是
至多有一个 至少有两个 至多有n个 至少有(n+1)个
至少有一个 一个都没有 至少有n个 至多有(n-1)个
知识回顾
例题 1
四种命题及其关系
基础练习
两个命题互为逆否命题,同真假;
1
四个命题中,正确的个数一定为偶数;
2
例题 2
充分条件与必要条件的判断
基础练习
C. 充要条件
D. 既不充分也不必要条件
在数列 中,“ ”是“ 是公比为 的等比数列”的( )
例题:
A. 充分不必要条件
B. 必要不充分条件
B
例题 2
充分条件与必要条件的判断
基础练习
方法归纳
2
从集合的角度判断:利用集合中包含思想判定。抓住“以小推大”的技巧,即小范围推得大范围,即可解决充分必要性的问题。
例题:
1
利用定义判断:直接判断“若p,则q”“若q,则p”的真假。在判断时,确定条件是什么,结论是什么。
命题及其关系
例题 3
根据充分、必要条件求参数的取值范围
基础练习
例题:
是否存在实数 , 使得 是 的充分条件?
记集合即 A={x | p(x)},B={x | q(x)};
根据相应的充分必要条件确定集合A与B的包含关系;
根据集合A与B的包含关系建立关于参数的不等式(组);
解不等式(组)求出参数的取值范围。
0
1
2
3
-1
x
解:
由 得: .
是 的充分条件。
由 得: .
应有 .
如图所示。
即: .
所以存在实数m,使 是 的充分条件。
例题 4
含逻辑连结词的命题的真假的判断
基础练习
方法归纳
确定命题的构成形式;
判断命题p,q的真假;
根据真值表确定命题的真假。
C
例题5
含有一个量词的命题的否定
基础练习
命题“ ”的否定是__________________________。
______________时,此命题为真命题。
例题:
当
答案:
2
无论是全称命题还是特称命题,其真假不容易正面判断时,都可先判断其否定的真假。
归纳
感悟
1
1. 明确这个命题是全称命题还是特称命题;
2. 找到量词及相应结论;
3. 把命题中的全称量词改成存在量词,存在量词改成全称量词,同时否定结论,即得其否定。
1
2
3
求出当命题p,q为真命题时所含参数的取值范围;
判断命题p,q的真假性;
根据命题的真假情况,利用集合的交集和补集的运算,求解参数的取值范围。
练习 6
利用含逻辑连结词的命题的真假求参数的取值范围
方法归纳
设
和
,
且“ ”为真,
且“ ”为假,求实数 的取值范围。
例题:
基础练习
答案:
1
2
命题及其关系
充分条件与必要条件
3
简单的逻辑连结词
4
全称量词与存在量词
本章小结
等价转化思想
分类讨论思想
数形结合思想
作业:
1、习题1.1第2.3题
2、能力培养与测试1.1
