18.2.3 正方形性质同步练习1(附答案)
文档属性
| 名称 | 18.2.3 正方形性质同步练习1(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 225.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 09:33:56 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十八章 平行四边形
18.2.3正方形性质 同步练习
一、单选题(共5题;共10分)
1.如图,在正方形ABCD中,点E是BC延长线上的一点,且AC=EC,连接AE,交CD于点F,若AB=1,则线段DF的长是(?? )
A.?????????????????????????????????????B.?????????????????????????????????????C.?2﹣ ????????????????????????????????????D.? ﹣1
2.正方形具有而菱形不一定具有的性质是(?? ).
A.?四条边都相等???????????B.?对角线互相垂直且平分??????????
?C.?对角线相等???????? ???D.?对角线平分一组对角
3.如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为(????? )
A.????????????????????????????????????????B.?3???????????????????????????????????????C.????????????????????????????????????????D.?5
4.正方形具有而菱形不一定具有的特征是(?? )
A.?对角线互相垂直平分??????????????B.?内角和为360°???????????
??C.?对角线相等?????????? ????D.?对角线平分内角
5.下列命题正确的是(?? )
A.?平行四边形的对角线互相垂直平分??????????????????????B.?矩形的对角线互相垂直平分
C.?菱形的对角线互相平分且相等?????????????????????????????D.?正方形的对角线互相垂直平分
二、填空题(共4题;共4分)
6.如果正方形的对角线长为 ,那么这个正方形的面积为________.
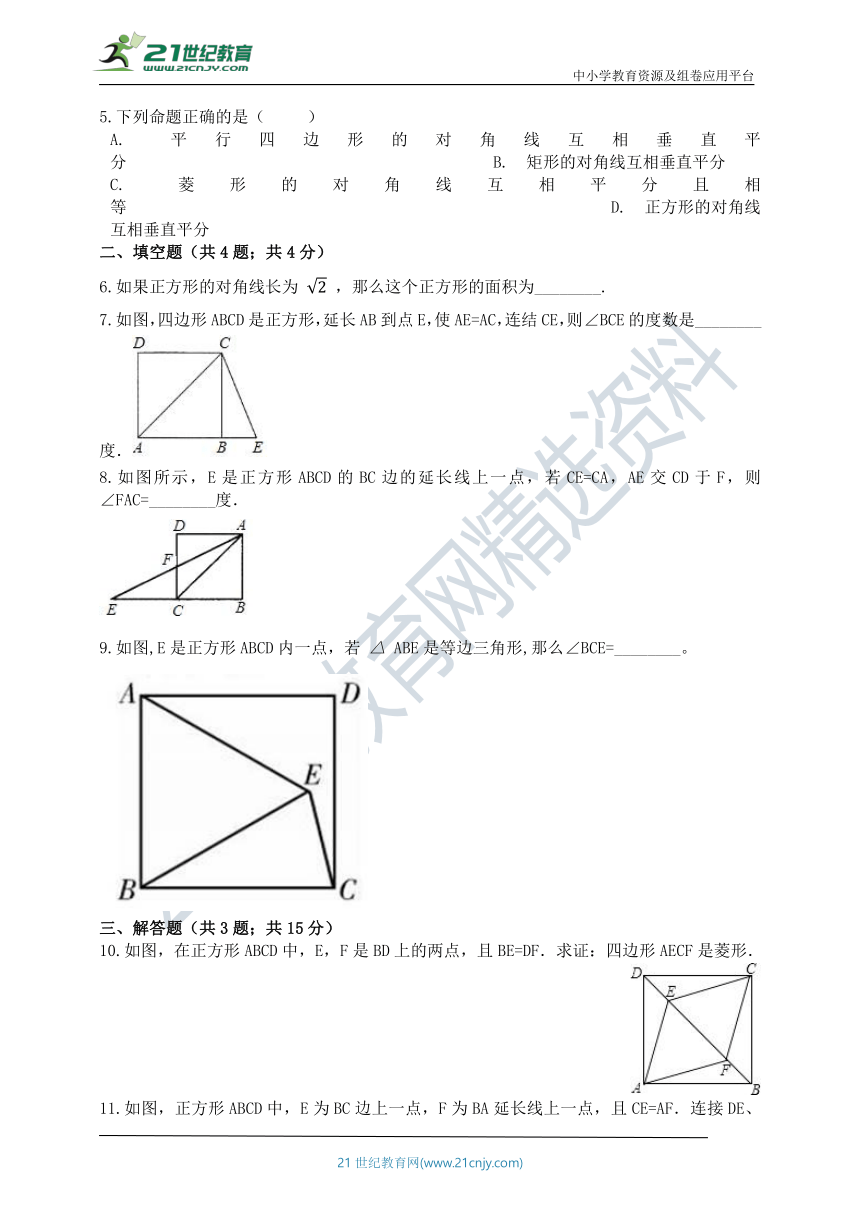
7.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,连结CE,则∠BCE的度数是________度.
8.如图所示,E是正方形ABCD的BC边的延长线上一点,若CE=CA,AE交CD于F,则∠FAC=________度.
9.如图,E是正方形ABCD内一点,若 ABE是等边三角形,那么∠BCE=________。
三、解答题(共3题;共15分)
10.如图,在正方形ABCD中,E,F是BD上的两点,且BE=DF.求证:四边形AECF是菱形.
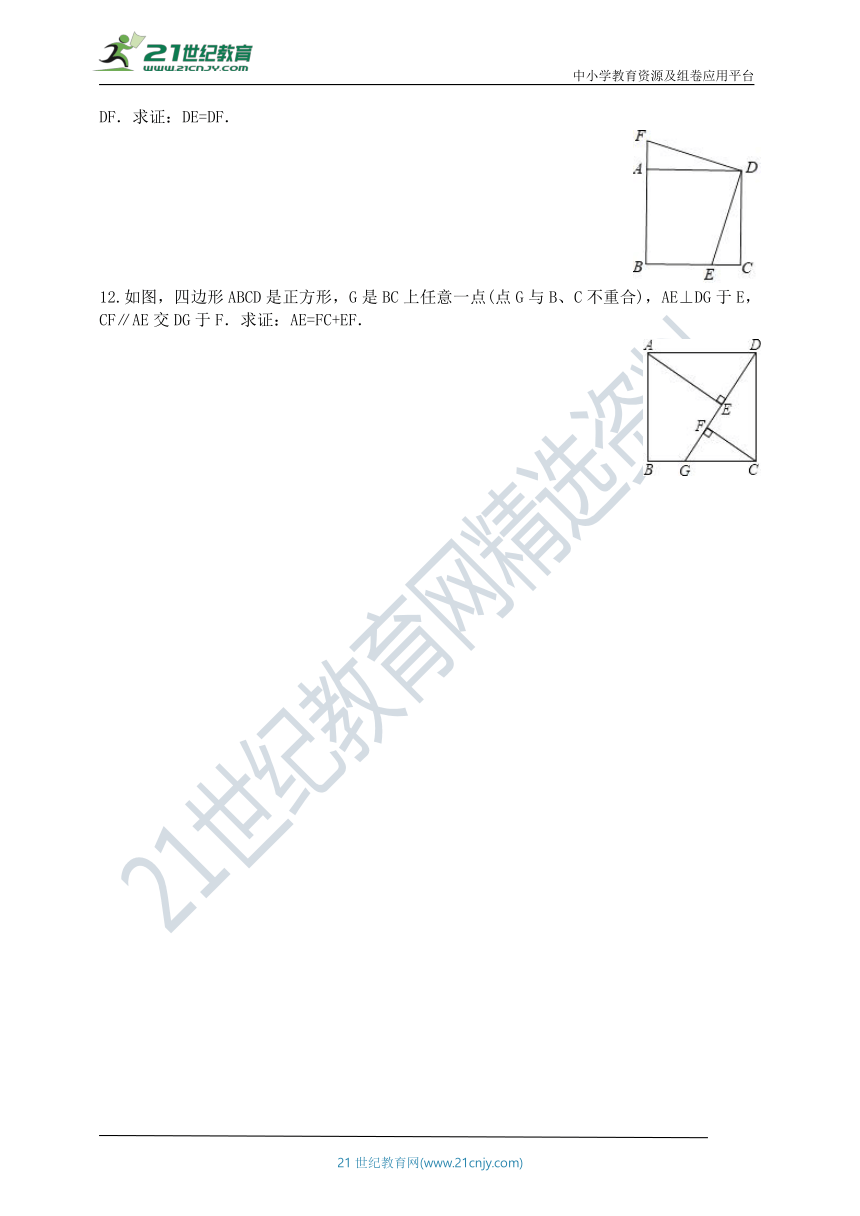
11.如图,正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF.连接DE、DF.求证:DE=DF.
12.如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF∥AE交DG于F.求证:AE=FC+EF.
?
参考答案
一、单选题
1.【答案】 D
【解析】【解答】∵四边形ABCD是正方形,AB=1,
∴AB=CD=AD=1,AC=CE= ,AD∥CE,
∴△ADF∽△ECF,
∴ ,
∴
∴DF= ﹣1
故答案为:D.
【分析】由正方形的性质可得AB=CD=AD=1,AC=CE= ,AD∥CE,通过证明△ADF∽△ECF,可得 ,即可求解.
2.【答案】 C
【解析】【解答】解:A、正方形和菱形的四条边都相等,故A不合题意;
B、正方形和菱形的对角线都互相垂直且平分,故B不合题意;
C、正方形的对角线相等,菱形的对角线不相等,故C合题意;
D、正方形和菱形的对角线都平分一组对角,故D不合题意;
故选:C.
【分析】正方形的四条边相等,对角线互相垂直、平分、相等,且对角线平分一组对角;菱形的四条边相等,对角线互相垂直平分且平分一组对角,据此逐一判断即可.
3.【答案】 B
【解析】【解答】解:∵四边形ABCD是正方形,
∴∠B=90°,
∴BC2=EC2﹣EB2=22﹣12=3,
∴正方形ABCD的面积=BC2=3,
故答案为:B。
【分析】根据正方形的四个角都是直角得出∠B=90°,从而利用勾股定理得出BC2 , 最后根据正方形ABCD的面积等于BC2即可得出答案。
4.【答案】 C
【解析】【解答】A选项中对角线互相垂直平分的有菱形和正方形;
B选项中所有的四边形的内角和为360°;
C选项中对角线相等的有矩形和正方形;
D选项中对角线平分内角的有菱形。
故答案为:C
【分析】正方形具有平行四边形、菱形和矩形的一切性质;菱形的性质是对边平行且相等,对角相等,对角线互相垂直平分且一条对角线平分一组对角;矩形的性质是对边平行且相等,对角相等,对角线相等且互相平分。
5.【答案】D
【解析】【解答】A、平行四边形的对角线互相平分,故A不符合题意;
B、矩形的对角线相等且互相平分,故B不符合题意;
C、菱形的对角线互相垂直平分,每一条对角线平分一组对角,故C不符合题意;
D、正方形的对角线互相垂直平分,故D符合题意,
故答案为:D.
【分析】此题实质就是区分几种特殊的四边形的对角线的性质:根据平行四边形对角线互相平分;矩形的对角线相等且互相平分;菱形的对角线互相垂直平分,每一条对角线平分一组对角;正方形的对角线相等且互相垂直平分;即可一一判断得出答案。
二、填空题
6.【答案】 1
【解析】【解答】正方形的面积= .
故答案为:1.
【分析】根据正方形的面积等于对角线乘积的一半求解即可.
7.【答案】22.5
【解析】【解答】∵四边形ABCD是正方形,∴∠CAB=∠BCA=45°;△ACE中,AC=AE,则:
∠ACE=∠AEC= (180°﹣∠CAE)=67.5°;
∴∠BCE=∠ACE﹣∠ACB=22.5°.
【分析】根据正方形的性质得出∠CAB=∠BCA=45°;根据等腰三角形的性质得出∠ACE=∠AEC=?(180°﹣∠CAE)=67.5°;再根据角的和差即可算出答案。
8.【答案】22.5
【解析】【解答】解:∵AC为正方形ABCD的对角线
∴∠ACB=45°
∵CE=CA
∴∠CEA=∠CAE
∵∠ACB是∠CEA和∠CAE的外角
∴∠FAC=22.5°
故答案为:22.5.
【分析】先根据正方形的性质及等边对等角的性质可得到,∠CEA=∠CAE,再根据外角的性质即可求得∠FAC的度数.
9.【答案】 75
【解析】【解答】解:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
?∵△ABE是等边三角形 ,
∴∠ABE=60°,BE=AB,
∴∠EBC=∠ABC-∠ABE=30°,BE=BC,
∴∠BCE=(180°-30°)75°.
故答案为:75.
【分析】利用正方形及等边三角形的性质可得∠EBC=∠ABC-∠ABE=30°,BE=BC,根据等腰三角形及三角形内角和定理即可求出结论.
三、解答题
10.【答案】明:∵四边形ABCD是正方形, ∴OD=OB,OA=OC,BD⊥AC,
∵BE=DF,
∴DE=BF,
∴OE=OF,
∴四边形AECF是平行四边形,
∴四边形AECF为菱形.
【解析】【分析】由对角线互相垂直平分的四边形是菱形,AO=CO,EO=FO,AC⊥EF即可证得.
11.【答案】证明:正方形ABCD中,AD=CD,∠BAD=∠C=90°, 所以,∠DAF=90°,
所以,∠DAF=∠C,
在△ADF和△CDE中, ,
∴△ADF≌△CDE(SAS),
∴DE=DF.
【解析】【分析】根据正方形的性质可得AD=CD,∠BAD=∠C=90°,然后求出∠DAF=∠C,再利用“边角边”证明△ADF和△CDE全等,根据全等三角形对应边相等证明即可.
12.【答案】解:∵四边形ABCD是正方形,∴AD=DC,∠ADC=90°,
又∵AE⊥DG,CF∥AE,∴∠AED=∠DFC=90°,
∴∠EAD+∠ADE=∠FDC+∠ADE=90°,∴∠EAD=∠FDC,
∴△AED≌△DFC(AAS),∴AE=DF,ED=FC,
∵DF=DE+EF,∴AE=FC+EF
【解析】【分析】利用正方形的特性可知AD=DC,∠ADC=90°,再结合题中所给的有关角的等量关系可证明△AED≌△DFC.得到AE=DF,ED=FC,容易发现DF=DE+EF,进行边的等量代换即可得证.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十八章 平行四边形
18.2.3正方形性质 同步练习
一、单选题(共5题;共10分)
1.如图,在正方形ABCD中,点E是BC延长线上的一点,且AC=EC,连接AE,交CD于点F,若AB=1,则线段DF的长是(?? )
A.?????????????????????????????????????B.?????????????????????????????????????C.?2﹣ ????????????????????????????????????D.? ﹣1
2.正方形具有而菱形不一定具有的性质是(?? ).
A.?四条边都相等???????????B.?对角线互相垂直且平分??????????
?C.?对角线相等???????? ???D.?对角线平分一组对角
3.如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为(????? )
A.????????????????????????????????????????B.?3???????????????????????????????????????C.????????????????????????????????????????D.?5
4.正方形具有而菱形不一定具有的特征是(?? )
A.?对角线互相垂直平分??????????????B.?内角和为360°???????????
??C.?对角线相等?????????? ????D.?对角线平分内角
5.下列命题正确的是(?? )
A.?平行四边形的对角线互相垂直平分??????????????????????B.?矩形的对角线互相垂直平分
C.?菱形的对角线互相平分且相等?????????????????????????????D.?正方形的对角线互相垂直平分
二、填空题(共4题;共4分)
6.如果正方形的对角线长为 ,那么这个正方形的面积为________.
7.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,连结CE,则∠BCE的度数是________度.
8.如图所示,E是正方形ABCD的BC边的延长线上一点,若CE=CA,AE交CD于F,则∠FAC=________度.
9.如图,E是正方形ABCD内一点,若 ABE是等边三角形,那么∠BCE=________。
三、解答题(共3题;共15分)
10.如图,在正方形ABCD中,E,F是BD上的两点,且BE=DF.求证:四边形AECF是菱形.
11.如图,正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF.连接DE、DF.求证:DE=DF.
12.如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF∥AE交DG于F.求证:AE=FC+EF.
?
参考答案
一、单选题
1.【答案】 D
【解析】【解答】∵四边形ABCD是正方形,AB=1,
∴AB=CD=AD=1,AC=CE= ,AD∥CE,
∴△ADF∽△ECF,
∴ ,
∴
∴DF= ﹣1
故答案为:D.
【分析】由正方形的性质可得AB=CD=AD=1,AC=CE= ,AD∥CE,通过证明△ADF∽△ECF,可得 ,即可求解.
2.【答案】 C
【解析】【解答】解:A、正方形和菱形的四条边都相等,故A不合题意;
B、正方形和菱形的对角线都互相垂直且平分,故B不合题意;
C、正方形的对角线相等,菱形的对角线不相等,故C合题意;
D、正方形和菱形的对角线都平分一组对角,故D不合题意;
故选:C.
【分析】正方形的四条边相等,对角线互相垂直、平分、相等,且对角线平分一组对角;菱形的四条边相等,对角线互相垂直平分且平分一组对角,据此逐一判断即可.
3.【答案】 B
【解析】【解答】解:∵四边形ABCD是正方形,
∴∠B=90°,
∴BC2=EC2﹣EB2=22﹣12=3,
∴正方形ABCD的面积=BC2=3,
故答案为:B。
【分析】根据正方形的四个角都是直角得出∠B=90°,从而利用勾股定理得出BC2 , 最后根据正方形ABCD的面积等于BC2即可得出答案。
4.【答案】 C
【解析】【解答】A选项中对角线互相垂直平分的有菱形和正方形;
B选项中所有的四边形的内角和为360°;
C选项中对角线相等的有矩形和正方形;
D选项中对角线平分内角的有菱形。
故答案为:C
【分析】正方形具有平行四边形、菱形和矩形的一切性质;菱形的性质是对边平行且相等,对角相等,对角线互相垂直平分且一条对角线平分一组对角;矩形的性质是对边平行且相等,对角相等,对角线相等且互相平分。
5.【答案】D
【解析】【解答】A、平行四边形的对角线互相平分,故A不符合题意;
B、矩形的对角线相等且互相平分,故B不符合题意;
C、菱形的对角线互相垂直平分,每一条对角线平分一组对角,故C不符合题意;
D、正方形的对角线互相垂直平分,故D符合题意,
故答案为:D.
【分析】此题实质就是区分几种特殊的四边形的对角线的性质:根据平行四边形对角线互相平分;矩形的对角线相等且互相平分;菱形的对角线互相垂直平分,每一条对角线平分一组对角;正方形的对角线相等且互相垂直平分;即可一一判断得出答案。
二、填空题
6.【答案】 1
【解析】【解答】正方形的面积= .
故答案为:1.
【分析】根据正方形的面积等于对角线乘积的一半求解即可.
7.【答案】22.5
【解析】【解答】∵四边形ABCD是正方形,∴∠CAB=∠BCA=45°;△ACE中,AC=AE,则:
∠ACE=∠AEC= (180°﹣∠CAE)=67.5°;
∴∠BCE=∠ACE﹣∠ACB=22.5°.
【分析】根据正方形的性质得出∠CAB=∠BCA=45°;根据等腰三角形的性质得出∠ACE=∠AEC=?(180°﹣∠CAE)=67.5°;再根据角的和差即可算出答案。
8.【答案】22.5
【解析】【解答】解:∵AC为正方形ABCD的对角线
∴∠ACB=45°
∵CE=CA
∴∠CEA=∠CAE
∵∠ACB是∠CEA和∠CAE的外角
∴∠FAC=22.5°
故答案为:22.5.
【分析】先根据正方形的性质及等边对等角的性质可得到,∠CEA=∠CAE,再根据外角的性质即可求得∠FAC的度数.
9.【答案】 75
【解析】【解答】解:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
?∵△ABE是等边三角形 ,
∴∠ABE=60°,BE=AB,
∴∠EBC=∠ABC-∠ABE=30°,BE=BC,
∴∠BCE=(180°-30°)75°.
故答案为:75.
【分析】利用正方形及等边三角形的性质可得∠EBC=∠ABC-∠ABE=30°,BE=BC,根据等腰三角形及三角形内角和定理即可求出结论.
三、解答题
10.【答案】明:∵四边形ABCD是正方形, ∴OD=OB,OA=OC,BD⊥AC,
∵BE=DF,
∴DE=BF,
∴OE=OF,
∴四边形AECF是平行四边形,
∴四边形AECF为菱形.
【解析】【分析】由对角线互相垂直平分的四边形是菱形,AO=CO,EO=FO,AC⊥EF即可证得.
11.【答案】证明:正方形ABCD中,AD=CD,∠BAD=∠C=90°, 所以,∠DAF=90°,
所以,∠DAF=∠C,
在△ADF和△CDE中, ,
∴△ADF≌△CDE(SAS),
∴DE=DF.
【解析】【分析】根据正方形的性质可得AD=CD,∠BAD=∠C=90°,然后求出∠DAF=∠C,再利用“边角边”证明△ADF和△CDE全等,根据全等三角形对应边相等证明即可.
12.【答案】解:∵四边形ABCD是正方形,∴AD=DC,∠ADC=90°,
又∵AE⊥DG,CF∥AE,∴∠AED=∠DFC=90°,
∴∠EAD+∠ADE=∠FDC+∠ADE=90°,∴∠EAD=∠FDC,
∴△AED≌△DFC(AAS),∴AE=DF,ED=FC,
∵DF=DE+EF,∴AE=FC+EF
【解析】【分析】利用正方形的特性可知AD=DC,∠ADC=90°,再结合题中所给的有关角的等量关系可证明△AED≌△DFC.得到AE=DF,ED=FC,容易发现DF=DE+EF,进行边的等量代换即可得证.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
