人教版九年级数学下册27.2.3相似三角形的应用举例课件(第2课时 共20张PPT)
文档属性
| 名称 | 人教版九年级数学下册27.2.3相似三角形的应用举例课件(第2课时 共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 875.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 21:59:45 | ||
图片预览




文档简介
课件20张PPT。27.2.3 相似三角形应用举例(2)1. 能够利用相似三角形的知识,求出不能直接测量
的物体的高度和宽度. (重点)
2. 进一步了解数学建模思想,能够将实际问题转化
为相似三角形的数学模型,提高分析问题、解决
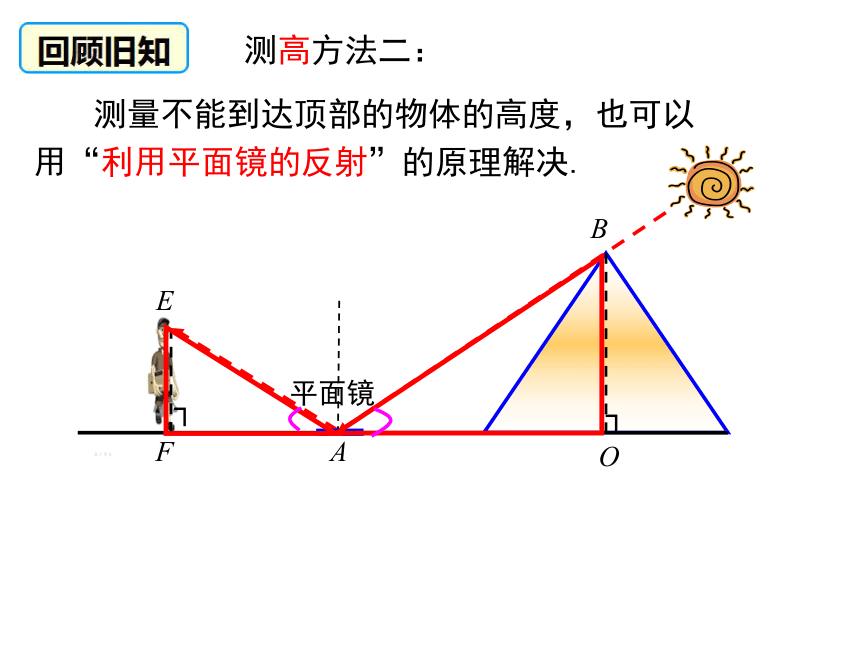
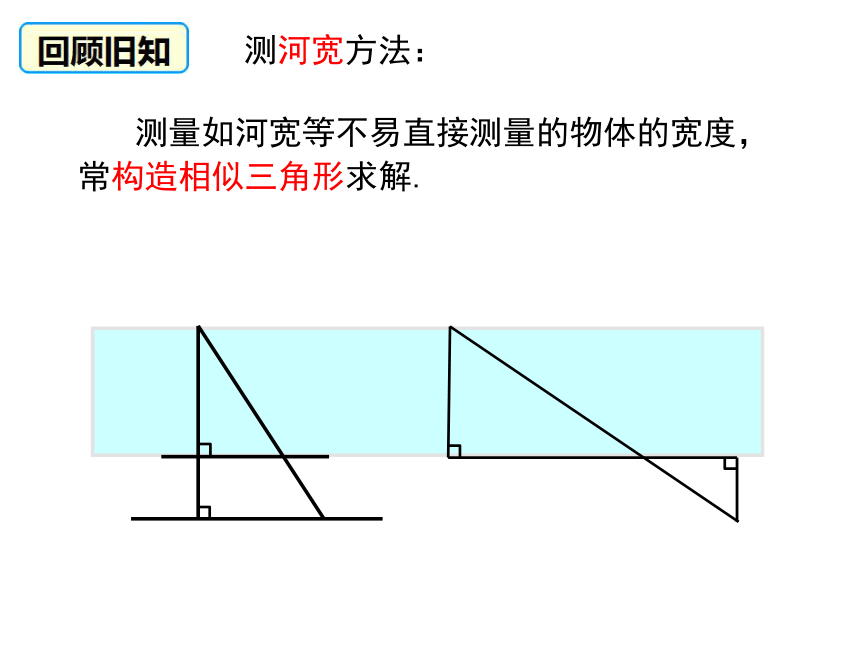
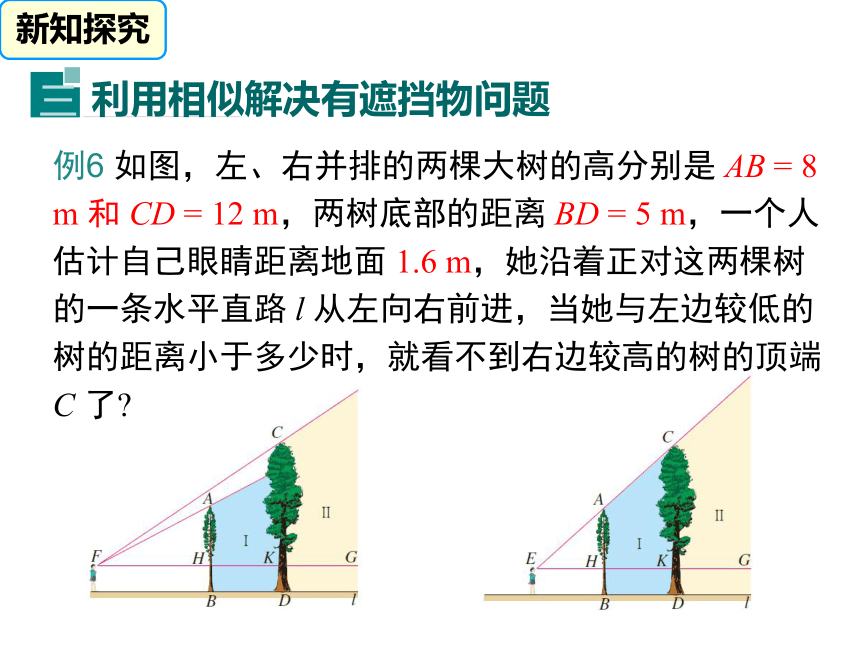
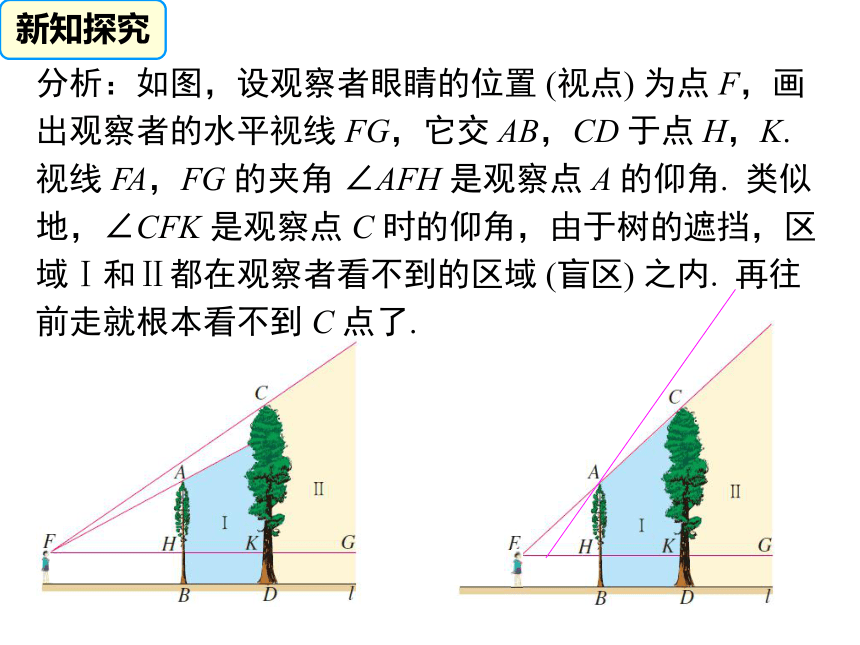
问题的能力. (难点)学习目标表达式:物1高 :物2高 = 影1长 :影2长测高方法一: 测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决. AFEBO┐┐平面镜测高方法二: 测量不能到达顶部的物体的高度,也可以用“利用平面镜的反射”的原理解决. 测量如河宽等不易直接测量的物体的宽度,常构造相似三角形求解. 测河宽方法:例6 如图,左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树底部的距离 BD = 5 m,一个人估计自己眼睛距离地面 1.6 m,她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了? 新知探究分析:如图,设观察者眼睛的位置 (视点) 为点 F,画出观察者的水平视线 FG,它交 AB,CD 于点 H,K.
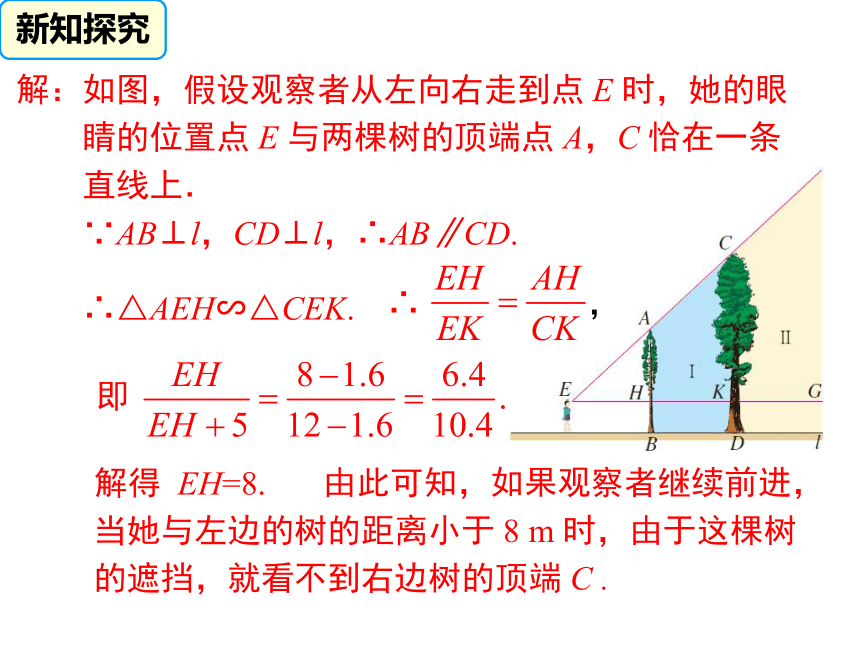
视线 FA,FG 的夹角 ∠AFH 是观察点 A 的仰角. 类似地,∠CFK 是观察点 C 时的仰角,由于树的遮挡,区域Ⅰ和Ⅱ都在观察者看不到的区域 (盲区) 之内. 再往前走就根本看不到 C 点了.新知探究 由此可知,如果观察者继续前进,
当她与左边的树的距离小于 8 m 时,由于这棵树
的遮挡,就看不到右边树的顶端 C . 解:如图,假设观察者从左向右走到点 E 时,她的眼
睛的位置点 E 与两棵树的顶端点 A,C 恰在一条
直线上.
∵AB⊥l,CD⊥l,∴AB∥CD.
∴△AEH∽△CEK.解得 EH=8.新知探究BB’1、(1)小明测得长为1米的竹竿影长为0.9米,同时,小明测得一棵树的影长为5.4米,请计算小明测量这棵树的高. 5.4ACA’C’跟踪训练 (2) 小明测得长为1米的竹竿影长为0.9米, 同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2mBACD2.7m1.2mBAC解法一:作CG⊥AB于G, CG=BD=2.7,BG=CD=1.2 答:这棵树的高为4.2米.
DG10.9∽习题精讲2.7m1.2m解法二:如图,过点D作DE∥AC交AB于E点,AE=CD=1.2,BADCE∽习题精讲 答:这棵树的高为4.2米.
2.7m1.2mBAC解法三:延长AC交BD延长线于G, 答:这棵树的高为4.2米.
DG∽∽习题精讲例7 如图所示,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到G点,DG=5米,这时小明的影长GH=5米,如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米)新知探究(请暂停,作答7分钟,播放看答案)相似三角形的应用举例利用相似三角形测量高度利用相似三角形测量宽度利用相似解决有遮挡物问题课堂小结方法:构造相似三角形,利用相似三角形的性质,对应边成比例,来解决实际问题。1.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的垂直距离CD为( )
A.0.2 m B.0.3 m
C.0.4 m D.0.5 m家庭作业2.小明在一次军事夏令营活动中,进行打靶训练,在用枪瞄准目标点B时,要使眼睛O、准星A、目标B在同一条直线上,如图所示,在射击时,小明在轻微的抖动,致使准星A偏离到A′,若OA=0.2 m,OB=40 m,AA′=0.001 5 m,则小明射击到的点B′偏离目标点B的长度BB′为( )
A.3 m B.0.3 m
C.0.03 m D.0.2 m家庭作业家庭作业3.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB= m.家庭作业4.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1 m的竹竿的影长为0.4 m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2 m,一级台阶高为0.3 m,如图所示,若此时落在地面上的影长为4.4 m,则树高为( )
A.11.5 m B.11.75 m
C.11.8 m D.12.25 m5.如图,为了求出海岛上的山峰AB的高度,在D处和F处树立标杆CD和EF,标杆的高都是3丈,D,F两处相隔100(1丈=10尺,1步=6尺),并且AB,CD和EF在同一平面内.从标杆CD后退123步的G处,可以看到顶峰A和标杆顶端C在一条直线上;从标杆EF后退127步的H处,可以看到顶峰A和标杆顶端E在一条直线上.求山峰的高度AB及它和标杆CD的水平距离BD各是多少步?(提示:连接并延长交AB于点K,用,AK与常数的积表示KC和KE.)家庭作业
的物体的高度和宽度. (重点)
2. 进一步了解数学建模思想,能够将实际问题转化
为相似三角形的数学模型,提高分析问题、解决
问题的能力. (难点)学习目标表达式:物1高 :物2高 = 影1长 :影2长测高方法一: 测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决. AFEBO┐┐平面镜测高方法二: 测量不能到达顶部的物体的高度,也可以用“利用平面镜的反射”的原理解决. 测量如河宽等不易直接测量的物体的宽度,常构造相似三角形求解. 测河宽方法:例6 如图,左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树底部的距离 BD = 5 m,一个人估计自己眼睛距离地面 1.6 m,她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了? 新知探究分析:如图,设观察者眼睛的位置 (视点) 为点 F,画出观察者的水平视线 FG,它交 AB,CD 于点 H,K.
视线 FA,FG 的夹角 ∠AFH 是观察点 A 的仰角. 类似地,∠CFK 是观察点 C 时的仰角,由于树的遮挡,区域Ⅰ和Ⅱ都在观察者看不到的区域 (盲区) 之内. 再往前走就根本看不到 C 点了.新知探究 由此可知,如果观察者继续前进,
当她与左边的树的距离小于 8 m 时,由于这棵树
的遮挡,就看不到右边树的顶端 C . 解:如图,假设观察者从左向右走到点 E 时,她的眼
睛的位置点 E 与两棵树的顶端点 A,C 恰在一条
直线上.
∵AB⊥l,CD⊥l,∴AB∥CD.
∴△AEH∽△CEK.解得 EH=8.新知探究BB’1、(1)小明测得长为1米的竹竿影长为0.9米,同时,小明测得一棵树的影长为5.4米,请计算小明测量这棵树的高. 5.4ACA’C’跟踪训练 (2) 小明测得长为1米的竹竿影长为0.9米, 同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2mBACD2.7m1.2mBAC解法一:作CG⊥AB于G, CG=BD=2.7,BG=CD=1.2 答:这棵树的高为4.2米.
DG10.9∽习题精讲2.7m1.2m解法二:如图,过点D作DE∥AC交AB于E点,AE=CD=1.2,BADCE∽习题精讲 答:这棵树的高为4.2米.
2.7m1.2mBAC解法三:延长AC交BD延长线于G, 答:这棵树的高为4.2米.
DG∽∽习题精讲例7 如图所示,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到G点,DG=5米,这时小明的影长GH=5米,如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米)新知探究(请暂停,作答7分钟,播放看答案)相似三角形的应用举例利用相似三角形测量高度利用相似三角形测量宽度利用相似解决有遮挡物问题课堂小结方法:构造相似三角形,利用相似三角形的性质,对应边成比例,来解决实际问题。1.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的垂直距离CD为( )
A.0.2 m B.0.3 m
C.0.4 m D.0.5 m家庭作业2.小明在一次军事夏令营活动中,进行打靶训练,在用枪瞄准目标点B时,要使眼睛O、准星A、目标B在同一条直线上,如图所示,在射击时,小明在轻微的抖动,致使准星A偏离到A′,若OA=0.2 m,OB=40 m,AA′=0.001 5 m,则小明射击到的点B′偏离目标点B的长度BB′为( )
A.3 m B.0.3 m
C.0.03 m D.0.2 m家庭作业家庭作业3.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB= m.家庭作业4.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1 m的竹竿的影长为0.4 m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2 m,一级台阶高为0.3 m,如图所示,若此时落在地面上的影长为4.4 m,则树高为( )
A.11.5 m B.11.75 m
C.11.8 m D.12.25 m5.如图,为了求出海岛上的山峰AB的高度,在D处和F处树立标杆CD和EF,标杆的高都是3丈,D,F两处相隔100(1丈=10尺,1步=6尺),并且AB,CD和EF在同一平面内.从标杆CD后退123步的G处,可以看到顶峰A和标杆顶端C在一条直线上;从标杆EF后退127步的H处,可以看到顶峰A和标杆顶端E在一条直线上.求山峰的高度AB及它和标杆CD的水平距离BD各是多少步?(提示:连接并延长交AB于点K,用,AK与常数的积表示KC和KE.)家庭作业
