人教版九年级数学下册27.3位似课件(第2课时 共25张PPT)
文档属性
| 名称 | 人教版九年级数学下册27.3位似课件(第2课时 共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 238.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 22:10:06 | ||
图片预览





文档简介
课件25张PPT。27.3.1 位似(2)学习目标1. 理解平面直角坐标系中,位似图形对应
点的坐标之间的联系.
2. 能够熟练准确地利用坐标变化将一个图
形放大与缩小.回顾旧知二、位似图形的性质:
1、位似图形一定是相似图形,具有形似图形的所有性质。
2、位似图形对应点连线相交于一点。
3、位似图形的对应边平行或在一条直线上。
4、位似图形中任意一对对应点到位似中心的距离之比等于位似比。 一、位似图形的概念:
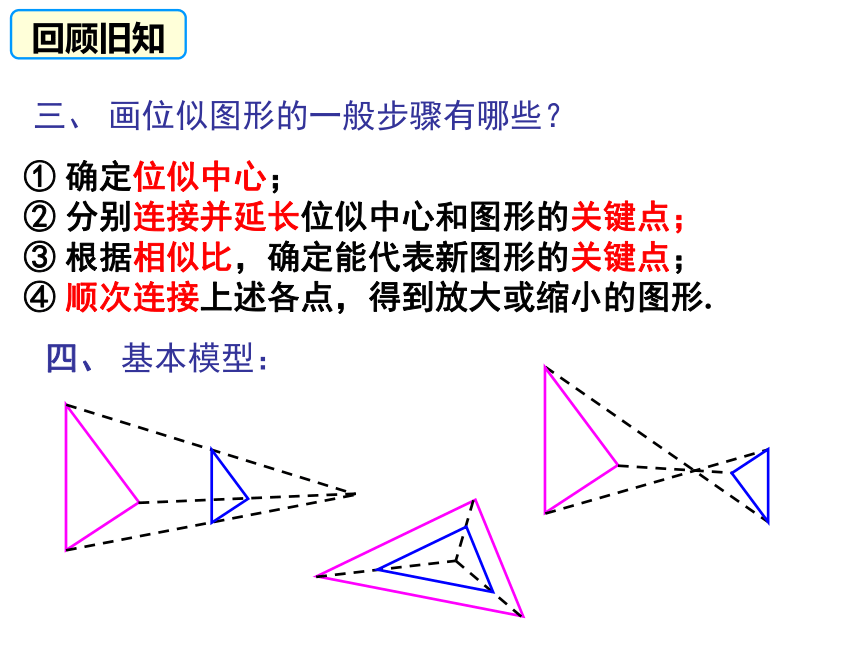
两个相似多边形,如果它们对应顶点所在的直线相交于一点,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心.三、 画位似图形的一般步骤有哪些?四、 基本模型:① 确定位似中心;
② 分别连接并延长位似中心和图形的关键点;
③ 根据相似比,确定能代表新图形的关键点;
④ 顺次连接上述各点,得到放大或缩小的图形.回顾旧知在平面直角坐标系中,平移变换的方法:左右平移,横坐标左减右加;上下平移,纵坐标上加下减。1、将点A(2,3)向右平移2个单位,再向下平移5个单位得到点B,则点B的坐标是______。2、在平面直角坐标系中,点A(2,3)关于x轴的对称点是_________,点A关于y轴的对称点是________,点A关于原点的对称点是_________。在平面直角坐标系中,
两点关于x轴对称:横坐标相同,纵坐标相反。
两点关于y轴对称:横坐标相反,纵坐标相同。
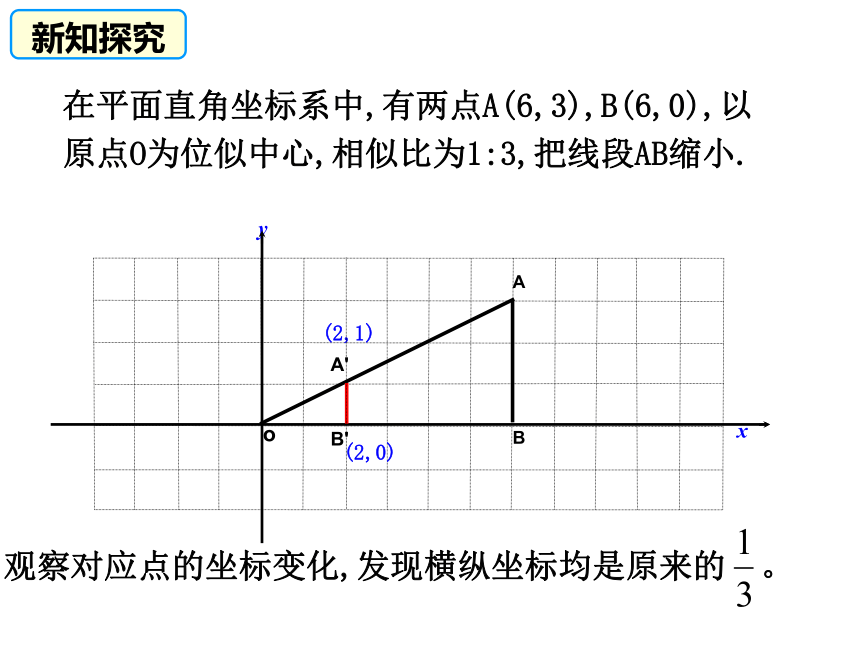
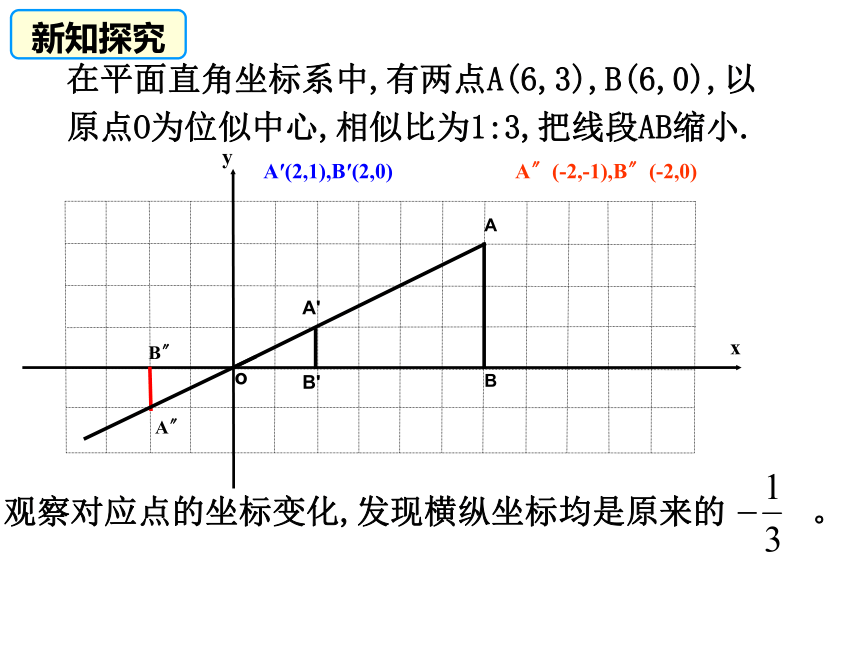
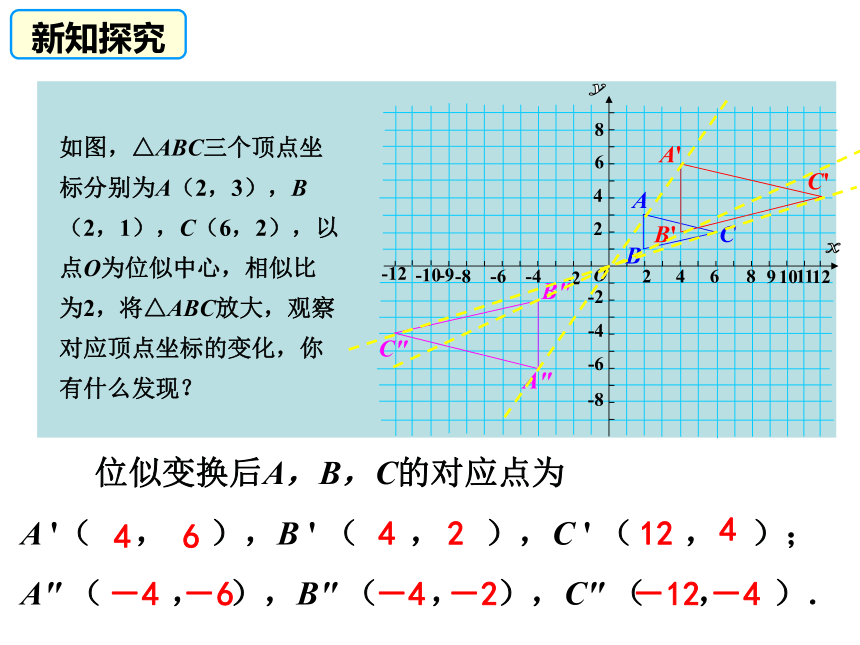
两点关于原点对称:横纵坐标都相反。回顾旧知,类比引入(4,-2)(2,-3)(-2,3)(-2,-3) 我们知道,在直角坐标系中,平移、轴对称和旋转 (中心对称)的点的坐标关系中有一定的规律. 那么,平面直角坐标系中,位似图形的对应点坐标是否也有一定的规律呢?引入新知B'A'xyBAo在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.(2,1)观察对应点的坐标变化,发现横纵坐标均是原来的 。(2,0)新知探究B'A'xyBAo在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.A′(2,1),B′(2,0)A〞B〞A〞(-2,-1),B〞(-2,0)新知探究观察对应点的坐标变化,发现横纵坐标均是原来的 。如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?ABC 位似变换后A,B,C的对应点为
A '( , ),B ' ( , ),C ' ( , );
A" ( , ),B" ( , ),C" ( , ).4642124-4-6-4-2-4-12A'B'C'A"B"C"新知探究在平面直角坐标系中,如果位似变换是以原点为位似中心,
相似比为k,那么位似图形对应点的坐标的比等于k或-k.结论:在平面直角坐标系中, 以原点O为位似中心,位似比为k,若原图形上点A的坐标为(x,y),那么位似图形对应点A’的坐标为(kx,ky)或(-kx,-ky)归纳整理典例精析例1 如图,在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形使它与 △ABO 的相似比为 3 : 2.解:利用位似中对应点的坐标的变化规律,先分别找到A(-2,4),B(-2,0),O(0,0),横纵坐标均乘以 , 得到对应点坐标 A′ (-3,6),B′ (-3,0),O (0,0).A′B′顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.A′B′横坐标:纵坐标:同理可得B??(3,0),O(0,0)A′′B′′根据相同位似比得到的两个图形关于原点成中心对称 在平面直角坐标系中,四边形 OABC 的顶点坐标分别为 O (0,0),A (6,0),B (3,6),C (-3,3). 以原点 O 为位似中心,画出四边形 OABC 的位似图形,使它与四边形 OABC 的相似比是 2 : 3.练一练OC24646B'-2-4-4xyABA'C'OC24646B″-2-4-4xyABA″C″ 如图,小朋在坐标系中以A为位似中心画了两个位
似的直角三角形,可不小心把 E 点弄脏了,则 E
点坐标为 ( )
A.(4,-3) B.(4,-2)
C.(4,-4) D.(4,-6) 拓展延伸A平面直角坐标系中的位似平面直角坐标系中的位似变换平面直角坐标系中的图形变换坐标变化规律平面直角坐标系中的位似图形的画法在平面直角坐标系中, 以原点O为位似中心,位似比为k,若原图形上点A的坐标为(x,y),那么位似图形对应点A’的坐标为(kx,ky)或(-kx,-ky)课堂小结先根据变化规律计算出对应点的坐标,然后描点并顺次连接。平移,轴对称,旋转(中心对称),位似1. 将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是 ( )
A. 将各点的纵坐标乘以 2,横坐标不变
B. 将各点的横坐标除以 2,纵坐标不变
C. 将各点的横坐标、纵坐标都乘以 2
D. 将各点的纵坐标减去 2,横坐标加上 2 家庭作业2. 原点 O 是 △ABC 和 △A′B′C′ 的位似中心,点 A
(1,0) 与点 A′ (-2,0) 是对应点,△ABC 的面积
是 ,则 △A′B′C′ 的面积是 .家庭作业3. 如图所示,某学习小组在讨论 “变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点 (a,b) 对应大鱼上的点 .家庭作业4. 如图,正方形 ABCD 和正方形 OEFG 中,点 A 和
点 F 的坐标分别为 (3,2),(-1,-1),则两个正
方形的位似中心的坐标是___________________.x家庭作业 5.将图中的 △ABC 做下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.
(1) 沿 y 轴正向平移 3 个单位长度;
(2) 关于 x 轴对称;
(3) 以 C 为位似中心,将
△ABC 放大2倍;
(4) 以 C 为中心,将
△ABC 顺时针旋
转180°. 家庭作业6. 如图,点 A 的坐标为 (3,4),点 O 的坐标为 (0,0),
点 B 的坐标为 (4,0).(1) 将 △AOB 沿 x 轴向左平移
1 个单位长度后得△A1O1B1,
则点 A1 的坐标为 ,
△A1O1B1的面积为 ;(2) 将 △AOB 绕原点旋转 180°
后得 △A2O2B2,则点 A2 的
坐标为 ;家庭作业(3) 将 △AOB 沿 x 轴翻折后得 △A3O3B3,则点 A3 的
坐标为 ;(4) 以 O 为位似中心,按比例尺 1 : 2 将 △AOB 放大
后得 △A4O4B4,若点 B 在 x 轴负半轴上,则点 A4
的坐标为 ,△A4O4B4的面积为 .家庭作业
点的坐标之间的联系.
2. 能够熟练准确地利用坐标变化将一个图
形放大与缩小.回顾旧知二、位似图形的性质:
1、位似图形一定是相似图形,具有形似图形的所有性质。
2、位似图形对应点连线相交于一点。
3、位似图形的对应边平行或在一条直线上。
4、位似图形中任意一对对应点到位似中心的距离之比等于位似比。 一、位似图形的概念:
两个相似多边形,如果它们对应顶点所在的直线相交于一点,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心.三、 画位似图形的一般步骤有哪些?四、 基本模型:① 确定位似中心;
② 分别连接并延长位似中心和图形的关键点;
③ 根据相似比,确定能代表新图形的关键点;
④ 顺次连接上述各点,得到放大或缩小的图形.回顾旧知在平面直角坐标系中,平移变换的方法:左右平移,横坐标左减右加;上下平移,纵坐标上加下减。1、将点A(2,3)向右平移2个单位,再向下平移5个单位得到点B,则点B的坐标是______。2、在平面直角坐标系中,点A(2,3)关于x轴的对称点是_________,点A关于y轴的对称点是________,点A关于原点的对称点是_________。在平面直角坐标系中,
两点关于x轴对称:横坐标相同,纵坐标相反。
两点关于y轴对称:横坐标相反,纵坐标相同。
两点关于原点对称:横纵坐标都相反。回顾旧知,类比引入(4,-2)(2,-3)(-2,3)(-2,-3) 我们知道,在直角坐标系中,平移、轴对称和旋转 (中心对称)的点的坐标关系中有一定的规律. 那么,平面直角坐标系中,位似图形的对应点坐标是否也有一定的规律呢?引入新知B'A'xyBAo在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.(2,1)观察对应点的坐标变化,发现横纵坐标均是原来的 。(2,0)新知探究B'A'xyBAo在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.A′(2,1),B′(2,0)A〞B〞A〞(-2,-1),B〞(-2,0)新知探究观察对应点的坐标变化,发现横纵坐标均是原来的 。如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?ABC 位似变换后A,B,C的对应点为
A '( , ),B ' ( , ),C ' ( , );
A" ( , ),B" ( , ),C" ( , ).4642124-4-6-4-2-4-12A'B'C'A"B"C"新知探究在平面直角坐标系中,如果位似变换是以原点为位似中心,
相似比为k,那么位似图形对应点的坐标的比等于k或-k.结论:在平面直角坐标系中, 以原点O为位似中心,位似比为k,若原图形上点A的坐标为(x,y),那么位似图形对应点A’的坐标为(kx,ky)或(-kx,-ky)归纳整理典例精析例1 如图,在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形使它与 △ABO 的相似比为 3 : 2.解:利用位似中对应点的坐标的变化规律,先分别找到A(-2,4),B(-2,0),O(0,0),横纵坐标均乘以 , 得到对应点坐标 A′ (-3,6),B′ (-3,0),O (0,0).A′B′顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.A′B′横坐标:纵坐标:同理可得B??(3,0),O(0,0)A′′B′′根据相同位似比得到的两个图形关于原点成中心对称 在平面直角坐标系中,四边形 OABC 的顶点坐标分别为 O (0,0),A (6,0),B (3,6),C (-3,3). 以原点 O 为位似中心,画出四边形 OABC 的位似图形,使它与四边形 OABC 的相似比是 2 : 3.练一练OC24646B'-2-4-4xyABA'C'OC24646B″-2-4-4xyABA″C″ 如图,小朋在坐标系中以A为位似中心画了两个位
似的直角三角形,可不小心把 E 点弄脏了,则 E
点坐标为 ( )
A.(4,-3) B.(4,-2)
C.(4,-4) D.(4,-6) 拓展延伸A平面直角坐标系中的位似平面直角坐标系中的位似变换平面直角坐标系中的图形变换坐标变化规律平面直角坐标系中的位似图形的画法在平面直角坐标系中, 以原点O为位似中心,位似比为k,若原图形上点A的坐标为(x,y),那么位似图形对应点A’的坐标为(kx,ky)或(-kx,-ky)课堂小结先根据变化规律计算出对应点的坐标,然后描点并顺次连接。平移,轴对称,旋转(中心对称),位似1. 将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是 ( )
A. 将各点的纵坐标乘以 2,横坐标不变
B. 将各点的横坐标除以 2,纵坐标不变
C. 将各点的横坐标、纵坐标都乘以 2
D. 将各点的纵坐标减去 2,横坐标加上 2 家庭作业2. 原点 O 是 △ABC 和 △A′B′C′ 的位似中心,点 A
(1,0) 与点 A′ (-2,0) 是对应点,△ABC 的面积
是 ,则 △A′B′C′ 的面积是 .家庭作业3. 如图所示,某学习小组在讨论 “变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点 (a,b) 对应大鱼上的点 .家庭作业4. 如图,正方形 ABCD 和正方形 OEFG 中,点 A 和
点 F 的坐标分别为 (3,2),(-1,-1),则两个正
方形的位似中心的坐标是___________________.x家庭作业 5.将图中的 △ABC 做下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.
(1) 沿 y 轴正向平移 3 个单位长度;
(2) 关于 x 轴对称;
(3) 以 C 为位似中心,将
△ABC 放大2倍;
(4) 以 C 为中心,将
△ABC 顺时针旋
转180°. 家庭作业6. 如图,点 A 的坐标为 (3,4),点 O 的坐标为 (0,0),
点 B 的坐标为 (4,0).(1) 将 △AOB 沿 x 轴向左平移
1 个单位长度后得△A1O1B1,
则点 A1 的坐标为 ,
△A1O1B1的面积为 ;(2) 将 △AOB 绕原点旋转 180°
后得 △A2O2B2,则点 A2 的
坐标为 ;家庭作业(3) 将 △AOB 沿 x 轴翻折后得 △A3O3B3,则点 A3 的
坐标为 ;(4) 以 O 为位似中心,按比例尺 1 : 2 将 △AOB 放大
后得 △A4O4B4,若点 B 在 x 轴负半轴上,则点 A4
的坐标为 ,△A4O4B4的面积为 .家庭作业
