2020春北师大版七下数学4.3探索三角形全等的条件教学课件(19张ppt)
文档属性
| 名称 | 2020春北师大版七下数学4.3探索三角形全等的条件教学课件(19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 366.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 09:24:19 | ||
图片预览






文档简介
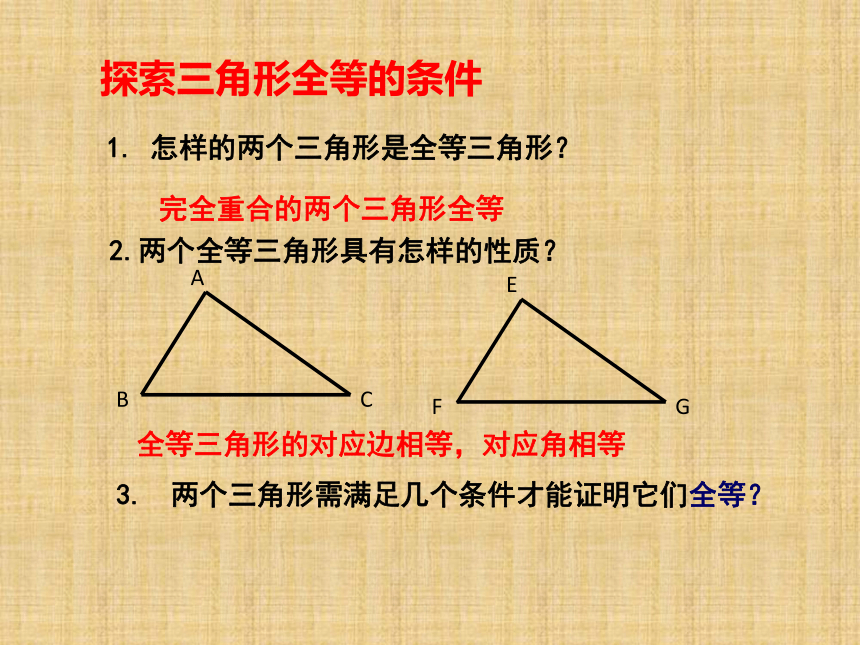
课件19张PPT。4.3 探索三角形全等的条件第三章 三角形1. 怎样的两个三角形是全等三角形?2.两个全等三角形具有怎样的性质?3. 两个三角形需满足几个条件才能证明它们全等?探索三角形全等的条件 全等三角形的对应边相等,对应角相等完全重合的两个三角形全等 两个条件 (1) 三角形的一个角 ,一条边对应相等(2)三角形的两条边对应相等
(3)三角形的两个角对应相等一个条件(1)有一条边对应相等的三角形(2)有一个角对应相等的三角形只给出一个或两个条件时,都不能保证所画的三角形
一定全等.完成课本做一做(1) 三角形的三个角对应相等.三个条件(2) 三角形的三条边对应相等.给出三个条件时, 三个内角对应相等的两个三角形也不一定全等.(3) 三角形的两边一角对应相等.(4) 三角形的两角一边对应相等.画一画用刻度尺和圆规画一个三角形,使它的三条边长分别是2cm,3cm,4cm.1. 画线段AB=2cm.画法:2. 分别以A,B为圆心,3cm,4cm长为
半径 画两条圆弧,交于点C.3. 连结CA,AB. 与同伴比一比,发现什么? 三角形全等的条件 有三条边对应相等的两个三角形全等记做“边边边”或“SSS”做一做 有一些长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们. 三角形的大小和形状是固定不变的,而四边形的形状会改变. 只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫三角形的稳定性. 欣赏生活中的三角形1.如何判断老师在一张纸上画的这两个三角形是否全等?量一量AB= 4CM
BC=6CM
AC= 5.4CM EF=4CM
FG=6CM
EG=5.4CM∵ AB=EF,BC=FG,AC=EGBCBC△DCB2、填空题:解: △ABC≌△DCB
理由如下:
AB = CD
∵ AC = BD
= ∴ △ABC ≌ ( ) SSS 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由. 例2.如图,仪器ABCD可以用来平分一个角,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们落在角的两边上,沿AC画一条射线AE,AE就是∠PRQ的平分线.你能说明其中的道理吗?小明的思考过程如下:AB=ADBC=DCAC=ACΔABC≌ΔADC∠QRE=∠PRE你能说出每一步的理由吗?知识回顾1. 已知三边长画三角形的方法;2. 三角形全等条件;3. 三角形的稳定性.
(3)三角形的两个角对应相等一个条件(1)有一条边对应相等的三角形(2)有一个角对应相等的三角形只给出一个或两个条件时,都不能保证所画的三角形
一定全等.完成课本做一做(1) 三角形的三个角对应相等.三个条件(2) 三角形的三条边对应相等.给出三个条件时, 三个内角对应相等的两个三角形也不一定全等.(3) 三角形的两边一角对应相等.(4) 三角形的两角一边对应相等.画一画用刻度尺和圆规画一个三角形,使它的三条边长分别是2cm,3cm,4cm.1. 画线段AB=2cm.画法:2. 分别以A,B为圆心,3cm,4cm长为
半径 画两条圆弧,交于点C.3. 连结CA,AB. 与同伴比一比,发现什么? 三角形全等的条件 有三条边对应相等的两个三角形全等记做“边边边”或“SSS”做一做 有一些长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们. 三角形的大小和形状是固定不变的,而四边形的形状会改变. 只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫三角形的稳定性. 欣赏生活中的三角形1.如何判断老师在一张纸上画的这两个三角形是否全等?量一量AB= 4CM
BC=6CM
AC= 5.4CM EF=4CM
FG=6CM
EG=5.4CM∵ AB=EF,BC=FG,AC=EGBCBC△DCB2、填空题:解: △ABC≌△DCB
理由如下:
AB = CD
∵ AC = BD
= ∴ △ABC ≌ ( ) SSS 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由. 例2.如图,仪器ABCD可以用来平分一个角,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们落在角的两边上,沿AC画一条射线AE,AE就是∠PRQ的平分线.你能说明其中的道理吗?小明的思考过程如下:AB=ADBC=DCAC=ACΔABC≌ΔADC∠QRE=∠PRE你能说出每一步的理由吗?知识回顾1. 已知三边长画三角形的方法;2. 三角形全等条件;3. 三角形的稳定性.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
