苏科版九年级下册数学课件6.6图形的位似 (共29张ppt) 使用WPS打开
文档属性
| 名称 | 苏科版九年级下册数学课件6.6图形的位似 (共29张ppt) 使用WPS打开 |  | |
| 格式 | zip | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-15 11:53:03 | ||
图片预览




文档简介
(共29张PPT)
①
②
③
④
⑤
.
.
E
F
6.6图形的位似
1. 前面我们已经学习了图形的哪些变换?
平移:平移的方向,平移的距离.
注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
回顾与反思
下面请欣赏如下图形的变换
旋转:(中心对称)旋转中心,旋转方向,旋转角度.
翻折:对称轴
①
②
下面两副图是相似形吗?认真观察看它们还有什么特征?
A
B
C
D
E
F
O
M
N
探索活动
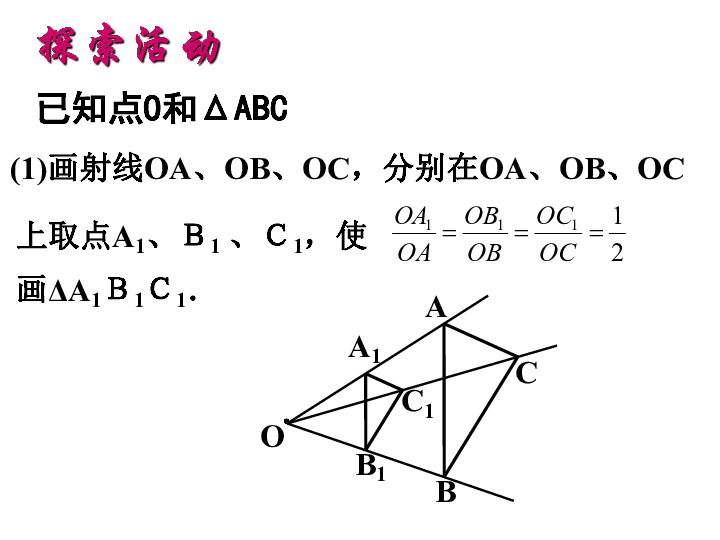
已知点O和ΔABC
(1)画射线OA、OB、OC,分别在OA、OB、OC
画ΔA1B1C1.
上取点A1、B1 、C1,使
A1
B1
C1
A
B
C
O
.
已知点O和ΔABC
分别在OA、OB、OC的反向延长线上取点A2、
B2、C2,使
,画ΔA2B2C2.
B
.
A
C
O
A2
B2
C2
探索活动
观察与思考
?
两个多边形的顶点A与A’、B与B’、C与C’······所在的直线都经过同一点O,并且
像这样的两个多边形叫做位似多边形,点O叫做位似中心.
①
②
③
④
⑤
.
.
E
F
放电影时,胶片和屏幕上的画面就形成了一种位似关系
利用位似的方法,可以把一个多边形放大或缩小.
想一想
ΔABC与ΔA'B'C'是位似形,两个三角形相似吗?它们的对应边有怎样的位置关系?为什么?
想一想
四边形ABCD与四边形A‘B’C‘D’是位似形,两个四边形相似吗?它们的对应边有怎样的位置关系?为什么?
总结与归纳
位似的特征
1.两个位似多边形一定相似,
2.对应边互相平行(或在同一直线上)
3.对应顶点所在直线都经过位似中心
4.各对应顶点到位似中心距离的比等于相似比
位似变换的作用
可以把一个图形放大或缩小(画相似图形)
判断下面的正方形是不是位似图形?
想一想
(1)
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
这两个相似图形是位似图形吗?
这两个相似图形是位似图形吗?
△ABC与△ADE
①DE∥BC
②∠AED=∠B
判断下列各对图形哪些是位似图形,哪些不是. 为什么?
是
不是
3.位似多边形一定是相似多边形吗?
反过来呢?
位似多边形一定是相似多边形,
相似多边形不一定是位似多边形,
议一议
?
2. 位似多边形定义即性质
(2)位似多边形上任意一对对应点到位似中心的距离之比等于相似比.
(3)位似多边形中的对应线段平行(或在一条直线上).
(1)位似多边形是相似多边形,
你能作出下列位似图形的位似中心吗?:
O
O
想一想
O
.
A
B
C
.
二.利用位似放缩图形
如图,已知△ABC和点O.以O为位似中心,画△ABC的位似图形,使它与△ABC的相似比为2.
B’
A'
C’
如何对一个图形进行放大或缩小呢?
还有没有其他作法?
O
.
A
B
C
思考:
2.如果位似中心在三角形内部呢?
A'
C’
B’
1.用上面的方法画出的三角形为何与△ABC相似?
作位似图形的步骤:
第一步:在原图上找若干个关键点,并任取一点作为位似中心。
第二步:作位似中心与各关键点连线。
第三步:在连线上取关键点的对应点,使之满足放缩比例。
第四步:顺次连接截取点。
选点
连线
定对应点
连线
。
将黄色五角星缩小为原来的一半
。
。
。
。
。
。
。
。
。
。
O
1、下列说法不正确的是( )
A、位似图形一定是相似图形
B、相似图形不一定是位似图形
C、位似图形上任意一对对应点到位似中心的距离之比等于位似比
D、位似图形中每组对应点所在的直线必相互平行
能力挑战
D
2、如图,
与
是位似图形,
点O
是位似中心,若
,则
.
C’
O
A
B
C
A’
B’
OA:OA’=2:3
18
3、完成书第79页第二题
归纳总结:
1、位似图形的概念
2、位似图形的性质
3、利用位似图形可解决实际问题
可放大或缩小图形
两个多边形的顶点A与A’、B与B’、C与C’······所在的直线都经过同一点O,并且
像这样的两个多边形叫做位似多边形,点O叫做位似中心.
总结与归纳
位似的特征
1.两个位似多边形一定相似,
2.对应边互相平行(或在同一直线上)
3.对应顶点所在直线都经过位似中心
4.各对应顶点到位似中心距离的比等于相似比
位似变换的作用
可以把一个图形放大或缩小(画相似图形)
①
②
③
④
⑤
.
.
E
F
6.6图形的位似
1. 前面我们已经学习了图形的哪些变换?
平移:平移的方向,平移的距离.
注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
回顾与反思
下面请欣赏如下图形的变换
旋转:(中心对称)旋转中心,旋转方向,旋转角度.
翻折:对称轴
①
②
下面两副图是相似形吗?认真观察看它们还有什么特征?
A
B
C
D
E
F
O
M
N
探索活动
已知点O和ΔABC
(1)画射线OA、OB、OC,分别在OA、OB、OC
画ΔA1B1C1.
上取点A1、B1 、C1,使
A1
B1
C1
A
B
C
O
.
已知点O和ΔABC
分别在OA、OB、OC的反向延长线上取点A2、
B2、C2,使
,画ΔA2B2C2.
B
.
A
C
O
A2
B2
C2
探索活动
观察与思考
?
两个多边形的顶点A与A’、B与B’、C与C’······所在的直线都经过同一点O,并且
像这样的两个多边形叫做位似多边形,点O叫做位似中心.
①
②
③
④
⑤
.
.
E
F
放电影时,胶片和屏幕上的画面就形成了一种位似关系
利用位似的方法,可以把一个多边形放大或缩小.
想一想
ΔABC与ΔA'B'C'是位似形,两个三角形相似吗?它们的对应边有怎样的位置关系?为什么?
想一想
四边形ABCD与四边形A‘B’C‘D’是位似形,两个四边形相似吗?它们的对应边有怎样的位置关系?为什么?
总结与归纳
位似的特征
1.两个位似多边形一定相似,
2.对应边互相平行(或在同一直线上)
3.对应顶点所在直线都经过位似中心
4.各对应顶点到位似中心距离的比等于相似比
位似变换的作用
可以把一个图形放大或缩小(画相似图形)
判断下面的正方形是不是位似图形?
想一想
(1)
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
这两个相似图形是位似图形吗?
这两个相似图形是位似图形吗?
△ABC与△ADE
①DE∥BC
②∠AED=∠B
判断下列各对图形哪些是位似图形,哪些不是. 为什么?
是
不是
3.位似多边形一定是相似多边形吗?
反过来呢?
位似多边形一定是相似多边形,
相似多边形不一定是位似多边形,
议一议
?
2. 位似多边形定义即性质
(2)位似多边形上任意一对对应点到位似中心的距离之比等于相似比.
(3)位似多边形中的对应线段平行(或在一条直线上).
(1)位似多边形是相似多边形,
你能作出下列位似图形的位似中心吗?:
O
O
想一想
O
.
A
B
C
.
二.利用位似放缩图形
如图,已知△ABC和点O.以O为位似中心,画△ABC的位似图形,使它与△ABC的相似比为2.
B’
A'
C’
如何对一个图形进行放大或缩小呢?
还有没有其他作法?
O
.
A
B
C
思考:
2.如果位似中心在三角形内部呢?
A'
C’
B’
1.用上面的方法画出的三角形为何与△ABC相似?
作位似图形的步骤:
第一步:在原图上找若干个关键点,并任取一点作为位似中心。
第二步:作位似中心与各关键点连线。
第三步:在连线上取关键点的对应点,使之满足放缩比例。
第四步:顺次连接截取点。
选点
连线
定对应点
连线
。
将黄色五角星缩小为原来的一半
。
。
。
。
。
。
。
。
。
。
O
1、下列说法不正确的是( )
A、位似图形一定是相似图形
B、相似图形不一定是位似图形
C、位似图形上任意一对对应点到位似中心的距离之比等于位似比
D、位似图形中每组对应点所在的直线必相互平行
能力挑战
D
2、如图,
与
是位似图形,
点O
是位似中心,若
,则
.
C’
O
A
B
C
A’
B’
OA:OA’=2:3
18
3、完成书第79页第二题
归纳总结:
1、位似图形的概念
2、位似图形的性质
3、利用位似图形可解决实际问题
可放大或缩小图形
两个多边形的顶点A与A’、B与B’、C与C’······所在的直线都经过同一点O,并且
像这样的两个多边形叫做位似多边形,点O叫做位似中心.
总结与归纳
位似的特征
1.两个位似多边形一定相似,
2.对应边互相平行(或在同一直线上)
3.对应顶点所在直线都经过位似中心
4.各对应顶点到位似中心距离的比等于相似比
位似变换的作用
可以把一个图形放大或缩小(画相似图形)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
