人教版必修二物理 6.4-万有引力理论成就 (共39张PPT)
文档属性
| 名称 | 人教版必修二物理 6.4-万有引力理论成就 (共39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 804.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-09 16:19:29 | ||
图片预览






文档简介
(共39张PPT)
6.4万有引力理论成就
复习:
1、万有引力定律的内容是什么?
2、该定律的适用条件是什么?
3、引力常数G的单位?
万有引力与重力
1、不加说明,万有引力等于重力
2、考虑自转时,重力是万有引力的一个分力
一、天体质量的计算
利用星球表面重力加速度值,计算该星球质量。(不考虑星球自转的影响)
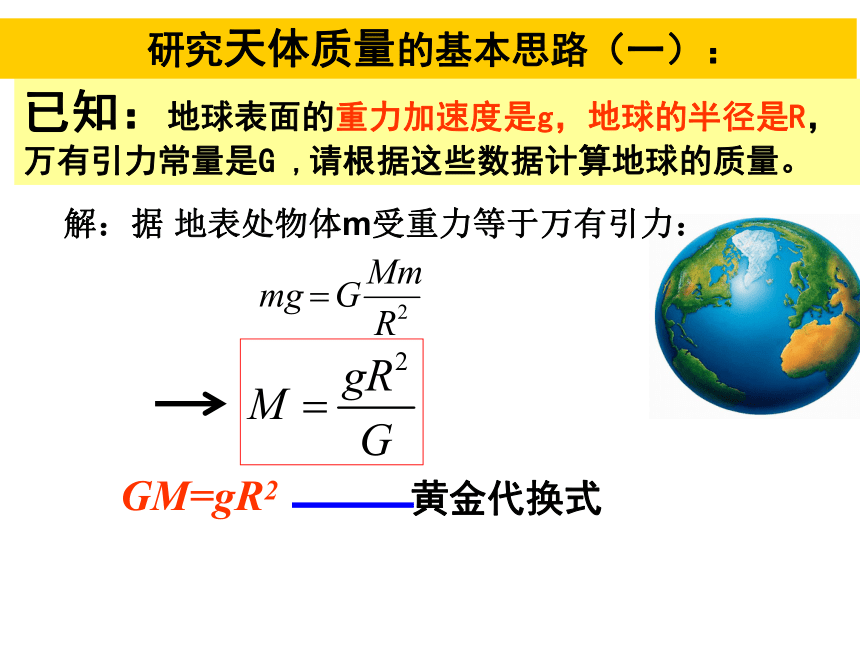
研究天体质量的基本思路(一):
地表处物体m受重力等于万有引力
方法
已知:地球表面的重力加速度是g,地球的半径是R,万有引力常量是G ,请根据这些数据计算地球的质量。
GM=gR2
解:据 地表处物体m受重力等于万有引力:
探究
研究天体质量的基本思路(一):
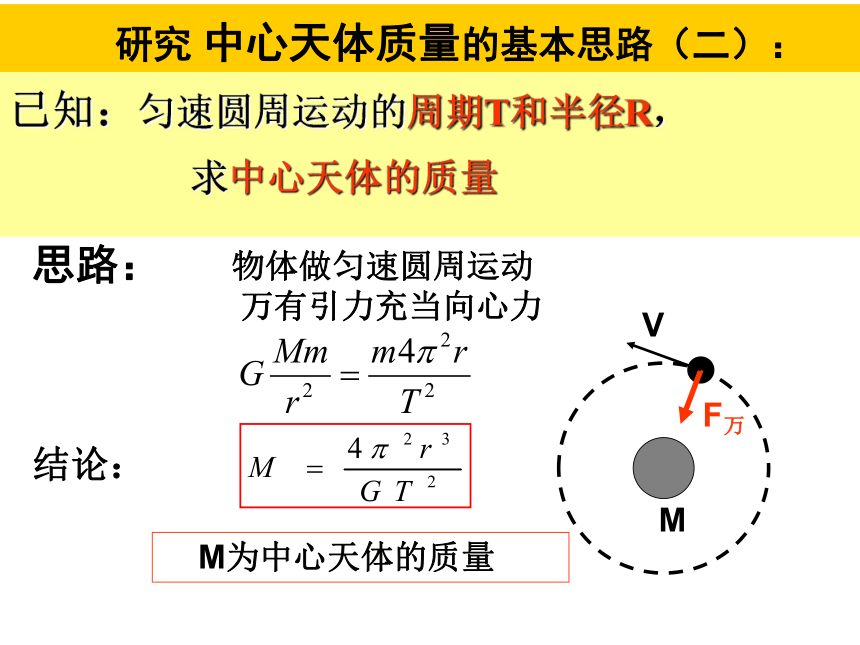
研究 中心天体质量的基本思路(二):
思路:
已知:匀速圆周运动的周期T和半径R,
求中心天体的质量
物体做匀速圆周运动
万有引力充当向心力
M
V
M为中心天体的质量
结论:
例一: 已知月球绕地球的周期是t,轨道
半径为a;地球绕太阳周期为T,轨道半径为b。
求:地球质量与太阳质量之比
据:
解得中心天体质量
所求比值:
找
通
式
法
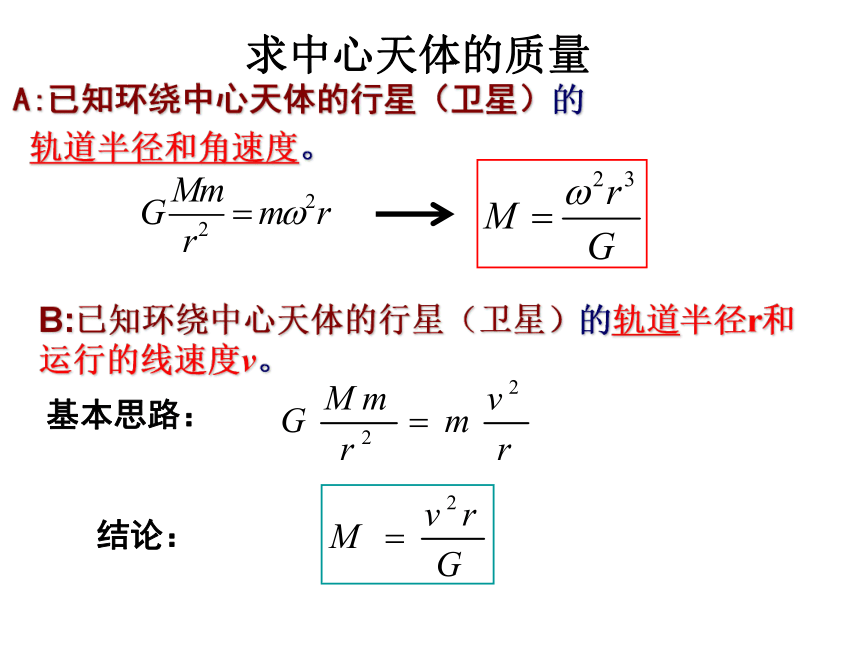
A:已知环绕中心天体的行星(卫星)的
轨道半径和角速度。
B:已知环绕中心天体的行星(卫星)的轨道半径r和运行的线速度v。
基本思路:
结论:
求中心天体的质量
思考:
已知天体质量如何求天体密度?
二、天体密度的计算
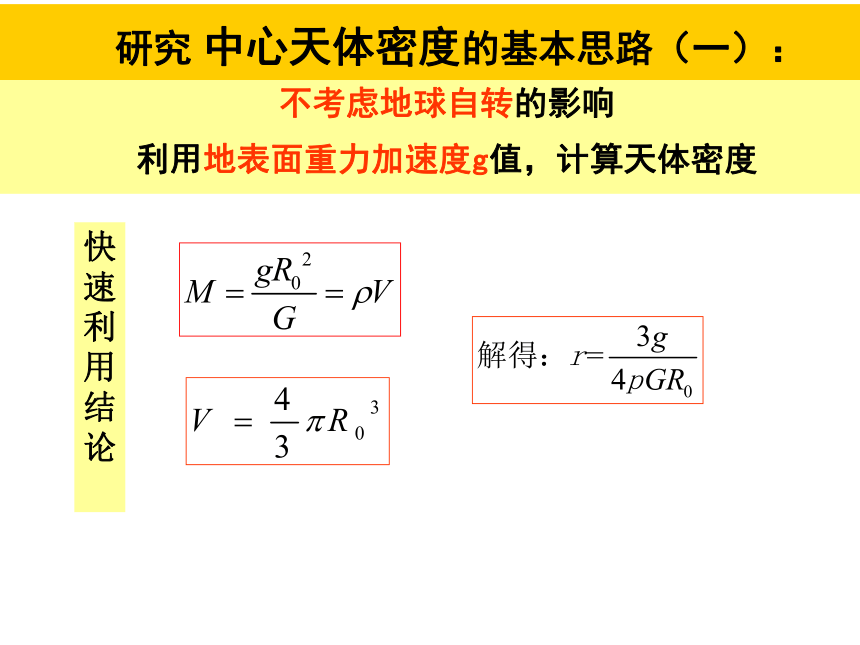
不考虑地球自转的影响
利用地表面重力加速度g值,计算天体密度
研究 中心天体密度的基本思路(一):
快
速
利
用
结
论
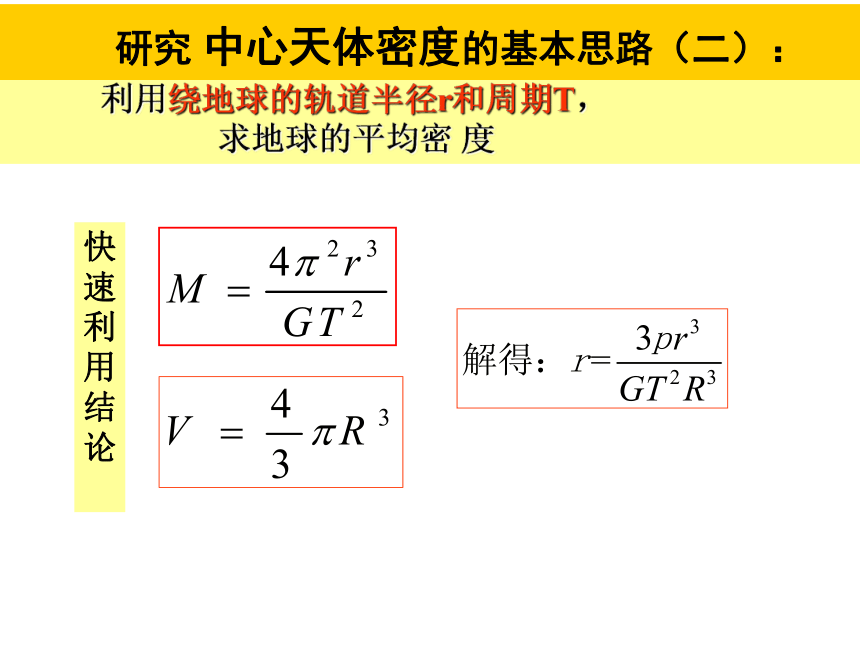
利用绕地球的轨道半径r和周期T,
求地球的平均密 度
研究 中心天体密度的基本思路(二):
快
速
利
用
结
论
讨论:若仅已知一个在地球表面附近运动的
卫星的周期,能否近似求得地球的密度?
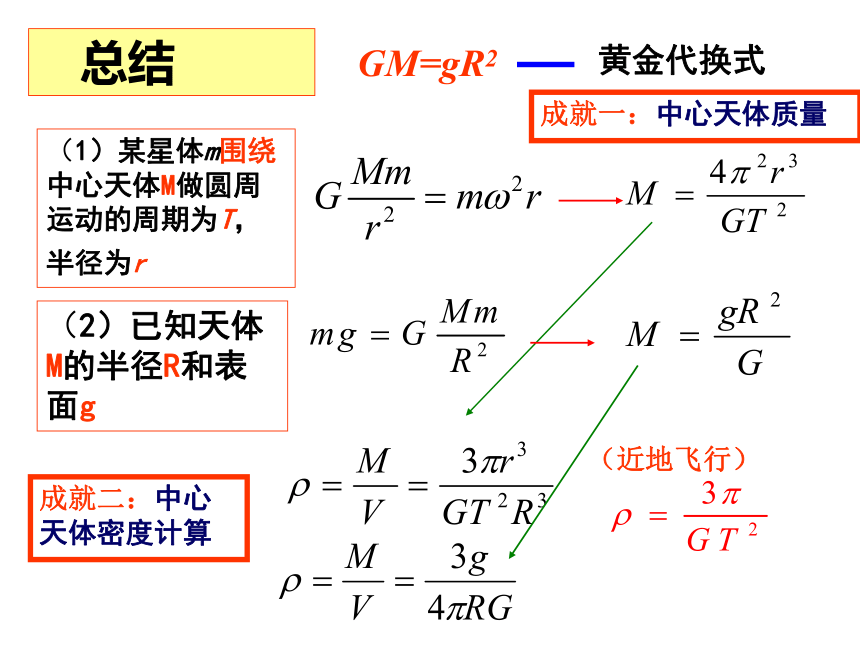
总结
(近地飞行)
(1)某星体m围绕中心天体M做圆周运动的周期为T,半径为r
成就二:中心天体密度计算
(2)已知天体M的半径R和表面g
成就一:中心天体质量
三、发现未知天体
探究:英 亚当斯 法 勒维耶
坚信万有引力定律正确,有行星影响
预言了哈雷彗星的回归
问题:天王星的观察轨道为什么与由“万有引力定律”计算出来的理论轨道存在较大的误差?
猜想: 1、“万有引力定律”是错的
2、可能有其它行星的影响而造成的误差
结果:发现了海王星
万有引力定律的应用
测天体的质量、
测天体的密度
发现未知行星,
预测行星、彗星
的运动
思路一:天体表面重力近似等于万有引力
思路二:天体运动中,万有引力提供物体圆周运动向心力
方法归纳:
例1:利用下列哪组数据,可以计算出火星的质量:(已知万有引力恒量)
A、已知火星的半径R和火星表面的重力加速度g
B、已知卫星绕火星做匀速圆周运动的半径r和周期T
C、已知火星绕太阳做匀速圆周运动的半径r和线速度v
D、已知卫星绕火星做匀速圆周运动的线速度v和周期T
【练习】已知引力常量G、地球绕太阳做匀速圆周运动的轨道半径为r,地球绕太阳运行的周期T,仅利用这三个数据,可以估算出的物理量有( )
A.地球的质量
B.太阳的质量
C.太阳的半径
D.地球绕太阳的运行速率
BD
若地球密度为ρ,地球半径为R0,
求地表的重力加速度?
补充:若质量均匀球壳对球壳内的质点引力为零,
则地球内部距离地心为r处的重力加速度多大?
例:假设地球是半径为R,质量分别均匀的球体。
一矿井深度为d。已知质量分布均匀的球壳对球壳
内部的物体的引力为零,则矿井底部和地球表面的
重力加速度之比是
A
B
C
D
理想模型转化:补偿法、切割法、对称法的应用
1、天文观察得某行星线速度为v,离太阳距离r,太阳的半径为R1,行星的半径为R2,则可知太阳质量为 ;太阳的密度为_________
2:从地面上竖直向上发射一航天器,当航天器竖直
向上以加速度a=g/2 匀加速运动时,航天器内物体
对水平支持面的压力为其静止在地球表面时对水平支
持面压力的17/18,已知地球半径为R,求此时航天
器里地面的高度。
3:宇宙中有一星球的质量约为地球质量的9倍,
半径约为地球半径的一半。若从地球上h处水平
抛出一物体,射程是48m,试求:则在该星球上,
从同样高度以同样的初速度水平抛出同一物体,
射程是多少?
思考: 联系天体现象和抛体运动现象的物理量是谁?
重力加速度(引力加速度)
g
6宇航员站在一星球表面上的某高处,沿水平方
向抛出一小球,经过时间t,小球落在星球表面,
测得抛出点与落地点之间的距离为L,若抛出时
的初速度增大到2倍,则抛出点与落地点间的距
离为 L,已知两落地点在同一水平面上,该星球
的半径为R,引力常量为G,
求该星球的质量M和密度ρ.
5、某物体在地面上受到的重力为160 N,将它放
置在卫星中,在卫星以加速度a=g/2 随火箭加速上
升的过程中,当物体与卫星中的支持物的相互压力
为90 N时,求此时卫星距地球表面有多远?
(地球半径R=6.4×103km,g取10m/s2)
【例一】一艘宇宙飞船飞到月球的表面附近,绕月球做近表面匀速圆周运动。若宇航员用一只机械表测得绕得一周所用时间为T,则月球的平均密度是多大?
【例】 地核的体积约为整个地球体积的16%,地核的质量约为地球质量的34%,经估算,地核的平均密度为____(结果取两位有效数字)。(已知地球表面g=9.8m/s2 ,
)
补充:对称、分割、等效方法的应用
例一:若从太阳发出的光射到地面需要约8分20秒,
估算太阳质量的表达式__________,
公式中符号的含义______________________ 。
光速:c=3.0×108m/s
地球公转周期T=365×24×3600=3.15×107s
C光速 T地球公转周期
t光从太阳到地球的时间
水星
Mercury
金星
Venus
地球
Earth
太阳系中密度最大的星体
火星
Mars
木星
Jupiter
土星
Saturn
天王星
Uranus
1781年赫歇尔用望远镜发现了太阳系第七颗行星――天王星以后,科学家经过多年的努力,希望能发现第八颗行星,但是半个多世纪过去了,仍然一无所获。
海王星
Neptune
冥王星
Pluto
海王星、冥王星的发现:
让人们感受到万有引力定律的巨大威力,
彻底消除了人们对牛顿引力学说的怀疑。
当时有两个青年--英国的亚当斯(Adams)和法国的勒威耶(Le Verrier)在互不知晓的情况下分别进行了整整两年的工作。1845年亚当斯先算出结果,但格林尼治天文台却把他的论文束之高阁。1846年9月18日,勒威耶把结果寄到了柏林,却受到了重视。柏林天文台的伽勒(J.G.Galle)于第二天晚上就进行了搜索,并且在离勒威耶预报位置
不远的地方发现了这颗新行星。
海王星的发现使哥白尼学说和
牛顿力学得到了最好的证明。
科学史上的一段佳话
例二:已知地球半径R和月球绕地球的轨道半径r和周期T,则地球的平均密 度表达式为 。
基本
求解
利用
结论
研究 中心天体密度的基本思路(二):
例一:已知地球半径R和地表重力加速度g,则地球的平均密度表达式为 。
不考虑地球自转的影响
利用地表面重力加速度值,计算天体密度
基本
求解
利用
结论
研究 中心天体密度的基本思路(一):
总结:求解天体密度的思路
1.确定情景:环绕现象或地表(无自转)现象
2.建立天体的质量、球体体积公式,求密度
环绕
地面
标
准
解
法
6.4万有引力理论成就
复习:
1、万有引力定律的内容是什么?
2、该定律的适用条件是什么?
3、引力常数G的单位?
万有引力与重力
1、不加说明,万有引力等于重力
2、考虑自转时,重力是万有引力的一个分力
一、天体质量的计算
利用星球表面重力加速度值,计算该星球质量。(不考虑星球自转的影响)
研究天体质量的基本思路(一):
地表处物体m受重力等于万有引力
方法
已知:地球表面的重力加速度是g,地球的半径是R,万有引力常量是G ,请根据这些数据计算地球的质量。
GM=gR2
解:据 地表处物体m受重力等于万有引力:
探究
研究天体质量的基本思路(一):
研究 中心天体质量的基本思路(二):
思路:
已知:匀速圆周运动的周期T和半径R,
求中心天体的质量
物体做匀速圆周运动
万有引力充当向心力
M
V
M为中心天体的质量
结论:
例一: 已知月球绕地球的周期是t,轨道
半径为a;地球绕太阳周期为T,轨道半径为b。
求:地球质量与太阳质量之比
据:
解得中心天体质量
所求比值:
找
通
式
法
A:已知环绕中心天体的行星(卫星)的
轨道半径和角速度。
B:已知环绕中心天体的行星(卫星)的轨道半径r和运行的线速度v。
基本思路:
结论:
求中心天体的质量
思考:
已知天体质量如何求天体密度?
二、天体密度的计算
不考虑地球自转的影响
利用地表面重力加速度g值,计算天体密度
研究 中心天体密度的基本思路(一):
快
速
利
用
结
论
利用绕地球的轨道半径r和周期T,
求地球的平均密 度
研究 中心天体密度的基本思路(二):
快
速
利
用
结
论
讨论:若仅已知一个在地球表面附近运动的
卫星的周期,能否近似求得地球的密度?
总结
(近地飞行)
(1)某星体m围绕中心天体M做圆周运动的周期为T,半径为r
成就二:中心天体密度计算
(2)已知天体M的半径R和表面g
成就一:中心天体质量
三、发现未知天体
探究:英 亚当斯 法 勒维耶
坚信万有引力定律正确,有行星影响
预言了哈雷彗星的回归
问题:天王星的观察轨道为什么与由“万有引力定律”计算出来的理论轨道存在较大的误差?
猜想: 1、“万有引力定律”是错的
2、可能有其它行星的影响而造成的误差
结果:发现了海王星
万有引力定律的应用
测天体的质量、
测天体的密度
发现未知行星,
预测行星、彗星
的运动
思路一:天体表面重力近似等于万有引力
思路二:天体运动中,万有引力提供物体圆周运动向心力
方法归纳:
例1:利用下列哪组数据,可以计算出火星的质量:(已知万有引力恒量)
A、已知火星的半径R和火星表面的重力加速度g
B、已知卫星绕火星做匀速圆周运动的半径r和周期T
C、已知火星绕太阳做匀速圆周运动的半径r和线速度v
D、已知卫星绕火星做匀速圆周运动的线速度v和周期T
【练习】已知引力常量G、地球绕太阳做匀速圆周运动的轨道半径为r,地球绕太阳运行的周期T,仅利用这三个数据,可以估算出的物理量有( )
A.地球的质量
B.太阳的质量
C.太阳的半径
D.地球绕太阳的运行速率
BD
若地球密度为ρ,地球半径为R0,
求地表的重力加速度?
补充:若质量均匀球壳对球壳内的质点引力为零,
则地球内部距离地心为r处的重力加速度多大?
例:假设地球是半径为R,质量分别均匀的球体。
一矿井深度为d。已知质量分布均匀的球壳对球壳
内部的物体的引力为零,则矿井底部和地球表面的
重力加速度之比是
A
B
C
D
理想模型转化:补偿法、切割法、对称法的应用
1、天文观察得某行星线速度为v,离太阳距离r,太阳的半径为R1,行星的半径为R2,则可知太阳质量为 ;太阳的密度为_________
2:从地面上竖直向上发射一航天器,当航天器竖直
向上以加速度a=g/2 匀加速运动时,航天器内物体
对水平支持面的压力为其静止在地球表面时对水平支
持面压力的17/18,已知地球半径为R,求此时航天
器里地面的高度。
3:宇宙中有一星球的质量约为地球质量的9倍,
半径约为地球半径的一半。若从地球上h处水平
抛出一物体,射程是48m,试求:则在该星球上,
从同样高度以同样的初速度水平抛出同一物体,
射程是多少?
思考: 联系天体现象和抛体运动现象的物理量是谁?
重力加速度(引力加速度)
g
6宇航员站在一星球表面上的某高处,沿水平方
向抛出一小球,经过时间t,小球落在星球表面,
测得抛出点与落地点之间的距离为L,若抛出时
的初速度增大到2倍,则抛出点与落地点间的距
离为 L,已知两落地点在同一水平面上,该星球
的半径为R,引力常量为G,
求该星球的质量M和密度ρ.
5、某物体在地面上受到的重力为160 N,将它放
置在卫星中,在卫星以加速度a=g/2 随火箭加速上
升的过程中,当物体与卫星中的支持物的相互压力
为90 N时,求此时卫星距地球表面有多远?
(地球半径R=6.4×103km,g取10m/s2)
【例一】一艘宇宙飞船飞到月球的表面附近,绕月球做近表面匀速圆周运动。若宇航员用一只机械表测得绕得一周所用时间为T,则月球的平均密度是多大?
【例】 地核的体积约为整个地球体积的16%,地核的质量约为地球质量的34%,经估算,地核的平均密度为____(结果取两位有效数字)。(已知地球表面g=9.8m/s2 ,
)
补充:对称、分割、等效方法的应用
例一:若从太阳发出的光射到地面需要约8分20秒,
估算太阳质量的表达式__________,
公式中符号的含义______________________ 。
光速:c=3.0×108m/s
地球公转周期T=365×24×3600=3.15×107s
C光速 T地球公转周期
t光从太阳到地球的时间
水星
Mercury
金星
Venus
地球
Earth
太阳系中密度最大的星体
火星
Mars
木星
Jupiter
土星
Saturn
天王星
Uranus
1781年赫歇尔用望远镜发现了太阳系第七颗行星――天王星以后,科学家经过多年的努力,希望能发现第八颗行星,但是半个多世纪过去了,仍然一无所获。
海王星
Neptune
冥王星
Pluto
海王星、冥王星的发现:
让人们感受到万有引力定律的巨大威力,
彻底消除了人们对牛顿引力学说的怀疑。
当时有两个青年--英国的亚当斯(Adams)和法国的勒威耶(Le Verrier)在互不知晓的情况下分别进行了整整两年的工作。1845年亚当斯先算出结果,但格林尼治天文台却把他的论文束之高阁。1846年9月18日,勒威耶把结果寄到了柏林,却受到了重视。柏林天文台的伽勒(J.G.Galle)于第二天晚上就进行了搜索,并且在离勒威耶预报位置
不远的地方发现了这颗新行星。
海王星的发现使哥白尼学说和
牛顿力学得到了最好的证明。
科学史上的一段佳话
例二:已知地球半径R和月球绕地球的轨道半径r和周期T,则地球的平均密 度表达式为 。
基本
求解
利用
结论
研究 中心天体密度的基本思路(二):
例一:已知地球半径R和地表重力加速度g,则地球的平均密度表达式为 。
不考虑地球自转的影响
利用地表面重力加速度值,计算天体密度
基本
求解
利用
结论
研究 中心天体密度的基本思路(一):
总结:求解天体密度的思路
1.确定情景:环绕现象或地表(无自转)现象
2.建立天体的质量、球体体积公式,求密度
环绕
地面
标
准
解
法
