人教版高中数学必修四 1.3三角函数的诱导公式(共130张PPT)
文档属性
| 名称 | 人教版高中数学必修四 1.3三角函数的诱导公式(共130张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-11 00:00:00 | ||
图片预览








文档简介
(共130张PPT)
1.3 三角函数的诱导公式(1)
第一章 三角函数
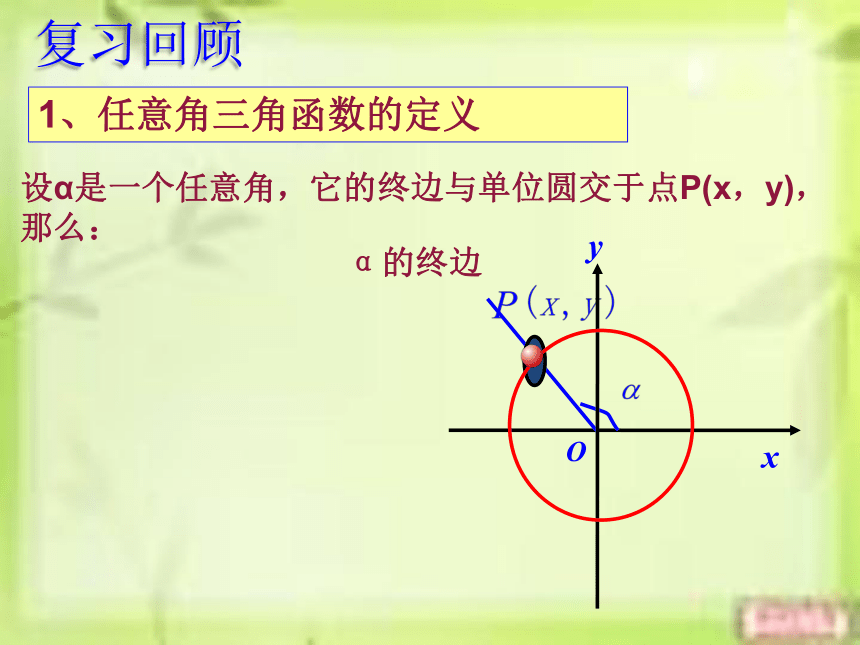
1、任意角三角函数的定义
复习回顾
1、任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
y
O
x
α的终边
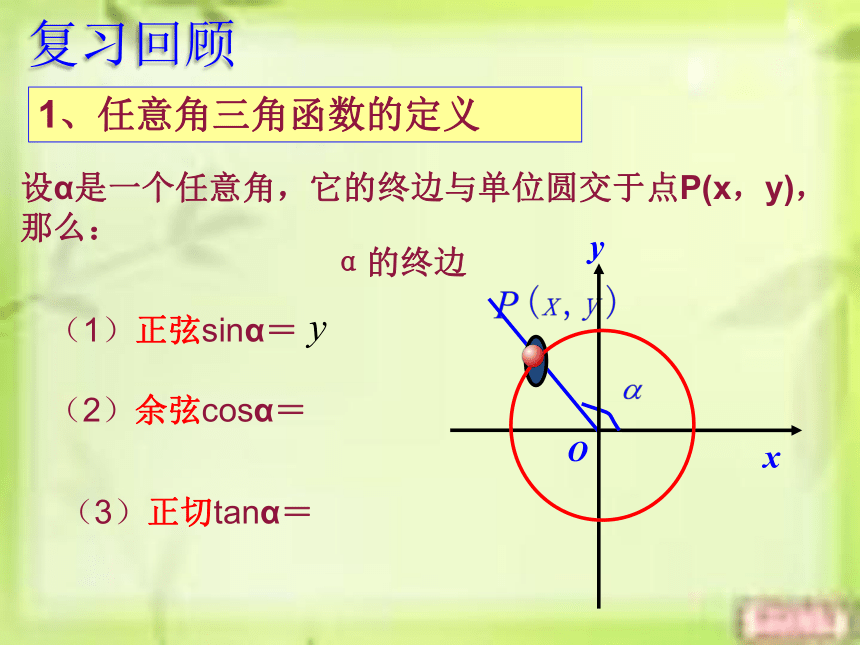
复习回顾
1、任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
y
O
x
α的终边
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
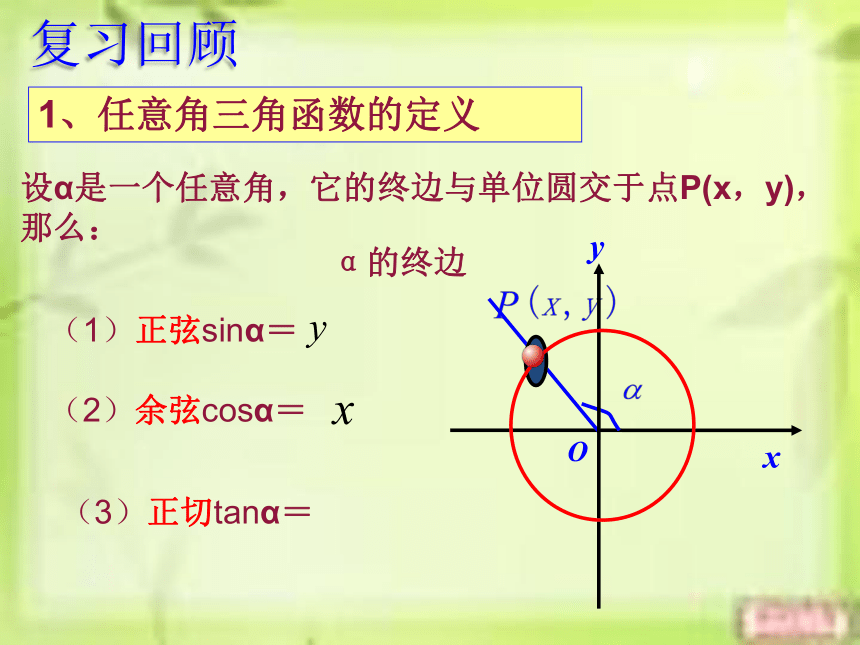
复习回顾
1、任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
y
O
x
α的终边
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
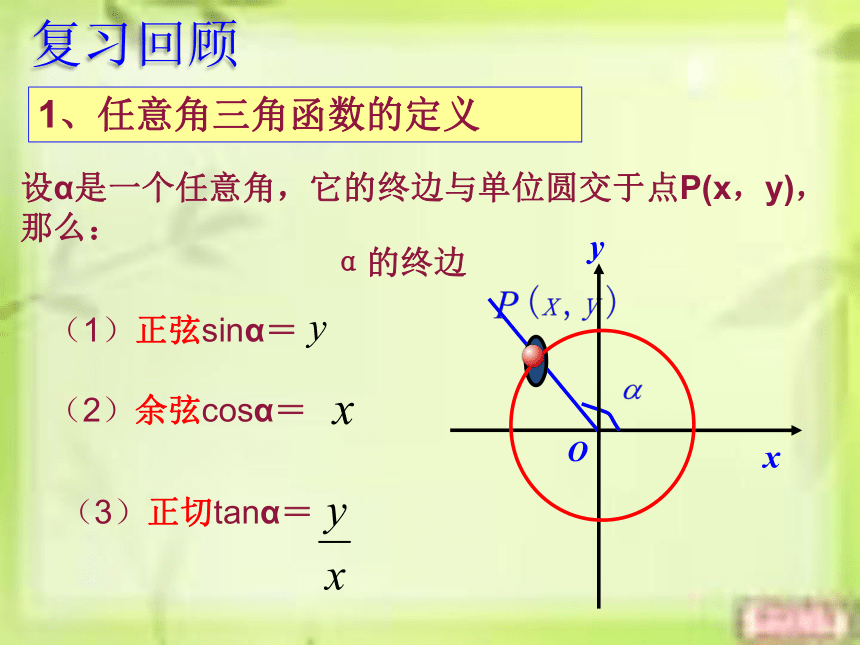
复习回顾
1、任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
y
O
x
α的终边
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
复习回顾
1、任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
y
O
x
α的终边
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
复习回顾
2、诱导公式(一)
复习回顾
2、诱导公式(一)
复习回顾
2、诱导公式(一)
复习回顾
1)实质:终边相同的角的同一三角函数值相等
2、诱导公式(一)
复习回顾
1)实质:终边相同角的同一三角函数值相等
2)用途:把求任意角的三角函数值,化为00~3600角的三角函数值来求.即“大”角化“小”角
2、诱导公式(一)
复习回顾
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
思考
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
思考
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
我们能求出锐角的三角函数值,若能把求非锐角三角函数值,转化为求有关锐角α的三角函数值,则这个问题将得以解决.
试一试
你能求sin750°和sin930°的值吗?
新课引入
我们能求出锐角的三角函数值,若能把求非锐角三角函数值,转化为求有关锐角α的三角函数值,则这个提到的问题将得以解决.
试一试
这一思想就是数学中的化归思想.
24
本节课的目的就是如何把求任意角的三角函数值问题转化为 的三角函数值问题
25
本节课的目的就是如何把求任意角的三角函数值问题转化为 的三角函数值问题
26
本节课的目的就是如何把求任意角的三角函数值问题转化为 的三角函数值问题
下面我们就先探究1800+?与?的三角函数值的关系
公式的推导
探究1、1800+?与?的三角函数值的关系
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
圆具有很好的对称性
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
(2)
角
与角
的终边与单位圆的交点P,P1
之间有怎样的对称关系?
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
关于原点对称。
(2)
角
与角
的终边与单位圆的交点P,P1
之间有怎样的对称关系?
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
关于原点对称。
(3)
P与P1的坐标有怎样的关系?
(2)
角
与角
的终边与单位圆的交点P,P1
之间有怎样的对称关系?
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
关于原点对称。
(3)
P与P1的坐标有怎样的关系?
(2)
角
与角
的终边与单位圆的交点P,P1
之间有怎样的对称关系?
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
关于原点对称。
(3)
P与P1的坐标有怎样的关系?
(2)
角
与角
的终边与单位圆的交点P,P1
之间有怎样的对称关系?
P与P1
横坐标互为相反数,
P与P1的
思考
纵坐标互为相反数。
公式的推导
思考
公式的推导
思考
公式的推导
可得出结论:无论α是锐角还是任意角,1800+?的终边都是α角的终边的反向延长线,它们与单位圆的交点P,P1关于原点对称横坐标互为相反数,终坐标互为相反数,
思考
π+α的三角函数值与α的三角函数值之间的关系
P(x, y)
P'(-x, -y)
归纳
π+α的三角函数值与α的三角函数值之间的关系
P(x, y)
P'(-x, -y)
归纳
π+α的三角函数值与α的三角函数值之间的关系
P(x, y)
P'(-x, -y)
公式二
归纳
公式二有何作用?
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
想一想
公式二
公式二有何作用?
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
将第三象限角的三角函数转化为第一象限角的三角函数。
想一想
公式二
公式二有何作用?
例如:sin 210°=
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
将第三象限角的三角函数转化为第一象限角的三角函数。
想一想
?
tan 210°=
公式二
公式二有何作用?
例如:sin 210°=.sin(180°+30°)=-sin 30°=
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
将第三象限角的三角函数转化为第一象限角的三角函数。
想一想
?
tan 210°=
公式二
公式二有何作用?
例如:sin 210°=.sin(180°+30°)=-sin 30°=
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
将第三象限角的三角函数转化为第一象限角的三角函数。
想一想
?
?
?
?
tan 210°=
公式二
公式二有何作用?
例如:sin 210°=.sin(180°+30°)=-sin 30°=
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
将第三象限角的三角函数转化为第一象限角的三角函数。
想一想
?
?
?
?
tan 210°=
公式二
1)-?的终边与角α的终边有什么关系?
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
1)-?的终边与角α的终边有什么关系?
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
1)-?的终边与角α的终边有什么关系?
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
-α
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
1)-?的终边与角α的终边有什么关系? 关于x轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
-α
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
1)-?的终边与角α的终边有什么关系? 关于x轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
-α
P'(x, -y)
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
1)-?的终边与角α的终边有什么关系? 关于x轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
横坐标相等,终坐标互为相反数。
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
-α
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
P'(x, -y)
1)-?的终边与角α的终边有什么关系? 关于x轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
横坐标相等,终坐标互为相反数。
3)它们的三角函数之间有什么关系?
公式三
y
α
x
O
P(x,y)
-α
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
P'(x, -y)
诱导公式三有何作用?
想一想
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
诱导公式三有何作用?
想一想
将负角的三角函数转化为正角的三角函数.
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
诱导公式三有何作用?
想一想
将负角的三角函数转化为正角的三角函数.
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
sin(-390°)°
例如
诱导公式三有何作用?
想一想
将负角的三角函数转化为正角的三角函数.
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
sin(-390°)°
例如
诱导公式三有何作用?
想一想
将负角的三角函数转化为正角的三角函数.
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
sin(-390°)=-sin390°=-sin30°
例如
诱导公式三有何作用?
想一想
将负角的三角函数转化为正角的三角函数.
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
sin(-390°)=-sin390°=-sin30°
例如
=-1
将下列三角函数转化为锐角三角函数,并填在题中横线上
练习
1、将下列三角函数转化为锐角三角函数,并填在题中横线上
练习
1、将下列三角函数转化为锐角三角函数,并填在题中横线上
练习
1、将下列三角函数转化为锐角三角函数,并填在题中横线上
练习
1、将下列三角函数转化为锐角三角函数,并填在题中横线上
练习
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系?
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
y
α
x
O
P(x,y)
α
π-α
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系?
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
α
π-α
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系? 关于y轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
α
π-α
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系? 关于y轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
P'(-x, y)
y
α
x
O
P(x,y)
α
π-α
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系? 关于y轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
横坐标互为相反数,终坐标相等。
3)它们的三角函数之间有什么关系?
P'(-x, y)
公式四
y
α
x
O
P(x,y)
α
π-α
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系? 关于x轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
横坐标互为相反数,终坐标相等。
3)它们的三角函数之间有什么关系?
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
P'(-x, y)
公式四还可以根据公式一和公式三推导如下
sin(π-α)=sin = - sin(-α)=
sinα
cos(π-α)=cos = - cos(-α)= -
cosα
tan(π-α)= tan =tan(-α)=-tanα
sin(π-α) = sinα
cos(π-α) =-cosα
tan(π-α) =-tanα
公式四
想一想
诱导公式四有何作用?
将第二象限角的三角函数转化为第一象限角的三角函数.
sin(π-α) = sinα
cos(π-α) =-cosα
tan(π-α) =-tanα
公式四
想一想
诱导公式四有何作用?
将第二象限角的三角函数转化为第一象限角的三角函数.
sin(π-α) = sinα
cos(π-α) =-cosα
tan(π-α) =-tanα
公式四
想一想
诱导公式四有何作用?
将第二象限角的三角函数转化为第一象限角的三角函数.
sin(π-α) = sinα
cos(π-α) =-cosα
tan(π-α) =-tanα
公式四
想一想
诱导公式四有何作用?
公式一:
公式二:
公式三:
公式四:
公式一:
公式二:
公式三:
公式四:
公式一~四都叫做诱导公式,他们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数与α的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗?
公式一:
公式二:
公式三:
公式四:
概括如下:2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,前面加上一个把看成锐角时原函数值的符号
公式一~四都叫做诱导公式,他们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数与α的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗?
公式一:
公式二:
公式三:
公式四:
概括如下:2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,前面加上一个把看成锐角时原函数值的符号
公式一~四都叫做诱导公式,他们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数与α的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗?
“函数名不变,符号看象限”.
公式一:
公式二:
公式三:
公式四:
注意
1、公式中的角α可以是任意角,只是因为公式记忆的方便,把α看成锐角
记忆口诀
“函数名不变,符号看象限”
2、诱导公式都是恒等式,即在等式有意义时恒成立.
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
另解
(4)cos(-2 040°).
(4)cos(-2 040°).
解 cos(-2 040°)=cos 2 040°
=cos(6×360°-120°)
=cos 120°=cos(180°-60°)
=-cos 60°=-.
(4)cos(-2 040°).
=cos(-2 040°)=cos(-6×360°+120°)=cos120°=.
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
(1)化负角的三角函数为正角的三角函数。
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
(1)化负角的三角函数为正角的三角函数。
(2)化为
~
的三角函数。
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
(1)化负角的三角函数为正角的三角函数。
(2)化为
~
的三角函数。
(3)化为锐角的三角函数。
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
(1)化负角的三角函数为正角的三角函数。
(2)化为
~
的三角函数。
(3)化为锐角的三角函数。
概括为:“负化正,正化小,化到锐角就成了。”
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
(1)化负角的三角函数为正角的三角函数。
(2)化为
~
的三角函数。
(3)化为锐角的三角函数。
概括为:“负化正,正化小,化到锐角就终了。”
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
上述过程体现了由未知到已知的化归思想。
利用诱导公式把任意角的三角函数转化为锐角函数的一般步骤:
任意负角的
三角函数
任意正角的
三角函数
锐角三
角函数
0~2π的角的三角函数
用框图表示为:
利用诱导公式把任意角的三角函数转化为锐角函数的一般步骤:
任意负角的
三角函数
任意正角的
三角函数
用公式
三或一
锐角三
角函数
用公式
二或四
0~2π的角的三角函数
用公式一
用框图表示为:
利用公式求下列三角函数值:
练习
(1)cos(-420°).
(2)sin( ).
(3)sin(-1500°).
(4)cos( ).
利用公式求下列三角函数值:
练习
(1)cos(-420°).
(2)sin( ).
(3)sin(-1500°).
(4)cos( ).
例2.化简:
公式的应用
113
解:
例2.化简:
公式的应用
114
解:
例2.化简:
公式的应用
115
所以原式
解:
例2.化简:
公式的应用
化简
练习
化简
练习
例3
公式的应用
挖掘角的相互关系,寻求诱导公式的应用
例3
公式的应用
互补关系
挖掘角的相互关系,寻求诱导公式的应用
例3
公式的应用
例3
解
练习
4. 已知角?的终边上的一点P(3a,4a) (a<0)
则cos(5400-?)的值是 。
5、求 的值(n?Z)
6、将sin 转化为锐角三角函数()
A.sin2
B.-sin2
C.sin
D.-sin
思考
是否正确?
因为
因为
所以
以诱导公式一~四为基础,还可以产生一些派生公式
填写下表并熟记
本节课学了哪些知识?
能解决哪些问题?
涉及到哪些数学思想方法?
课堂小结
1.知识点:诱导公式二~四
2.数学思想方法:
转化与化归思想,数形结合思想;
3.题型:求值、化简
课堂小结
(1)诱导公式的推导与形式;结合图形(对称性)
(2)记忆口诀“函数名不变,符号看象限”
(3)诱导公式的简单应用.
作业:P29,
A组
1t;填书上
2t.(1)(6); 3t
选作:B组 1t
关注“掌上平遥APP”下载课后习题
1.3 三角函数的诱导公式(1)
第一章 三角函数
1、任意角三角函数的定义
复习回顾
1、任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
y
O
x
α的终边
复习回顾
1、任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
y
O
x
α的终边
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
复习回顾
1、任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
y
O
x
α的终边
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
复习回顾
1、任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
y
O
x
α的终边
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
复习回顾
1、任意角三角函数的定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
y
O
x
α的终边
(1)正弦sinα=
(2)余弦cosα=
(3)正切tanα=
复习回顾
2、诱导公式(一)
复习回顾
2、诱导公式(一)
复习回顾
2、诱导公式(一)
复习回顾
1)实质:终边相同的角的同一三角函数值相等
2、诱导公式(一)
复习回顾
1)实质:终边相同角的同一三角函数值相等
2)用途:把求任意角的三角函数值,化为00~3600角的三角函数值来求.即“大”角化“小”角
2、诱导公式(一)
复习回顾
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
思考
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
思考
你能求sin750°和sin930°的值吗?
新课引入
试一试
你能求sin750°和sin930°的值吗?
新课引入
我们能求出锐角的三角函数值,若能把求非锐角三角函数值,转化为求有关锐角α的三角函数值,则这个问题将得以解决.
试一试
你能求sin750°和sin930°的值吗?
新课引入
我们能求出锐角的三角函数值,若能把求非锐角三角函数值,转化为求有关锐角α的三角函数值,则这个提到的问题将得以解决.
试一试
这一思想就是数学中的化归思想.
24
本节课的目的就是如何把求任意角的三角函数值问题转化为 的三角函数值问题
25
本节课的目的就是如何把求任意角的三角函数值问题转化为 的三角函数值问题
26
本节课的目的就是如何把求任意角的三角函数值问题转化为 的三角函数值问题
下面我们就先探究1800+?与?的三角函数值的关系
公式的推导
探究1、1800+?与?的三角函数值的关系
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
圆具有很好的对称性
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
(2)
角
与角
的终边与单位圆的交点P,P1
之间有怎样的对称关系?
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
关于原点对称。
(2)
角
与角
的终边与单位圆的交点P,P1
之间有怎样的对称关系?
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
关于原点对称。
(3)
P与P1的坐标有怎样的关系?
(2)
角
与角
的终边与单位圆的交点P,P1
之间有怎样的对称关系?
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
关于原点对称。
(3)
P与P1的坐标有怎样的关系?
(2)
角
与角
的终边与单位圆的交点P,P1
之间有怎样的对称关系?
思考
公式的推导
探究1、1800+?与?的三角函数值的关系
关于原点对称。
关于原点对称。
(3)
P与P1的坐标有怎样的关系?
(2)
角
与角
的终边与单位圆的交点P,P1
之间有怎样的对称关系?
P与P1
横坐标互为相反数,
P与P1的
思考
纵坐标互为相反数。
公式的推导
思考
公式的推导
思考
公式的推导
可得出结论:无论α是锐角还是任意角,1800+?的终边都是α角的终边的反向延长线,它们与单位圆的交点P,P1关于原点对称横坐标互为相反数,终坐标互为相反数,
思考
π+α的三角函数值与α的三角函数值之间的关系
P(x, y)
P'(-x, -y)
归纳
π+α的三角函数值与α的三角函数值之间的关系
P(x, y)
P'(-x, -y)
归纳
π+α的三角函数值与α的三角函数值之间的关系
P(x, y)
P'(-x, -y)
公式二
归纳
公式二有何作用?
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
想一想
公式二
公式二有何作用?
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
将第三象限角的三角函数转化为第一象限角的三角函数。
想一想
公式二
公式二有何作用?
例如:sin 210°=
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
将第三象限角的三角函数转化为第一象限角的三角函数。
想一想
?
tan 210°=
公式二
公式二有何作用?
例如:sin 210°=.sin(180°+30°)=-sin 30°=
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
将第三象限角的三角函数转化为第一象限角的三角函数。
想一想
?
tan 210°=
公式二
公式二有何作用?
例如:sin 210°=.sin(180°+30°)=-sin 30°=
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
将第三象限角的三角函数转化为第一象限角的三角函数。
想一想
?
?
?
?
tan 210°=
公式二
公式二有何作用?
例如:sin 210°=.sin(180°+30°)=-sin 30°=
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
将第三象限角的三角函数转化为第一象限角的三角函数。
想一想
?
?
?
?
tan 210°=
公式二
1)-?的终边与角α的终边有什么关系?
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
1)-?的终边与角α的终边有什么关系?
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
1)-?的终边与角α的终边有什么关系?
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
-α
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
1)-?的终边与角α的终边有什么关系? 关于x轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
-α
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
1)-?的终边与角α的终边有什么关系? 关于x轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
-α
P'(x, -y)
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
1)-?的终边与角α的终边有什么关系? 关于x轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
横坐标相等,终坐标互为相反数。
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
-α
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
P'(x, -y)
1)-?的终边与角α的终边有什么关系? 关于x轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
横坐标相等,终坐标互为相反数。
3)它们的三角函数之间有什么关系?
公式三
y
α
x
O
P(x,y)
-α
公式的推导
探究2、-?与?的三角函数值的关系
对于任意给定的一个角α
思考
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
P'(x, -y)
诱导公式三有何作用?
想一想
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
诱导公式三有何作用?
想一想
将负角的三角函数转化为正角的三角函数.
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
诱导公式三有何作用?
想一想
将负角的三角函数转化为正角的三角函数.
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
sin(-390°)°
例如
诱导公式三有何作用?
想一想
将负角的三角函数转化为正角的三角函数.
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
sin(-390°)°
例如
诱导公式三有何作用?
想一想
将负角的三角函数转化为正角的三角函数.
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
sin(-390°)=-sin390°=-sin30°
例如
诱导公式三有何作用?
想一想
将负角的三角函数转化为正角的三角函数.
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
sin(-390°)=-sin390°=-sin30°
例如
=-1
将下列三角函数转化为锐角三角函数,并填在题中横线上
练习
1、将下列三角函数转化为锐角三角函数,并填在题中横线上
练习
1、将下列三角函数转化为锐角三角函数,并填在题中横线上
练习
1、将下列三角函数转化为锐角三角函数,并填在题中横线上
练习
1、将下列三角函数转化为锐角三角函数,并填在题中横线上
练习
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系?
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
y
α
x
O
P(x,y)
α
π-α
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系?
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
α
π-α
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系? 关于y轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
y
α
x
O
P(x,y)
α
π-α
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系? 关于y轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
3)它们的三角函数之间有什么关系?
P'(-x, y)
y
α
x
O
P(x,y)
α
π-α
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系? 关于y轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
横坐标互为相反数,终坐标相等。
3)它们的三角函数之间有什么关系?
P'(-x, y)
公式四
y
α
x
O
P(x,y)
α
π-α
公式的推导
探究3、π-?与?的三角函数值的关系
思考
对于任意给定的一个角α
1)-?的终边与角α的终边有什么关系? 关于x轴对称
2)它们的终边与单位圆的交点坐标有什么关系?
横坐标互为相反数,终坐标相等。
3)它们的三角函数之间有什么关系?
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
P'(-x, y)
公式四还可以根据公式一和公式三推导如下
sin(π-α)=sin = - sin(-α)=
sinα
cos(π-α)=cos = - cos(-α)= -
cosα
tan(π-α)= tan =tan(-α)=-tanα
sin(π-α) = sinα
cos(π-α) =-cosα
tan(π-α) =-tanα
公式四
想一想
诱导公式四有何作用?
将第二象限角的三角函数转化为第一象限角的三角函数.
sin(π-α) = sinα
cos(π-α) =-cosα
tan(π-α) =-tanα
公式四
想一想
诱导公式四有何作用?
将第二象限角的三角函数转化为第一象限角的三角函数.
sin(π-α) = sinα
cos(π-α) =-cosα
tan(π-α) =-tanα
公式四
想一想
诱导公式四有何作用?
将第二象限角的三角函数转化为第一象限角的三角函数.
sin(π-α) = sinα
cos(π-α) =-cosα
tan(π-α) =-tanα
公式四
想一想
诱导公式四有何作用?
公式一:
公式二:
公式三:
公式四:
公式一:
公式二:
公式三:
公式四:
公式一~四都叫做诱导公式,他们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数与α的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗?
公式一:
公式二:
公式三:
公式四:
概括如下:2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,前面加上一个把看成锐角时原函数值的符号
公式一~四都叫做诱导公式,他们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数与α的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗?
公式一:
公式二:
公式三:
公式四:
概括如下:2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,前面加上一个把看成锐角时原函数值的符号
公式一~四都叫做诱导公式,他们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数与α的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗?
“函数名不变,符号看象限”.
公式一:
公式二:
公式三:
公式四:
注意
1、公式中的角α可以是任意角,只是因为公式记忆的方便,把α看成锐角
记忆口诀
“函数名不变,符号看象限”
2、诱导公式都是恒等式,即在等式有意义时恒成立.
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
二、探 究
例1.利用公式求下列三角函数值:
公式的应用
解 (1)cos 225°=cos(180°+45°)
另解
(4)cos(-2 040°).
(4)cos(-2 040°).
解 cos(-2 040°)=cos 2 040°
=cos(6×360°-120°)
=cos 120°=cos(180°-60°)
=-cos 60°=-.
(4)cos(-2 040°).
=cos(-2 040°)=cos(-6×360°+120°)=cos120°=.
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
(1)化负角的三角函数为正角的三角函数。
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
(1)化负角的三角函数为正角的三角函数。
(2)化为
~
的三角函数。
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
(1)化负角的三角函数为正角的三角函数。
(2)化为
~
的三角函数。
(3)化为锐角的三角函数。
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
(1)化负角的三角函数为正角的三角函数。
(2)化为
~
的三角函数。
(3)化为锐角的三角函数。
概括为:“负化正,正化小,化到锐角就成了。”
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
(1)化负角的三角函数为正角的三角函数。
(2)化为
~
的三角函数。
(3)化为锐角的三角函数。
概括为:“负化正,正化小,化到锐角就终了。”
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
反思与感悟
上述过程体现了由未知到已知的化归思想。
利用诱导公式把任意角的三角函数转化为锐角函数的一般步骤:
任意负角的
三角函数
任意正角的
三角函数
锐角三
角函数
0~2π的角的三角函数
用框图表示为:
利用诱导公式把任意角的三角函数转化为锐角函数的一般步骤:
任意负角的
三角函数
任意正角的
三角函数
用公式
三或一
锐角三
角函数
用公式
二或四
0~2π的角的三角函数
用公式一
用框图表示为:
利用公式求下列三角函数值:
练习
(1)cos(-420°).
(2)sin( ).
(3)sin(-1500°).
(4)cos( ).
利用公式求下列三角函数值:
练习
(1)cos(-420°).
(2)sin( ).
(3)sin(-1500°).
(4)cos( ).
例2.化简:
公式的应用
113
解:
例2.化简:
公式的应用
114
解:
例2.化简:
公式的应用
115
所以原式
解:
例2.化简:
公式的应用
化简
练习
化简
练习
例3
公式的应用
挖掘角的相互关系,寻求诱导公式的应用
例3
公式的应用
互补关系
挖掘角的相互关系,寻求诱导公式的应用
例3
公式的应用
例3
解
练习
4. 已知角?的终边上的一点P(3a,4a) (a<0)
则cos(5400-?)的值是 。
5、求 的值(n?Z)
6、将sin 转化为锐角三角函数()
A.sin2
B.-sin2
C.sin
D.-sin
思考
是否正确?
因为
因为
所以
以诱导公式一~四为基础,还可以产生一些派生公式
填写下表并熟记
本节课学了哪些知识?
能解决哪些问题?
涉及到哪些数学思想方法?
课堂小结
1.知识点:诱导公式二~四
2.数学思想方法:
转化与化归思想,数形结合思想;
3.题型:求值、化简
课堂小结
(1)诱导公式的推导与形式;结合图形(对称性)
(2)记忆口诀“函数名不变,符号看象限”
(3)诱导公式的简单应用.
作业:P29,
A组
1t;填书上
2t.(1)(6); 3t
选作:B组 1t
关注“掌上平遥APP”下载课后习题
