3.2.1古典概型的特征和概率计算公式(共25张PPT)
文档属性
| 名称 | 3.2.1古典概型的特征和概率计算公式(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 22:34:45 | ||
图片预览






文档简介
(共25张PPT)
3.2.1 古典概型的特征和概率计算公式
第三章:概率
问题提出
甲乙两个赌徒打赌:同时掷两颗骰子,以两颗骰子的点数和打赌,甲压3点,乙压7点,谁赢的机会比较大?
课堂训练
课堂小结
典型例题
方法探究
基本概念
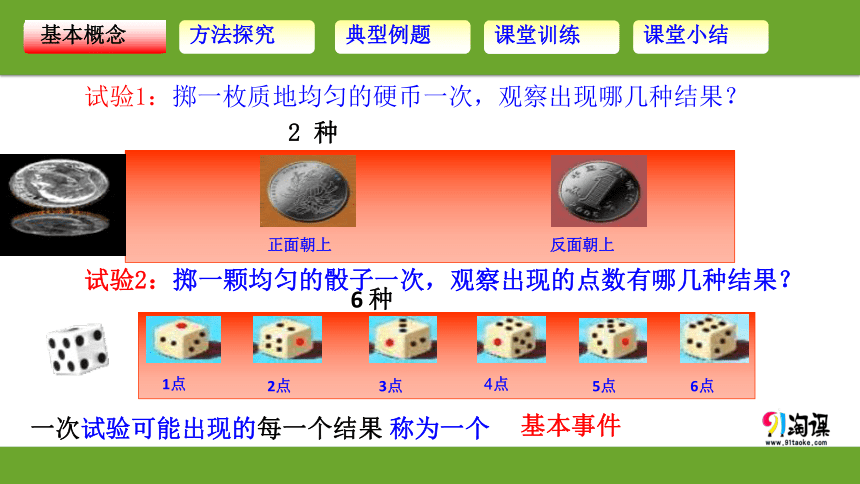
试验2:掷一颗均匀的骰子一次,观察出现的点数有哪几种结果?
试验1:掷一枚质地均匀的硬币一次,观察出现哪几种结果?
2 种
正面朝上
反面朝上
6 种
4点
1点
2点
3点
5点
6点
一次试验可能出现的每一个结果 称为一个
基本事件
课堂训练
课堂小结
典型例题
方法探究
基本概念
课堂训练
课堂小结
典型例题
方法探究
基本概念
例1 从字母a、b、c、d任意取出两个不同字母的试验中,有哪些基本事件?
解:所求的基本事件共有6个:
a
b
c
d
b
c
d
c
d
树状图
课堂训练
课堂小结
典型例题
方法探究
基本概念
六个基本事件
的概率都是
“1点”、“2点”
“3点”、“4点”
“5点”、“6点”
“正面朝上”
“反面朝上”
基本事件
试验2
试验1
基本事件出现的可能性
两个基本事件
的概率都是
问题2:观察对比,找出试验1和试验2的共同特点:
(1)
试验中所有可能出现的基本事件的个数
只有有限个
相等
(2)
每个基本事件出现的可能性
等可能性
(1)
试验中所有可能出现的基本事件的个数
(2)
每个基本事件出现的可能性
相等
只有有限个
我们将具有这两个特点的概率模型称为
古典概率模型
古典概型
简称:
课堂训练
课堂小结
典型例题
方法探究
基本概念
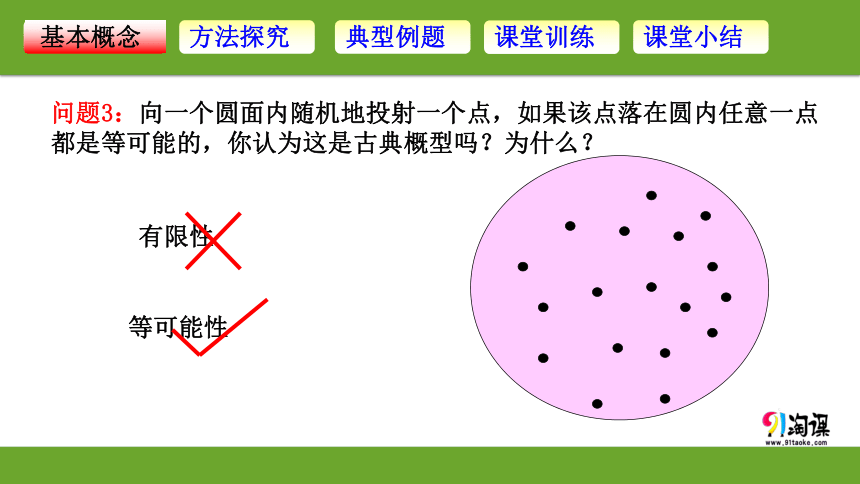
有限性
等可能性
问题3:向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么?
有限性
等可能性
课堂训练
课堂小结
典型例题
方法探究
基本概念
问题4:”向上抛掷一枚不均匀的旧硬币”你认为这是古典概型吗?
为什么?
有限性
等可能性
课堂训练
课堂小结
典型例题
方法探究
基本概念
实验1中,出现正面朝上的概率与反面朝上的概率相等,即
P(“正面朝上”)=P(“反面朝上”)
由概率的加法公式,得
P(“正面朝上”)+P(“反面朝上”)=P(必然事件)=1
因此 P(“正面朝上”)=P(“反面朝上”)=
即
问题5:
在古典概率模型中,如何求随机事件出现的概率?
掷一颗均匀的骰子,
试验2:
为“出现偶数点”,请问事件 A的概率是多少?
事件A
探讨:
事件A 包含 个基本事件:
2点 4点 6点
3
P(A)
(“4点”)
P
P(“2点”)
(“6点”)
P
方法探究
课堂训练
课堂小结
典型例题
基本概念
基本事件总数为:
6
?
1点,2点,3点,4点,5点,6点
P(“出现偶数点”)=
方法探究
课堂训练
课堂小结
典型例题
基本概念
古典概型的概率计算公式:
(1)要判断所用概率模型是不是古典概型(前提)
在使用古典概型的概率公式时,应该注意:
P(A)=
(2)要找出随机事件A包含的基本事件的个数和试验中基本
事件的总数。
例2 先后抛掷两枚均匀的硬币,会出现几种结果?列举出来.
出现“一枚正面向上,一枚反面向上”的概率是多少?
解:基本事件有:
( 正 ,正 )( 正 ,反 )
( 反,正 )( 反 ,反)
P(A)=
典型例题
课堂训练
课堂小结
方法探究
基本概念
设A={一枚正面向上,一枚反面向上}
例3 先后掷两个均匀的骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是7的结果有多少种?
(3)向上的点数之和是7的概率是多少?
解:(1)掷一个骰子的结果有6种,我们把两个骰子标上记号1,2以便区分,它总共出现的情况如下表所示:
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
从表中可以看出同时掷两个骰子的结果共有36种。
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子 2号骰子
典型例题
课堂训练
课堂小结
方法探究
基本概念
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子 2号骰子
(2)在上面的结果中,向上的点数之和为7的结果有6种,分别为:
(3)由于所有36种结果是等可能的,其中向上点数之和为7的结果(记为事件A)有6种,因此,
(6,1),(5,2),(4,3),(3,4)(1,6),(2,5)
=
P(A)=
=
(6, 1)
(5, 2)
(4, 3)
(3, 4)
(2, 5)
(1, 6)
典型例题
课堂训练
课堂小结
方法探究
基本概念
为什么要把两个骰子标上记号?如果不标记号会出现什么情况?你能解释其中的原因吗?
如果不标上记号,类似于(3,6)和(6,3)的结果将没有区别。这时,所有可能的结果将是:
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子 2号骰子
(3,6)
(4,5)
因此,在投掷两个骰子的过程中,我们必须对两个骰子加以标号区分
(3,6)
(3,3)
概率不相等
?
概率相等吗?
课堂小结
典型例题
课堂训练
方法探究
2.
从1,2,3,4,5,6,7,8,9这九个自然数中任选一个,
所选中的数是3
的倍数的概率为
基本概念
3.
一副扑克牌,去掉大王和小王,在剩下的52张牌中随意抽出一张牌,
试求以下各个事件的概率:
A:
抽到一张Q
B:
抽到一张“梅花”
C:
抽到一张红桃 K
1.
单选题是标准化考试中常用的题型,一般是从A,B,C ,D
四个
选项中选择一个正确的答案。
假设考生不会做,他随机地选择了一个答案,则他
答对的概率为
1.
单选题是标准化考试中常用的题型,一般是从A,B,C,D
四个
选项中选择一个正确的答案。
假设考生不会做,他随机地选择了一个答案,则他答对的概率
为
课堂小结
典型例题
课堂训练
方法探究
基本概念
基本事件总共有几个?
“答对”包含几个基本事件?
4个:A,B,C,D
1个
课堂小结
典型例题
课堂训练
方法探究
2.
从
1,2,3,4,5,6,7,8,9
这九个自然数中任选一个,
所选中的数是3
的倍数的概率为
基本概念
3.
一副扑克牌,去掉大王和小王,在剩下的52张牌中随意抽出
一张牌,
试求以下各个事件的概率:
A:
抽到一张Q
B:
抽到一张“梅花”
C:
抽到一张红桃 K
2、练习1中如果该题是不定项选择题,假如考生也不会做,则他能够答对的
概率为多少?
此时比单选题容易了,还是更难了?
1、同时抛掷三枚均匀的硬币,会出现几种结果?
出现 “一枚正面向上,两枚反面向上”的概率是多少?
机动
练习
有限个
可能性
古典概型
基本事件
可能结果
基本事件数
课堂训练
典型例题
方法探究
基本概念
列举法(树状图或列表),应做到不重不漏。
(2)古典概型的定义和特点
(3)古典概型计算任何事件A的概率计算公式
(1)基本事件的两个特点:
1.知识点:
2. 基本事件计算的常用方法:
课堂小结
http://www.91taoke.com
谢谢观看!
第三章:概率
3.2.1 古典概型的特征和概率计算公式
第三章:概率
问题提出
甲乙两个赌徒打赌:同时掷两颗骰子,以两颗骰子的点数和打赌,甲压3点,乙压7点,谁赢的机会比较大?
课堂训练
课堂小结
典型例题
方法探究
基本概念
试验2:掷一颗均匀的骰子一次,观察出现的点数有哪几种结果?
试验1:掷一枚质地均匀的硬币一次,观察出现哪几种结果?
2 种
正面朝上
反面朝上
6 种
4点
1点
2点
3点
5点
6点
一次试验可能出现的每一个结果 称为一个
基本事件
课堂训练
课堂小结
典型例题
方法探究
基本概念
课堂训练
课堂小结
典型例题
方法探究
基本概念
例1 从字母a、b、c、d任意取出两个不同字母的试验中,有哪些基本事件?
解:所求的基本事件共有6个:
a
b
c
d
b
c
d
c
d
树状图
课堂训练
课堂小结
典型例题
方法探究
基本概念
六个基本事件
的概率都是
“1点”、“2点”
“3点”、“4点”
“5点”、“6点”
“正面朝上”
“反面朝上”
基本事件
试验2
试验1
基本事件出现的可能性
两个基本事件
的概率都是
问题2:观察对比,找出试验1和试验2的共同特点:
(1)
试验中所有可能出现的基本事件的个数
只有有限个
相等
(2)
每个基本事件出现的可能性
等可能性
(1)
试验中所有可能出现的基本事件的个数
(2)
每个基本事件出现的可能性
相等
只有有限个
我们将具有这两个特点的概率模型称为
古典概率模型
古典概型
简称:
课堂训练
课堂小结
典型例题
方法探究
基本概念
有限性
等可能性
问题3:向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么?
有限性
等可能性
课堂训练
课堂小结
典型例题
方法探究
基本概念
问题4:”向上抛掷一枚不均匀的旧硬币”你认为这是古典概型吗?
为什么?
有限性
等可能性
课堂训练
课堂小结
典型例题
方法探究
基本概念
实验1中,出现正面朝上的概率与反面朝上的概率相等,即
P(“正面朝上”)=P(“反面朝上”)
由概率的加法公式,得
P(“正面朝上”)+P(“反面朝上”)=P(必然事件)=1
因此 P(“正面朝上”)=P(“反面朝上”)=
即
问题5:
在古典概率模型中,如何求随机事件出现的概率?
掷一颗均匀的骰子,
试验2:
为“出现偶数点”,请问事件 A的概率是多少?
事件A
探讨:
事件A 包含 个基本事件:
2点 4点 6点
3
P(A)
(“4点”)
P
P(“2点”)
(“6点”)
P
方法探究
课堂训练
课堂小结
典型例题
基本概念
基本事件总数为:
6
?
1点,2点,3点,4点,5点,6点
P(“出现偶数点”)=
方法探究
课堂训练
课堂小结
典型例题
基本概念
古典概型的概率计算公式:
(1)要判断所用概率模型是不是古典概型(前提)
在使用古典概型的概率公式时,应该注意:
P(A)=
(2)要找出随机事件A包含的基本事件的个数和试验中基本
事件的总数。
例2 先后抛掷两枚均匀的硬币,会出现几种结果?列举出来.
出现“一枚正面向上,一枚反面向上”的概率是多少?
解:基本事件有:
( 正 ,正 )( 正 ,反 )
( 反,正 )( 反 ,反)
P(A)=
典型例题
课堂训练
课堂小结
方法探究
基本概念
设A={一枚正面向上,一枚反面向上}
例3 先后掷两个均匀的骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是7的结果有多少种?
(3)向上的点数之和是7的概率是多少?
解:(1)掷一个骰子的结果有6种,我们把两个骰子标上记号1,2以便区分,它总共出现的情况如下表所示:
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
从表中可以看出同时掷两个骰子的结果共有36种。
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子 2号骰子
典型例题
课堂训练
课堂小结
方法探究
基本概念
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子 2号骰子
(2)在上面的结果中,向上的点数之和为7的结果有6种,分别为:
(3)由于所有36种结果是等可能的,其中向上点数之和为7的结果(记为事件A)有6种,因此,
(6,1),(5,2),(4,3),(3,4)(1,6),(2,5)
=
P(A)=
=
(6, 1)
(5, 2)
(4, 3)
(3, 4)
(2, 5)
(1, 6)
典型例题
课堂训练
课堂小结
方法探究
基本概念
为什么要把两个骰子标上记号?如果不标记号会出现什么情况?你能解释其中的原因吗?
如果不标上记号,类似于(3,6)和(6,3)的结果将没有区别。这时,所有可能的结果将是:
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子 2号骰子
(3,6)
(4,5)
因此,在投掷两个骰子的过程中,我们必须对两个骰子加以标号区分
(3,6)
(3,3)
概率不相等
?
概率相等吗?
课堂小结
典型例题
课堂训练
方法探究
2.
从1,2,3,4,5,6,7,8,9这九个自然数中任选一个,
所选中的数是3
的倍数的概率为
基本概念
3.
一副扑克牌,去掉大王和小王,在剩下的52张牌中随意抽出一张牌,
试求以下各个事件的概率:
A:
抽到一张Q
B:
抽到一张“梅花”
C:
抽到一张红桃 K
1.
单选题是标准化考试中常用的题型,一般是从A,B,C ,D
四个
选项中选择一个正确的答案。
假设考生不会做,他随机地选择了一个答案,则他
答对的概率为
1.
单选题是标准化考试中常用的题型,一般是从A,B,C,D
四个
选项中选择一个正确的答案。
假设考生不会做,他随机地选择了一个答案,则他答对的概率
为
课堂小结
典型例题
课堂训练
方法探究
基本概念
基本事件总共有几个?
“答对”包含几个基本事件?
4个:A,B,C,D
1个
课堂小结
典型例题
课堂训练
方法探究
2.
从
1,2,3,4,5,6,7,8,9
这九个自然数中任选一个,
所选中的数是3
的倍数的概率为
基本概念
3.
一副扑克牌,去掉大王和小王,在剩下的52张牌中随意抽出
一张牌,
试求以下各个事件的概率:
A:
抽到一张Q
B:
抽到一张“梅花”
C:
抽到一张红桃 K
2、练习1中如果该题是不定项选择题,假如考生也不会做,则他能够答对的
概率为多少?
此时比单选题容易了,还是更难了?
1、同时抛掷三枚均匀的硬币,会出现几种结果?
出现 “一枚正面向上,两枚反面向上”的概率是多少?
机动
练习
有限个
可能性
古典概型
基本事件
可能结果
基本事件数
课堂训练
典型例题
方法探究
基本概念
列举法(树状图或列表),应做到不重不漏。
(2)古典概型的定义和特点
(3)古典概型计算任何事件A的概率计算公式
(1)基本事件的两个特点:
1.知识点:
2. 基本事件计算的常用方法:
课堂小结
http://www.91taoke.com
谢谢观看!
第三章:概率
