选修1-1第二章圆锥曲线与方程 圆锥曲线中的斜率定值问题 课件 17张PPT
文档属性
| 名称 | 选修1-1第二章圆锥曲线与方程 圆锥曲线中的斜率定值问题 课件 17张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 404.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
圆锥曲线中斜率定值问题
人教A版选修1-1
高三专题复习
一、温故高考:
01
定值、定点问题是近几年高考的热点和难点问题之一,这类问题要求考生在变化的曲线或方程中找到不变的因素,即动中有静,静中有动,动中窥静,以静制动.
2015年全国卷1、卷2,2017年卷1、卷2,2018年卷1;
2015年陕西卷,2016年北京卷,山东卷等等
一轮复习要在研究历年高考的基础上,重新梳理和整合
所学的知识,挖掘、提炼蕴涵的思想方法,通过一道题解决
一类题,达到举一反三的效果.
02
二、课前导学:
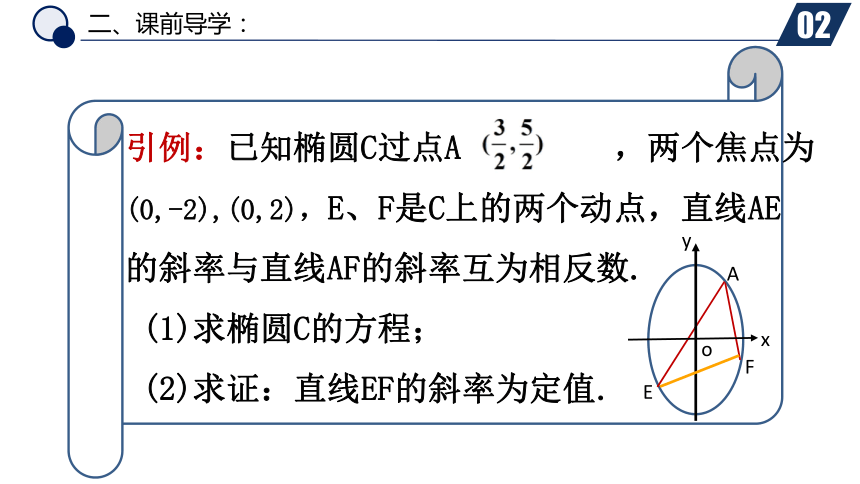
引例:已知椭圆C过点A ,两个焦点为
(0,-2),(0,2),E、F是C上的两个动点,直线AE
的斜率与直线AF的斜率互为相反数.
(1)求椭圆C的方程;
(2)求证:直线EF的斜率为定值.
A
F
E
x
y
o
03
二、课前导学:
解答:
法一:设出直线EF的方程
结合韦达定理,设而不求
法二:分别设直线AE的方程为
直线AF的方程为
法三:构造二次齐次式,结合韦达定理
几何画板演示
三、新知探究:
04
探究1:
如果改变A点的位置,动直线EF的斜率还会是定值吗?
几何画板演示
05
三、新知探究:
探究2:
如果改变直线AE与AF的斜率之和的值,动直线EF的斜率还会是定值吗?
Geogebra演示
06
三、新知探究:
探究3:
从前面的两个探究,能否得到一般性的结论呢?
07
三、新知探究:
结论1:
已知 是椭圆 上任意一点,设过点 的两条弦 的斜率为 ,
当 时,则直线 的斜率为定值;
当 时,则直线 过定点.
三、新知探究:
08
(2017全国卷1)已知椭圆C: ,四点
中恰有三点在椭圆C上.
(1)求椭圆C的方程;
(2)设直线 不经过 且与C相交于A,B两点.若直线
的斜率之和为-1,证明:直线 过定点
09
三、新知探究:
探究4:
能否把结论2推广到双曲线、抛物线?
Geogebra演示
10
三、新知探究:
探究5:
已知 是椭圆 上一个定点,设过点 的两条弦 的斜率为 , ,那么直线 又有什么规律呢?
Geogebra演示
11
三、新知探究:
结论3:
已知 是椭圆 上一个定点,设过点 的两条弦 的斜率为 ,
若 (定值),则直线 过定点;
12
三、新知探究:
(衡中卷)已知点 , ,动点 满足
设点 的轨迹为曲线C.
(1)求曲线C的方程;
(2)设 , 是曲线C上异于点 的两点,且直线 的斜率之积为定值2,求证:直线 恒过 定点.
Geogebra演示
13
三、新知探究:
结论4:
结论3可以推广到双曲线、抛物线.
Geogebra演示
14
四、归纳小结:
高考中圆锥曲线的特点是“多思少算、少想多算”,
平时应该学会发现问题,解决问题,善于思考和总结,
“一叶知秋”,从一道题推广到一类题;
学会证明圆锥曲线中两条弦的斜率和、斜率积为定值
的相关问题
15
五、布置作业:
整理本节课的内容,观看求斜率定值问题三种解法,并能灵活应用
完成课后作业(陕西卷、衡中卷的第20题)
感谢聆听 欢迎指正
THANKS FOR WATCHING
圆锥曲线中斜率定值问题
人教A版选修1-1
高三专题复习
一、温故高考:
01
定值、定点问题是近几年高考的热点和难点问题之一,这类问题要求考生在变化的曲线或方程中找到不变的因素,即动中有静,静中有动,动中窥静,以静制动.
2015年全国卷1、卷2,2017年卷1、卷2,2018年卷1;
2015年陕西卷,2016年北京卷,山东卷等等
一轮复习要在研究历年高考的基础上,重新梳理和整合
所学的知识,挖掘、提炼蕴涵的思想方法,通过一道题解决
一类题,达到举一反三的效果.
02
二、课前导学:
引例:已知椭圆C过点A ,两个焦点为
(0,-2),(0,2),E、F是C上的两个动点,直线AE
的斜率与直线AF的斜率互为相反数.
(1)求椭圆C的方程;
(2)求证:直线EF的斜率为定值.
A
F
E
x
y
o
03
二、课前导学:
解答:
法一:设出直线EF的方程
结合韦达定理,设而不求
法二:分别设直线AE的方程为
直线AF的方程为
法三:构造二次齐次式,结合韦达定理
几何画板演示
三、新知探究:
04
探究1:
如果改变A点的位置,动直线EF的斜率还会是定值吗?
几何画板演示
05
三、新知探究:
探究2:
如果改变直线AE与AF的斜率之和的值,动直线EF的斜率还会是定值吗?
Geogebra演示
06
三、新知探究:
探究3:
从前面的两个探究,能否得到一般性的结论呢?
07
三、新知探究:
结论1:
已知 是椭圆 上任意一点,设过点 的两条弦 的斜率为 ,
当 时,则直线 的斜率为定值;
当 时,则直线 过定点.
三、新知探究:
08
(2017全国卷1)已知椭圆C: ,四点
中恰有三点在椭圆C上.
(1)求椭圆C的方程;
(2)设直线 不经过 且与C相交于A,B两点.若直线
的斜率之和为-1,证明:直线 过定点
09
三、新知探究:
探究4:
能否把结论2推广到双曲线、抛物线?
Geogebra演示
10
三、新知探究:
探究5:
已知 是椭圆 上一个定点,设过点 的两条弦 的斜率为 , ,那么直线 又有什么规律呢?
Geogebra演示
11
三、新知探究:
结论3:
已知 是椭圆 上一个定点,设过点 的两条弦 的斜率为 ,
若 (定值),则直线 过定点;
12
三、新知探究:
(衡中卷)已知点 , ,动点 满足
设点 的轨迹为曲线C.
(1)求曲线C的方程;
(2)设 , 是曲线C上异于点 的两点,且直线 的斜率之积为定值2,求证:直线 恒过 定点.
Geogebra演示
13
三、新知探究:
结论4:
结论3可以推广到双曲线、抛物线.
Geogebra演示
14
四、归纳小结:
高考中圆锥曲线的特点是“多思少算、少想多算”,
平时应该学会发现问题,解决问题,善于思考和总结,
“一叶知秋”,从一道题推广到一类题;
学会证明圆锥曲线中两条弦的斜率和、斜率积为定值
的相关问题
15
五、布置作业:
整理本节课的内容,观看求斜率定值问题三种解法,并能灵活应用
完成课后作业(陕西卷、衡中卷的第20题)
感谢聆听 欢迎指正
THANKS FOR WATCHING
