3.1.2 导数的概念 课件 18张PPT
文档属性
| 名称 | 3.1.2 导数的概念 课件 18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 21:25:31 | ||
图片预览






文档简介
(共18张PPT)
导数的概念
人教A版实验教科书 选修1-1 第三章 第一节 第二课时《导数的概念》
探究:某高台跳水运动员距水面的高度与起跳后的时间存在函数关系:
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
如何解决这个问题?
(1)运动员在这段时间里是静止的吗?
一、复习回顾
计算运动员在 这段时间里的平均速度;
思考并回答下面的问题:
已知路程关于时间的函数,如何求运动物体在某时刻的瞬时速度呢?瞬时速度与平均速度是否有关呢?
瞬时速度:把运动物体在某一时刻的速度称为瞬时速度.
二、问题探究
测速仪如何在汽车通过的
瞬间测出瞬时速度?
利用激光反射测出指定时间内汽车的移动距离,通过计算得出这段时间的平均速度.测速时间非常短,因此可用这段时间的平均速度近似刻画这段时间内任意时刻的瞬时速度.
问题1.已知高台跳水运动员距水面的高度
与起跳后的时间 存在函数关系
求运动员在 时的瞬时速度.
分析:我们先考察在 附近的情况.
在 之后(或之前),任选一个时刻 , 计算 上的平均速度,在表格中填入数据.
二、问题探究
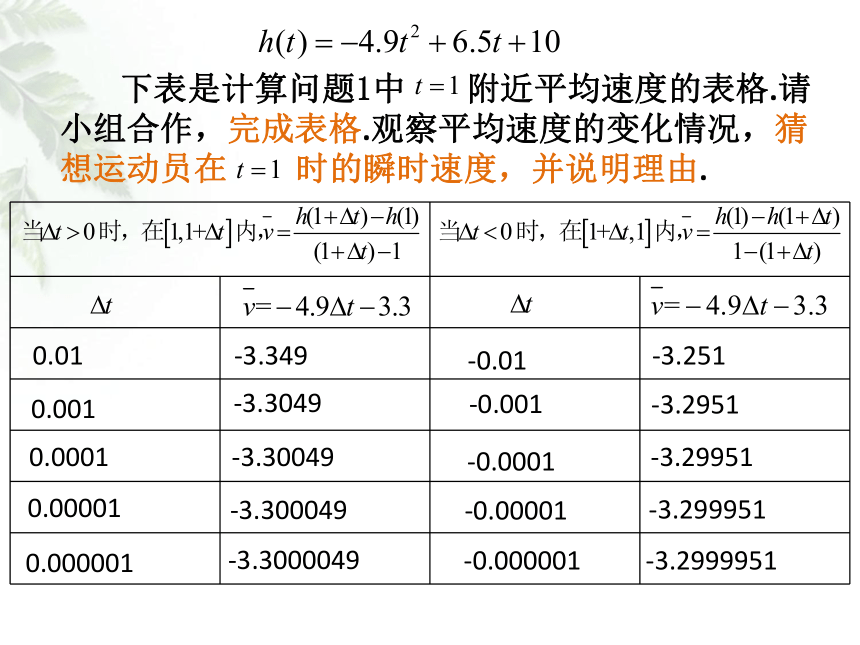
下表是计算问题1中 附近平均速度的表格.请小组合作,完成表格.观察平均速度的变化情况,猜想运动员在 时的瞬时速度,并说明理由.
-3.349
-3.3049
-3.30049
-3.300049
-3.3000049
-3.251
-3.2951
-3.29951
-3.299951
-3.2999951
0.01
0.001
0.0001
0.00001
0.000001
-0.01
-0.001
-0.0001
-0.00001
-0.000001
我们发现,当 趋近于 时,即无论 从小于
的一边,还是从大于 的一边趋近于 时,平均速
度都趋近于一个确定的值
从物理角度看,时间间隔 无限变小时,平均速度 就无限趋近于 时的瞬时速度.
因此,运动员在 时的瞬时速度是
求运动员在 时的瞬时速度.
我们发现,当 趋近于 时,平均速度都
趋近于一个确定的值
从物理角度看,时间间隔 无限变小时,平均速度 就无限趋近于 时的瞬时速度.
割线、切线位置关系
二、问题探究
问题2
分享课前作业:
收集你身边的“变化率”
从数学的角度思考上述5个实例,在“过程与方法”、“结果的形式”上有哪些共性?
过程与方法 结果的形式
1、用运动变化的观点研究问题;
2、应用了极限的思想;
3、用平均变化率逼近瞬时变化率.
1、结果都是一个确定的值;
2、具有一样的表现形式.
三、抽象概念 数学表达
三、抽象概念 数学表达
导数的概念
四、例题讲解
计算函数f(x)在x=x0处的导数
步骤:
例2 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为 f (x) = x2 – 7x+15 ( 0≤x≤8 ) . 计算第2h和第6h, 原油温度的瞬时变化率,并说明他们的意义.
根据导数的定义,
1.知识方面:
瞬时速度,切线斜率,导数概念
2.数学思想方法:
有限到无限的思考方法
逼近思想
特殊到一般
具体到抽象的思想
五、课堂小结
1. 请大家查阅相关资料,了解导数概念产生的背景与过程.
2. 结合上节课平均变化率的几何意义,请大家思考,导数的几何意义是什么?这是我们下一节要探究的问题.
六、布置作业
导数的概念
人教A版实验教科书 选修1-1 第三章 第一节 第二课时《导数的概念》
探究:某高台跳水运动员距水面的高度与起跳后的时间存在函数关系:
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
如何解决这个问题?
(1)运动员在这段时间里是静止的吗?
一、复习回顾
计算运动员在 这段时间里的平均速度;
思考并回答下面的问题:
已知路程关于时间的函数,如何求运动物体在某时刻的瞬时速度呢?瞬时速度与平均速度是否有关呢?
瞬时速度:把运动物体在某一时刻的速度称为瞬时速度.
二、问题探究
测速仪如何在汽车通过的
瞬间测出瞬时速度?
利用激光反射测出指定时间内汽车的移动距离,通过计算得出这段时间的平均速度.测速时间非常短,因此可用这段时间的平均速度近似刻画这段时间内任意时刻的瞬时速度.
问题1.已知高台跳水运动员距水面的高度
与起跳后的时间 存在函数关系
求运动员在 时的瞬时速度.
分析:我们先考察在 附近的情况.
在 之后(或之前),任选一个时刻 , 计算 上的平均速度,在表格中填入数据.
二、问题探究
下表是计算问题1中 附近平均速度的表格.请小组合作,完成表格.观察平均速度的变化情况,猜想运动员在 时的瞬时速度,并说明理由.
-3.349
-3.3049
-3.30049
-3.300049
-3.3000049
-3.251
-3.2951
-3.29951
-3.299951
-3.2999951
0.01
0.001
0.0001
0.00001
0.000001
-0.01
-0.001
-0.0001
-0.00001
-0.000001
我们发现,当 趋近于 时,即无论 从小于
的一边,还是从大于 的一边趋近于 时,平均速
度都趋近于一个确定的值
从物理角度看,时间间隔 无限变小时,平均速度 就无限趋近于 时的瞬时速度.
因此,运动员在 时的瞬时速度是
求运动员在 时的瞬时速度.
我们发现,当 趋近于 时,平均速度都
趋近于一个确定的值
从物理角度看,时间间隔 无限变小时,平均速度 就无限趋近于 时的瞬时速度.
割线、切线位置关系
二、问题探究
问题2
分享课前作业:
收集你身边的“变化率”
从数学的角度思考上述5个实例,在“过程与方法”、“结果的形式”上有哪些共性?
过程与方法 结果的形式
1、用运动变化的观点研究问题;
2、应用了极限的思想;
3、用平均变化率逼近瞬时变化率.
1、结果都是一个确定的值;
2、具有一样的表现形式.
三、抽象概念 数学表达
三、抽象概念 数学表达
导数的概念
四、例题讲解
计算函数f(x)在x=x0处的导数
步骤:
例2 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为 f (x) = x2 – 7x+15 ( 0≤x≤8 ) . 计算第2h和第6h, 原油温度的瞬时变化率,并说明他们的意义.
根据导数的定义,
1.知识方面:
瞬时速度,切线斜率,导数概念
2.数学思想方法:
有限到无限的思考方法
逼近思想
特殊到一般
具体到抽象的思想
五、课堂小结
1. 请大家查阅相关资料,了解导数概念产生的背景与过程.
2. 结合上节课平均变化率的几何意义,请大家思考,导数的几何意义是什么?这是我们下一节要探究的问题.
六、布置作业
