3.1.2 导数的概念 课件 26张PPT
文档属性
| 名称 | 3.1.2 导数的概念 课件 26张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 370.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
导数的概念
第二次数学危机
问题1:第二次数学危机发生的原因是什么?
问题2: 0与正无穷小是什么关系?相等吗
播放
导数的概念
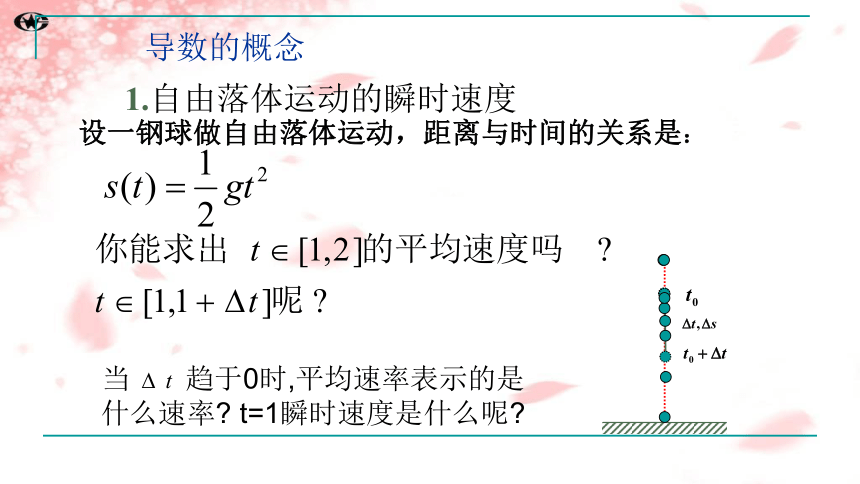
1.自由落体运动的瞬时速度
设一钢球做自由落体运动,距离与时间的关系是:
当 趋于0时,平均速率表示的是什么速率? t=1瞬时速度是什么呢?
如瞬时速度就是位移函数s(t)对时间t的导数.
是函数f(x)在以x0与x0+Δx 为端点的区间
[x0,x0+Δx](或[x0+Δx,x0])上的平均变化率,而导数则是函数f(x)在x0
处的变化率,它反映了函数随自变量变化而变化的快慢程度.
代表什么?
当点A(x2,y2)与B(x1,y1)比较接近时,直线AB 与曲线的关系又是什么
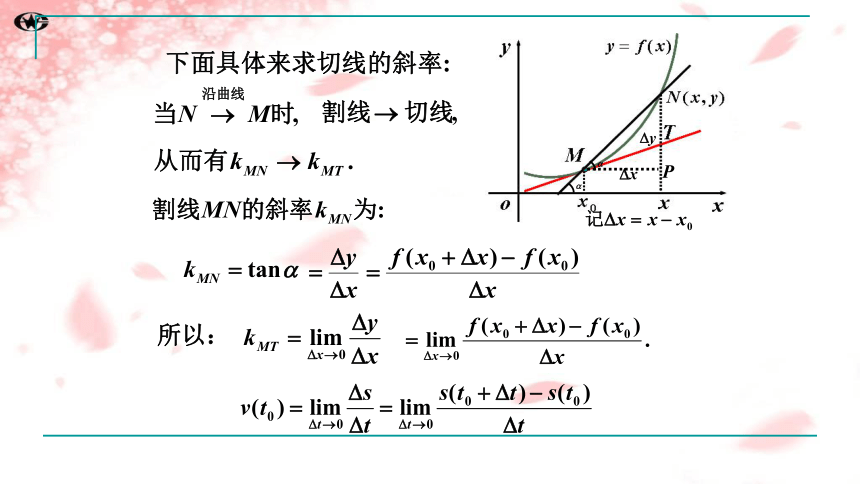
2.切线问题
割线的极限位置——切线.
播放
下面具体来求切线的斜率:
导数的几何意义
函数 y=f(x)在点x0处的导数的几何意义,就是曲线 y=f(x)在点P(x0 ,f(x0))处的切线的斜率,即曲线y=
f(x)在点P(x0 ,f(x0)) 处的切线的斜率是 .
故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:
例1:(1)求函数y=x2在x=2处的导数
(2)求函数y=1/x在x=4处的切线的斜率
(2)
由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:
注意:这里的增量不是一般意义上的增量,它可正也可负.
自变量的增量Δx的形式是多样的,但不论Δx选择
哪种形式, Δy也必须选择与之相对应的形式.
练习
求y=2x2+1在x=1处的导数
和切线的方程
要求导数很简单,
先求两个改变量,
两者相除求比值,
再对比值取极限。
小 结
P79-80,T2,T3
作业题
谢 谢
各 位 !
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
播放
导数的概念
第二次数学危机
问题1:第二次数学危机发生的原因是什么?
问题2: 0与正无穷小是什么关系?相等吗
播放
导数的概念
1.自由落体运动的瞬时速度
设一钢球做自由落体运动,距离与时间的关系是:
当 趋于0时,平均速率表示的是什么速率? t=1瞬时速度是什么呢?
如瞬时速度就是位移函数s(t)对时间t的导数.
是函数f(x)在以x0与x0+Δx 为端点的区间
[x0,x0+Δx](或[x0+Δx,x0])上的平均变化率,而导数则是函数f(x)在x0
处的变化率,它反映了函数随自变量变化而变化的快慢程度.
代表什么?
当点A(x2,y2)与B(x1,y1)比较接近时,直线AB 与曲线的关系又是什么
2.切线问题
割线的极限位置——切线.
播放
下面具体来求切线的斜率:
导数的几何意义
函数 y=f(x)在点x0处的导数的几何意义,就是曲线 y=f(x)在点P(x0 ,f(x0))处的切线的斜率,即曲线y=
f(x)在点P(x0 ,f(x0)) 处的切线的斜率是 .
故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:
例1:(1)求函数y=x2在x=2处的导数
(2)求函数y=1/x在x=4处的切线的斜率
(2)
由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:
注意:这里的增量不是一般意义上的增量,它可正也可负.
自变量的增量Δx的形式是多样的,但不论Δx选择
哪种形式, Δy也必须选择与之相对应的形式.
练习
求y=2x2+1在x=1处的导数
和切线的方程
要求导数很简单,
先求两个改变量,
两者相除求比值,
再对比值取极限。
小 结
P79-80,T2,T3
作业题
谢 谢
各 位 !
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
2.切线问题
播放
