3.4 生活中的优化问题举例 课件 19张PPT
文档属性
| 名称 | 3.4 生活中的优化问题举例 课件 19张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 21:10:47 | ||
图片预览




文档简介
(共19张PPT)
3.4 生活中的优化问题举例
人教A版2005新课标版高中数学选修1-1
马云
阿里巴巴创始人
阿里巴巴——中国最大的电商
王健林
万达创始人
万达公司——中国最大
的商业地产公司
马化腾
QQ·微信创始人
腾讯公司——中国最大
的互联网通信平台
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为优化问题.
七
十
载
拼
搏
坚
持
信
念
两
百
年
梦
想
不
忘
初
心
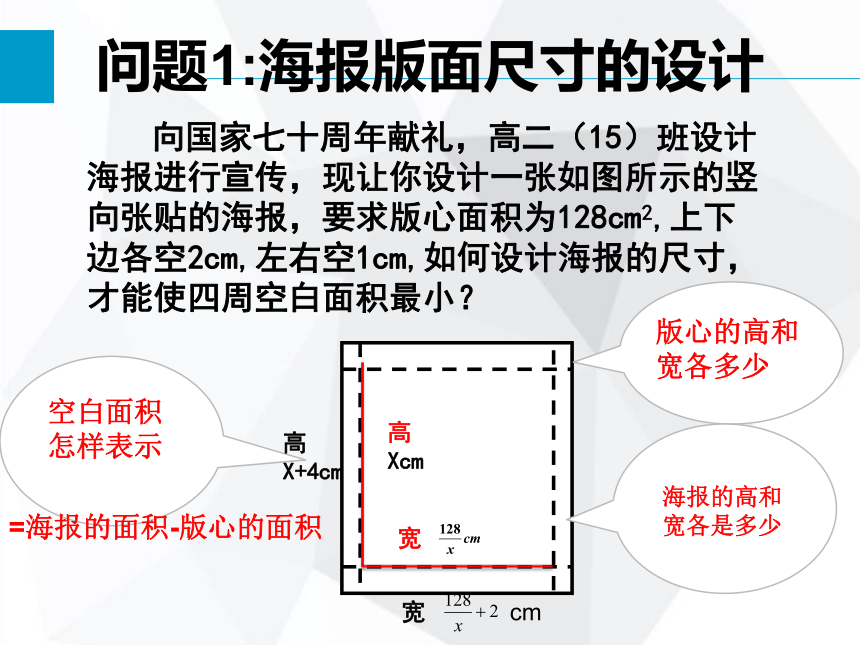
问题1:海报版面尺寸的设计
向国家七十周年献礼,高二(15)班设计海报进行宣传,现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128cm2,上下边各空2cm,左右空1cm,如何设计海报的尺寸,才能使四周空白面积最小?
=海报的面积-版心的面积
高
Xcm
高
X+4cm
宽
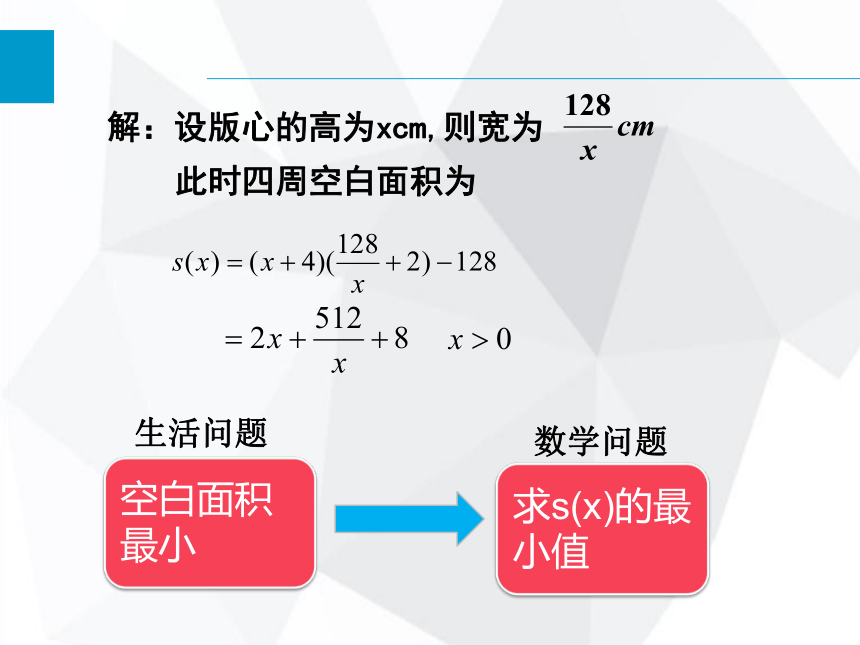
解:设版心的高为xcm,则宽为
此时四周空白面积为
因此,x=16是函数s(x)的极小值点,也是最小值点。
答:当版心高为16cm,宽为8cm时,海报四周空白面积最小。
求导数,有
解得,x=16 (x=-16)舍
〖归纳〗实际应用问题的解题程序
〖利用导数解决生活中的优化问题的步骤〗
问题2:饮料瓶大小对饮料公司利润有影响吗?
是不是饮料瓶越大,饮料公司的利润越大?你想从数学上知道它的道理吗?
大瓶饮料
2L 9元
小瓶饮料330mL2元
例2:某制造商制造并出售球形瓶装饮料.瓶子制造成本是0.8πr2分.已知每出售1ml的饮料,可获利0.2分,且瓶子的最大半径为6cm.
1)瓶子半径多大时,能使每瓶饮料的 利润最大?
2)瓶子半径多大时,每瓶饮料的利润最小?
解:由于瓶子的半径为r,所以每瓶饮料的利润是
当
当半径r<2时,f ’(r)<0 它表示 f(r) 单调递减,
即半径越大,利润越低.
当半径r>2时,f ’(r)>0它表示 f(r) 单调递增, 即半径越大,利润越高;
1、当半径为2cm时,利润最小,这时f(2)<0,
2、当半径为6cm时,利润最大。
从图中可以看出:
从图中,你还能看出什么吗?
练习:在边长为60cm的正方形铁皮的四角切去边长相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底铁皮箱.箱底边长为多少时,箱子容积最大?最大容积是多少?
x
h
h
x
h
h和x有怎样的等量关系?
2h+x=60
解 设箱底边长为 x,
箱子容积为
由
解得 x1=0 (舍), x2=40.
当x∈(0,40)时,V'(x)>0;当x∈(40,60)时,V'(x)<0.
∴函数V (x)在x=40处取得极大值,这个极大值就是函数V (x)的最大值.
答 当箱箱底边长为40cm时,箱子容积最大,
最大值为16000cm3
如何解决优化问题?
优化问题
优化问题的答案
用函数表示的数学问题
用导数解决数学问题
作业布置:
《作业本》P18 1,2,3
3.4 生活中的优化问题举例
人教A版2005新课标版高中数学选修1-1
马云
阿里巴巴创始人
阿里巴巴——中国最大的电商
王健林
万达创始人
万达公司——中国最大
的商业地产公司
马化腾
QQ·微信创始人
腾讯公司——中国最大
的互联网通信平台
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为优化问题.
七
十
载
拼
搏
坚
持
信
念
两
百
年
梦
想
不
忘
初
心
问题1:海报版面尺寸的设计
向国家七十周年献礼,高二(15)班设计海报进行宣传,现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128cm2,上下边各空2cm,左右空1cm,如何设计海报的尺寸,才能使四周空白面积最小?
=海报的面积-版心的面积
高
Xcm
高
X+4cm
宽
解:设版心的高为xcm,则宽为
此时四周空白面积为
因此,x=16是函数s(x)的极小值点,也是最小值点。
答:当版心高为16cm,宽为8cm时,海报四周空白面积最小。
求导数,有
解得,x=16 (x=-16)舍
〖归纳〗实际应用问题的解题程序
〖利用导数解决生活中的优化问题的步骤〗
问题2:饮料瓶大小对饮料公司利润有影响吗?
是不是饮料瓶越大,饮料公司的利润越大?你想从数学上知道它的道理吗?
大瓶饮料
2L 9元
小瓶饮料330mL2元
例2:某制造商制造并出售球形瓶装饮料.瓶子制造成本是0.8πr2分.已知每出售1ml的饮料,可获利0.2分,且瓶子的最大半径为6cm.
1)瓶子半径多大时,能使每瓶饮料的 利润最大?
2)瓶子半径多大时,每瓶饮料的利润最小?
解:由于瓶子的半径为r,所以每瓶饮料的利润是
当
当半径r<2时,f ’(r)<0 它表示 f(r) 单调递减,
即半径越大,利润越低.
当半径r>2时,f ’(r)>0它表示 f(r) 单调递增, 即半径越大,利润越高;
1、当半径为2cm时,利润最小,这时f(2)<0,
2、当半径为6cm时,利润最大。
从图中可以看出:
从图中,你还能看出什么吗?
练习:在边长为60cm的正方形铁皮的四角切去边长相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底铁皮箱.箱底边长为多少时,箱子容积最大?最大容积是多少?
x
h
h
x
h
h和x有怎样的等量关系?
2h+x=60
解 设箱底边长为 x,
箱子容积为
由
解得 x1=0 (舍), x2=40.
当x∈(0,40)时,V'(x)>0;当x∈(40,60)时,V'(x)<0.
∴函数V (x)在x=40处取得极大值,这个极大值就是函数V (x)的最大值.
答 当箱箱底边长为40cm时,箱子容积最大,
最大值为16000cm3
如何解决优化问题?
优化问题
优化问题的答案
用函数表示的数学问题
用导数解决数学问题
作业布置:
《作业本》P18 1,2,3
