3.4 生活中的优化问题举例 课件 31张PPT
文档属性
| 名称 | 3.4 生活中的优化问题举例 课件 31张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
目录
一、课题引入
二、新知探究
三、知识小结
五、作业布置
四、巩固练习
3.4 生活中的
优化问题举例
生活中经常遇到求利润最高,产量最大,成本最低,用料最省等实际问题,这些问题通常称为优化问题.解决优化问题的本质就是求函数的最值,因此,以函数为载体,以导数为工具,解决生活中的优化问题,是数学应用领域的一个重要课题.
探究一:
一条长为l的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,两段铁丝的长度分别是多少?
思考1:正方形的面积怎么计算?
思考2:两个正方形的边长与什么有关?
思考3:设两段铁丝的长度分别为x,l-x,则两个正方形的边长为什么?
思考4:设两正方形面积和为S(x),则S(x)的表达式是什么?
思考5:怎样求这个函数的最值?
解:设截成的两段铁丝的长度分别为x,l-x,则两个正方形面积之和为S(x)
建模关系式
列函数关系式
解模
作答
解决优化的问题的步骤:
探究(二):海报版面尺寸的设计
思考1:版心面积为定值128dm2,四周空白的面积怎么计算?
空白面积=海报的面积-版心的面积
建模关系式:
思考2:设版心的长为xdm,则海报的面积为多少?海报四周空白的面积为多少?
思考3:设海报四周空白的面积为S(x),则S(x)的最简表达式如何?其定义域是什么?
函数关系式:
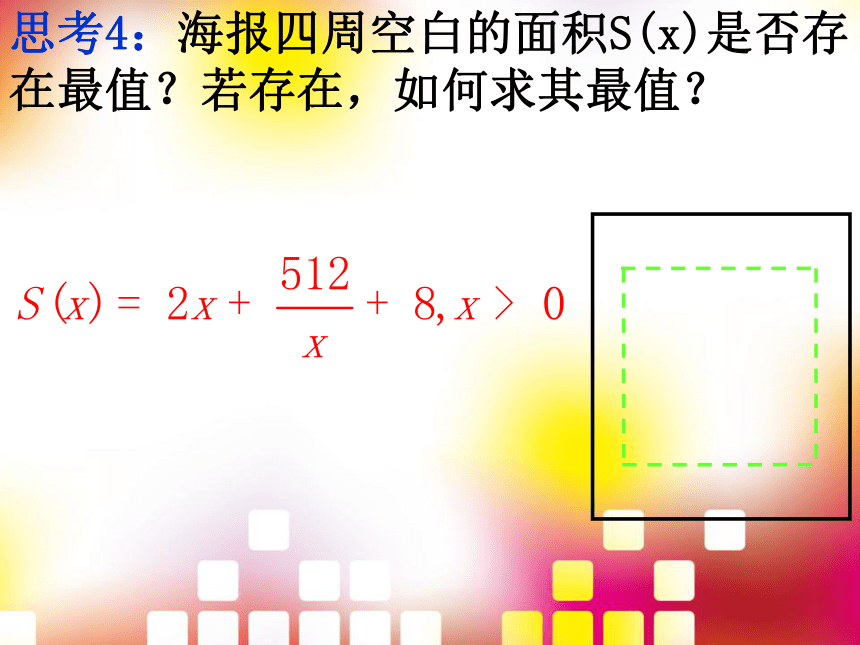
思考4:海报四周空白的面积S(x)是否存在最值?若存在,如何求其最值?
法一:均值不等式
(一正,二定,三相等)
解模:
法二:利用导数求函数的最值
答:当版心长为16dm,宽为8dm时,海报四周空白面积最小。
作答:
反思:对优化问题中的函数关系,要注意根据实际背景确定函数的定义域;如果目标函数在定义域内只有一个极值点,则这个极值点一般就是最值点.
探究(三):饮料瓶大小对饮料公司利 润的影响
是不是饮料瓶越大,饮料公司的利润越大?
思考1:利润怎样计算?
思考2:该题的收入,成本怎么样计算?
利润=收入-成本
建模关系式:
思考3:设每瓶满装饮料的利润为f(r),则函数f(r)的表达式和定义域是什么?
思考4:怎样求该函数的最值?
利用导数求解
函数关系式:
解:由于瓶子的半径为r,所以每瓶饮料的利润是
解模:
作答:
当0<r<3时,利润为负值;
当r=3时,利润为零;
当r>3时,利润为正值,并随着瓶子半径的增大利润也相应增大.
换一个角度:如果我们不用导数工具,直接从函数的图像上观察,会有什么发现?
小结:
解决优化问题的具体步骤:
一、建模关系式:读懂题意,分析寻找各个变量之间的关系。
二、列函数关系式:列出变量之间的函数关系式,注意一定要写出定义域
三、解模:利用函数的知识解决问题。要根据函数解析式的特点,用适当的方法求解。比如基本不等式、二次函数的图像、导数等
四、作答:题目怎么问,一般就怎么答。
动手试试:
练习:在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
一般情况下问题怎么问我们就怎么样设未知数
作业布置:
1.圆柱形金属饮料罐的容积一定时,它的高与底与半径应怎样选取,才能使所用的材料最省?
谢谢观赏!再见!
目录
一、课题引入
二、新知探究
三、知识小结
五、作业布置
四、巩固练习
3.4 生活中的
优化问题举例
生活中经常遇到求利润最高,产量最大,成本最低,用料最省等实际问题,这些问题通常称为优化问题.解决优化问题的本质就是求函数的最值,因此,以函数为载体,以导数为工具,解决生活中的优化问题,是数学应用领域的一个重要课题.
探究一:
一条长为l的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,两段铁丝的长度分别是多少?
思考1:正方形的面积怎么计算?
思考2:两个正方形的边长与什么有关?
思考3:设两段铁丝的长度分别为x,l-x,则两个正方形的边长为什么?
思考4:设两正方形面积和为S(x),则S(x)的表达式是什么?
思考5:怎样求这个函数的最值?
解:设截成的两段铁丝的长度分别为x,l-x,则两个正方形面积之和为S(x)
建模关系式
列函数关系式
解模
作答
解决优化的问题的步骤:
探究(二):海报版面尺寸的设计
思考1:版心面积为定值128dm2,四周空白的面积怎么计算?
空白面积=海报的面积-版心的面积
建模关系式:
思考2:设版心的长为xdm,则海报的面积为多少?海报四周空白的面积为多少?
思考3:设海报四周空白的面积为S(x),则S(x)的最简表达式如何?其定义域是什么?
函数关系式:
思考4:海报四周空白的面积S(x)是否存在最值?若存在,如何求其最值?
法一:均值不等式
(一正,二定,三相等)
解模:
法二:利用导数求函数的最值
答:当版心长为16dm,宽为8dm时,海报四周空白面积最小。
作答:
反思:对优化问题中的函数关系,要注意根据实际背景确定函数的定义域;如果目标函数在定义域内只有一个极值点,则这个极值点一般就是最值点.
探究(三):饮料瓶大小对饮料公司利 润的影响
是不是饮料瓶越大,饮料公司的利润越大?
思考1:利润怎样计算?
思考2:该题的收入,成本怎么样计算?
利润=收入-成本
建模关系式:
思考3:设每瓶满装饮料的利润为f(r),则函数f(r)的表达式和定义域是什么?
思考4:怎样求该函数的最值?
利用导数求解
函数关系式:
解:由于瓶子的半径为r,所以每瓶饮料的利润是
解模:
作答:
当0<r<3时,利润为负值;
当r=3时,利润为零;
当r>3时,利润为正值,并随着瓶子半径的增大利润也相应增大.
换一个角度:如果我们不用导数工具,直接从函数的图像上观察,会有什么发现?
小结:
解决优化问题的具体步骤:
一、建模关系式:读懂题意,分析寻找各个变量之间的关系。
二、列函数关系式:列出变量之间的函数关系式,注意一定要写出定义域
三、解模:利用函数的知识解决问题。要根据函数解析式的特点,用适当的方法求解。比如基本不等式、二次函数的图像、导数等
四、作答:题目怎么问,一般就怎么答。
动手试试:
练习:在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
一般情况下问题怎么问我们就怎么样设未知数
作业布置:
1.圆柱形金属饮料罐的容积一定时,它的高与底与半径应怎样选取,才能使所用的材料最省?
谢谢观赏!再见!
