3.4生活中的优化问题举例(第1课时) 课件 23张PPT
文档属性
| 名称 | 3.4生活中的优化问题举例(第1课时) 课件 23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 741.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
1.4 生活中的优化问题举例
(第1课时)
分析问题中各个变量之间的关系,建立适当的数学模型和函数关系,确定出函数的定义域,通过创造在定义域内求函数取值情境,即核心问题是建立适当的函数关系。再通过研究相应函数的性质,提出优化方案,使问题得以解决。在这个过程中,导数是一个有力的工具.
1.解决优化问题的方法:
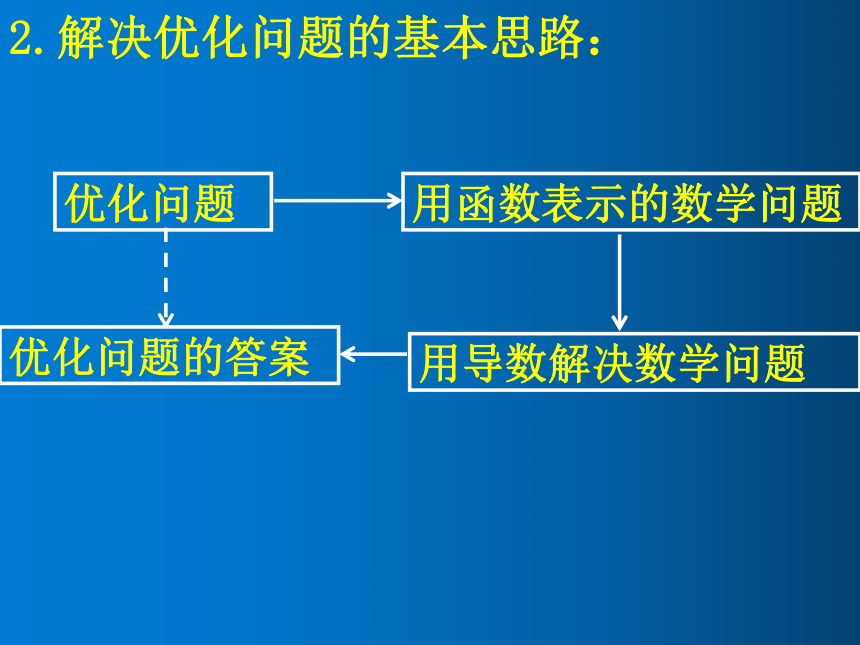
2.解决优化问题的基本思路:
优化问题
探究(一):与几何有关的最值问题
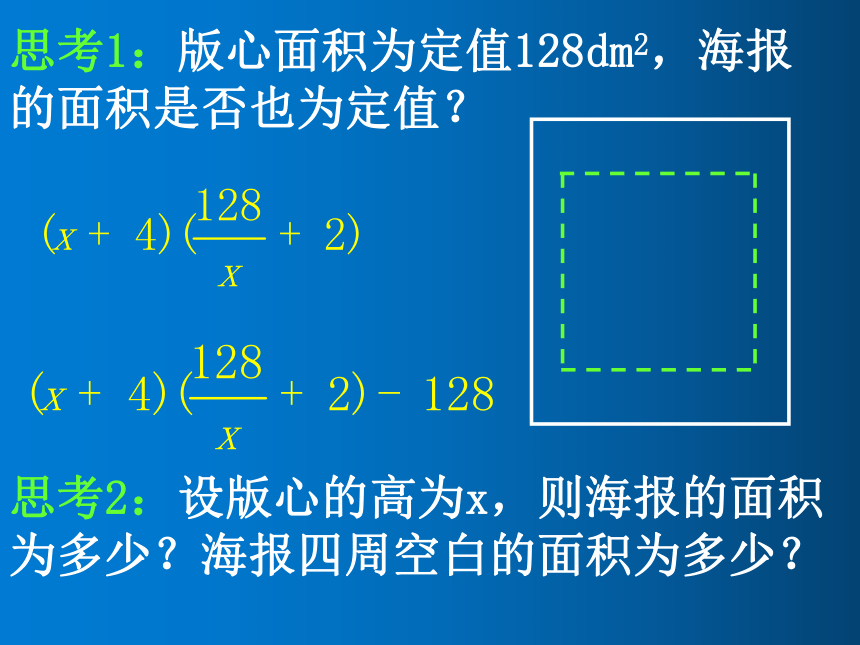
思考1:版心面积为定值128dm2,海报的面积是否也为定值?
思考2:设版心的高为x,则海报的面积为多少?海报四周空白的面积为多少?
思考3:设海报四周空白的面积为S(x),则S(x)的最简表达式如何?其定义域是什么?
思考4:海报四周空白的面积S(x)是否存在最值?若存在,如何求其最值?
思考5:如何设计海报的尺寸,才能使四周空白面积最小?
版心高为16dm, 宽为8dm时,
引申思考:在本题解法中,“是函数的极小值点,也是最小值点。”为什么?
一题多解:对于本题的最值你是否还有别的解法?
在实际问题中,一个函数在某个区间上若只有一个极值,则该极值即为这个区间上的最值。(常用于开区间或者无穷区间最值的求解)
反思 求最大(最小)值应用题的一般方法:
⑵ 确定函数的定义域,并求出极值点;
⑴ 分析问题中各量之间的关系,把实际问题化为数学问题,建立函数关系式;
⑶ 比较各极值与定义域端点函数的大小, 结合实际,确定最值或最值点.
跟踪训练1 在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
探究(二):与利润及其成本有关的最值问题
思考1:1mL饮料所占的体积是多少cm3?半径为r的瓶子最多能装多少mL的饮料?
思考2:每瓶满装的饮料的利润(单位:分)是多少?
思考3:设每瓶满装饮料的利润为f(r),则函数f(r)的定义域是什么?
(0,6]
当0<r<3时,利润为负值;当r=3时,利润为零;当r>3时,利润为正值,并随着瓶子半径的增大利润也相应增大.
思考6:市场上等量的小包装的物品一般比大包装的要贵些(如半斤装的白酒比一斤装的白酒平均价格要高),在数学上有什么道理?
将包装盒捏成球状,因为小包装的半径小,其利润低,生产商就提高销售价格来平衡与大包装的利润.
反思 解决此类有关利润的实际应用题,应灵活运用题设条件,建立利润的函数关系,常见的基本等量关系有
(1)利润=收入-成本;
(2)利润=每件产品的利润×销售件数
跟踪训练2 P37,习题1.4 A组,6
探究(三):效率最值问题
例3、磁盘的最大存储量问题
【背景知识】计算机把信息存储在磁盘上,磁盘是带有磁性介质的圆盘,并由操作系统将其格式化成磁道和扇区.磁道是指不同半径所构成的同心圆轨道,扇区是指被圆心角分割成的扇形区域.磁道上的定长的弧可作为基本存储单元,根据其磁化与否可分别记录数据0或1,这个基本单元通常称为比特,磁盘的构造如图所示.
为了保障磁盘的分辨率,磁道之间的宽度必须大于m,每比特所占用的磁道长度不得小于n.为了数据检索的方便,磁盘格式化时要求所有磁道具有相同的比特数(bit).
思考1:现有一张半径为R的磁盘,它的存储区是半径介于r与R的环形区域,且最外面的磁道不存储任何信息,那么这张磁盘的磁道数最多可达多少?
思考2:由于每条磁道上的比特数相同,那么这张磁盘存储量的大小取决于哪条磁道上的比特数?
最内一条磁道.
思考3:要使磁盘的存储量达到最大,那么最内一条磁道上的比特数为多少?
思考4:这张磁盘的存储量最大可达到多少比特?
课后思考:如果每条磁道存储的信息与磁道的长度成正比,那么如何计算磁盘的存储量?此时,是不是r越小,磁盘的存储量越大?
课堂小结:
1.解决优化问题的基本思路:
优化问题
2.解决优化问题的方法:通过分析问题中各个变量之间的关系,建立与其相应的数学模型,得到函数关系式,再通过研究相应函数的性质,提出优化方案,使问题得到解决.在这个过程中,导数往往是一个有利的工具。
作业布置:
课本P37,习题1.4 A组,5;
B组,1,2
1.4 生活中的优化问题举例
(第1课时)
分析问题中各个变量之间的关系,建立适当的数学模型和函数关系,确定出函数的定义域,通过创造在定义域内求函数取值情境,即核心问题是建立适当的函数关系。再通过研究相应函数的性质,提出优化方案,使问题得以解决。在这个过程中,导数是一个有力的工具.
1.解决优化问题的方法:
2.解决优化问题的基本思路:
优化问题
探究(一):与几何有关的最值问题
思考1:版心面积为定值128dm2,海报的面积是否也为定值?
思考2:设版心的高为x,则海报的面积为多少?海报四周空白的面积为多少?
思考3:设海报四周空白的面积为S(x),则S(x)的最简表达式如何?其定义域是什么?
思考4:海报四周空白的面积S(x)是否存在最值?若存在,如何求其最值?
思考5:如何设计海报的尺寸,才能使四周空白面积最小?
版心高为16dm, 宽为8dm时,
引申思考:在本题解法中,“是函数的极小值点,也是最小值点。”为什么?
一题多解:对于本题的最值你是否还有别的解法?
在实际问题中,一个函数在某个区间上若只有一个极值,则该极值即为这个区间上的最值。(常用于开区间或者无穷区间最值的求解)
反思 求最大(最小)值应用题的一般方法:
⑵ 确定函数的定义域,并求出极值点;
⑴ 分析问题中各量之间的关系,把实际问题化为数学问题,建立函数关系式;
⑶ 比较各极值与定义域端点函数的大小, 结合实际,确定最值或最值点.
跟踪训练1 在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
探究(二):与利润及其成本有关的最值问题
思考1:1mL饮料所占的体积是多少cm3?半径为r的瓶子最多能装多少mL的饮料?
思考2:每瓶满装的饮料的利润(单位:分)是多少?
思考3:设每瓶满装饮料的利润为f(r),则函数f(r)的定义域是什么?
(0,6]
当0<r<3时,利润为负值;当r=3时,利润为零;当r>3时,利润为正值,并随着瓶子半径的增大利润也相应增大.
思考6:市场上等量的小包装的物品一般比大包装的要贵些(如半斤装的白酒比一斤装的白酒平均价格要高),在数学上有什么道理?
将包装盒捏成球状,因为小包装的半径小,其利润低,生产商就提高销售价格来平衡与大包装的利润.
反思 解决此类有关利润的实际应用题,应灵活运用题设条件,建立利润的函数关系,常见的基本等量关系有
(1)利润=收入-成本;
(2)利润=每件产品的利润×销售件数
跟踪训练2 P37,习题1.4 A组,6
探究(三):效率最值问题
例3、磁盘的最大存储量问题
【背景知识】计算机把信息存储在磁盘上,磁盘是带有磁性介质的圆盘,并由操作系统将其格式化成磁道和扇区.磁道是指不同半径所构成的同心圆轨道,扇区是指被圆心角分割成的扇形区域.磁道上的定长的弧可作为基本存储单元,根据其磁化与否可分别记录数据0或1,这个基本单元通常称为比特,磁盘的构造如图所示.
为了保障磁盘的分辨率,磁道之间的宽度必须大于m,每比特所占用的磁道长度不得小于n.为了数据检索的方便,磁盘格式化时要求所有磁道具有相同的比特数(bit).
思考1:现有一张半径为R的磁盘,它的存储区是半径介于r与R的环形区域,且最外面的磁道不存储任何信息,那么这张磁盘的磁道数最多可达多少?
思考2:由于每条磁道上的比特数相同,那么这张磁盘存储量的大小取决于哪条磁道上的比特数?
最内一条磁道.
思考3:要使磁盘的存储量达到最大,那么最内一条磁道上的比特数为多少?
思考4:这张磁盘的存储量最大可达到多少比特?
课后思考:如果每条磁道存储的信息与磁道的长度成正比,那么如何计算磁盘的存储量?此时,是不是r越小,磁盘的存储量越大?
课堂小结:
1.解决优化问题的基本思路:
优化问题
2.解决优化问题的方法:通过分析问题中各个变量之间的关系,建立与其相应的数学模型,得到函数关系式,再通过研究相应函数的性质,提出优化方案,使问题得到解决.在这个过程中,导数往往是一个有利的工具。
作业布置:
课本P37,习题1.4 A组,5;
B组,1,2
