选修1-1 第三章导数及其应用 课件 18张PPT
文档属性
| 名称 | 选修1-1 第三章导数及其应用 课件 18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第三章 导数及其应用复习小结
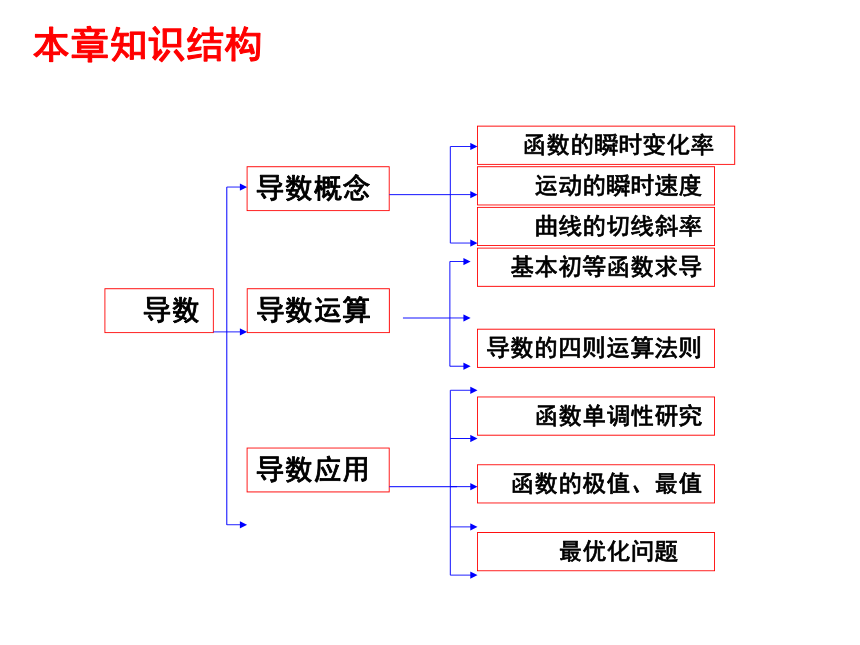
本章知识结构
导数
导数概念
导数运算
导数应用
函数的瞬时变化率
运动的瞬时速度
曲线的切线斜率
基本初等函数求导
导数的四则运算法则
函数单调性研究
函数的极值、最值
最优化问题
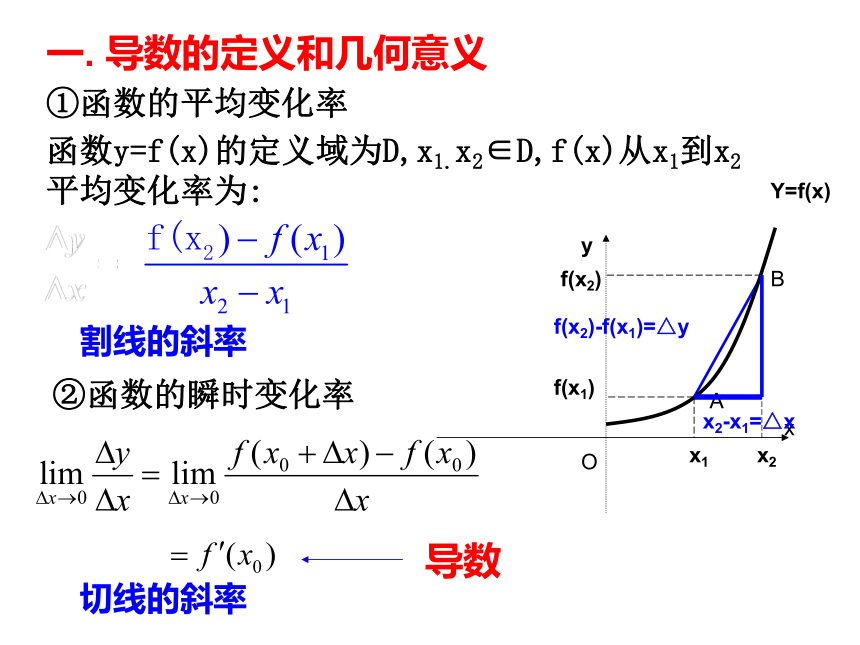
一. 导数的定义和几何意义
①函数的平均变化率
函数y=f(x)的定义域为D,x1.x2∈D,f(x)从x1到x2平均变化率为:
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
②函数的瞬时变化率
导数
割线的斜率
切线的斜率
过p(x0,y0)作一曲线的切线方程
1) p(x0,y0)为切点
2)p(x0,y0)不为切点
切线方程
二.对基本初等函数的导数公式的应用
三.导数的基本运算
四.导数的应用
(1)单调性区间
1) 如果恒有 f′(x)≥0,那么 y=f(x) 在这个区间(a,b)内单调递增;
2) 如果恒有 f′(x)≤0,那么 y=f(x)在这个区间(a,b)内单调递减。
一般地,函数y=f(x)在某个区间(a,b)内
已知三次函数f(x)=ax3+bx2+cx+d(x∈R)
的导数为
f‘(x)=3ax2+2bx+c
(1)有三个单调区间
(2)有极大值和极小值
(3)有极值
(4)仅有一个单调区间
(5)没有极值
(2)极值与最值
2)如果a是f’(x)=0的一个根,并且在a 的左侧附近f’(x)<0,在a 右侧附近f’(x)>0,那么是f(a)函数f(x)的一个极小值.
1)如果b是f’(x)=0的一个根,并且在b左侧附近f’(x)>0,在b右侧附近f’(x)<0,那么f(b)是函数f(x)的一个极大值
注:导数等于零的点不一定是极值点.
在闭区间[a,b]上的函数y=f(x)的图象是一条连续不断的曲线,则它必有最大值和最小值.
函数的最大(小)值与导数
五.题型讲解
题型一:导数的几何意义,求切线方程
1、
例3.
D
题型三 .讨论函数单调性,求单调区间区间
例1:(1)讨论函数 的单调性,并求单调区间
(2)讨论函数 的单调性.
.
变量分离法
2.
变量分离法
2.
恒成立
;
恒成立
将含参数的恒成立式子中的参数分离出来,化成形如:
或
或
恒成立的形式.
恒成立
的范围是
的值域;
则
若在等式或不等式中出现两个变量,其中一个变量的范围已知,另一个变量的范围为所求,且容易通过恒等变形将两个变量分别置于等号或不等号的两边,则可将恒成立问题转化成函数的最值问题求解.
已知函数f(x)=ax -lnx . 若f(x)>1在 (1,+∞)上恒成立,求a的取值范围.
解题依据:
(1)a≥f(x)恒成立
(2)a≤f(x)恒成立
一、利用分离参数法解决恒成立问题
典例分析
课堂小结:
这节课你有什么收获?
作业设计:
习题
第三章 导数及其应用复习小结
本章知识结构
导数
导数概念
导数运算
导数应用
函数的瞬时变化率
运动的瞬时速度
曲线的切线斜率
基本初等函数求导
导数的四则运算法则
函数单调性研究
函数的极值、最值
最优化问题
一. 导数的定义和几何意义
①函数的平均变化率
函数y=f(x)的定义域为D,x1.x2∈D,f(x)从x1到x2平均变化率为:
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
②函数的瞬时变化率
导数
割线的斜率
切线的斜率
过p(x0,y0)作一曲线的切线方程
1) p(x0,y0)为切点
2)p(x0,y0)不为切点
切线方程
二.对基本初等函数的导数公式的应用
三.导数的基本运算
四.导数的应用
(1)单调性区间
1) 如果恒有 f′(x)≥0,那么 y=f(x) 在这个区间(a,b)内单调递增;
2) 如果恒有 f′(x)≤0,那么 y=f(x)在这个区间(a,b)内单调递减。
一般地,函数y=f(x)在某个区间(a,b)内
已知三次函数f(x)=ax3+bx2+cx+d(x∈R)
的导数为
f‘(x)=3ax2+2bx+c
(1)有三个单调区间
(2)有极大值和极小值
(3)有极值
(4)仅有一个单调区间
(5)没有极值
(2)极值与最值
2)如果a是f’(x)=0的一个根,并且在a 的左侧附近f’(x)<0,在a 右侧附近f’(x)>0,那么是f(a)函数f(x)的一个极小值.
1)如果b是f’(x)=0的一个根,并且在b左侧附近f’(x)>0,在b右侧附近f’(x)<0,那么f(b)是函数f(x)的一个极大值
注:导数等于零的点不一定是极值点.
在闭区间[a,b]上的函数y=f(x)的图象是一条连续不断的曲线,则它必有最大值和最小值.
函数的最大(小)值与导数
五.题型讲解
题型一:导数的几何意义,求切线方程
1、
例3.
D
题型三 .讨论函数单调性,求单调区间区间
例1:(1)讨论函数 的单调性,并求单调区间
(2)讨论函数 的单调性.
.
变量分离法
2.
变量分离法
2.
恒成立
;
恒成立
将含参数的恒成立式子中的参数分离出来,化成形如:
或
或
恒成立的形式.
恒成立
的范围是
的值域;
则
若在等式或不等式中出现两个变量,其中一个变量的范围已知,另一个变量的范围为所求,且容易通过恒等变形将两个变量分别置于等号或不等号的两边,则可将恒成立问题转化成函数的最值问题求解.
已知函数f(x)=ax -lnx . 若f(x)>1在 (1,+∞)上恒成立,求a的取值范围.
解题依据:
(1)a≥f(x)恒成立
(2)a≤f(x)恒成立
一、利用分离参数法解决恒成立问题
典例分析
课堂小结:
这节课你有什么收获?
作业设计:
习题
