1.2 独立性检验的基本思想及其初步应用 课件 18张PPT
文档属性
| 名称 | 1.2 独立性检验的基本思想及其初步应用 课件 18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
1.2 独立性检验的基本思想及应用
有人说:吸烟有害健康!吸烟会引发肺癌.
另一些人说:吸烟不影响健康.理由是,有的吸烟老人却很长寿。
这两种观点哪个正确呢?
问题导入,激发兴趣
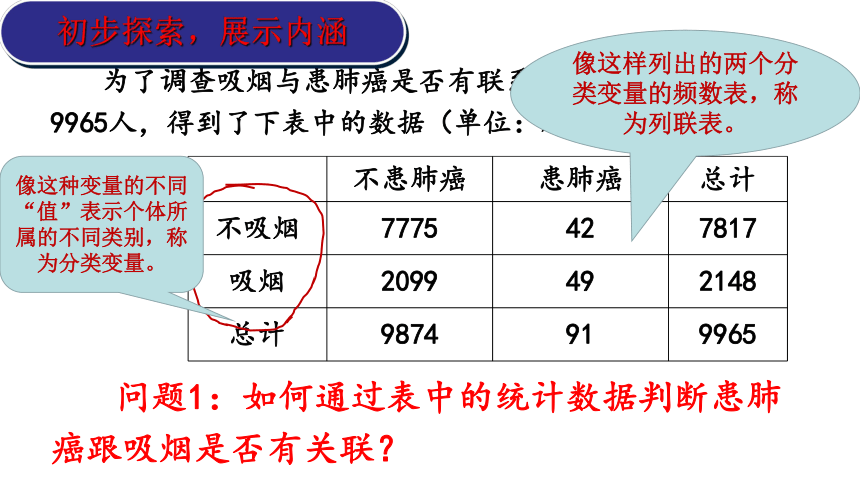
为了调查吸烟与患肺癌是否有联系,某机构随机调查了
9965人,得到了下表中的数据(单位:人)
问题1:如何通过表中的统计数据判断患肺
癌跟吸烟是否有关联?
初步探索,展示内涵
像这种变量的不同“值”表示个体所属的不同类别,称为分类变量。
像这样列出的两个分类变量的频数表,称为列联表。
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
由以上列联表,我们估计①在不吸烟者中患肺癌的比例为________;
②在吸烟者中患肺癌的比例为 。
等高条形图
形象直观
粗略估计
初步探索,展示内涵
还有其它方法来判断吸烟和患肺癌有关呢?
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
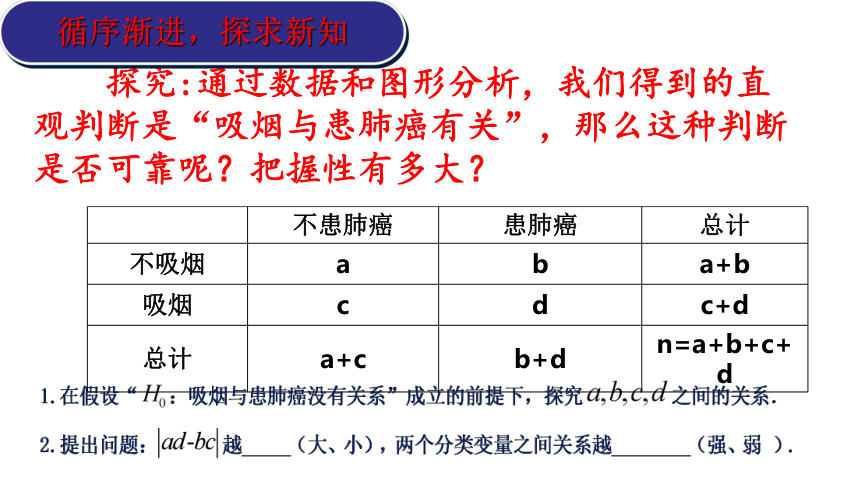
探究:通过数据和图形分析,我们得到的直观判断是“吸烟与患肺癌有关”,那么这种判断是否可靠呢?把握性有多大?
循序渐进,探求新知
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d n=a+b+c+d
合作探究
请同学们精读教材P11到P12,小组合作回答以下四个问题:
独立性检验的基本思想
判断分类变量A与B之间是否有关
结果有两种可能:有关或无关
在一次试验中,小概率事件几乎是不可能发生的
对立与统一的辩证思想
反证法 独立性检验
目 标 证明结论成立(只有一种)
两种
情况
理论
依据 矛盾双方不可能同时成立
但是有且只有一个成立
操作
步骤
结论:我们有99.9%的把握认为患肺癌与吸烟有关联。因此,为了健康你、我、他,我们要拒绝吸烟、劝诫他人不要吸烟!
问题6:在吸烟和患肺癌的例子中,请根据卡方
的值,并结合临界值表,说说你得到了什么结论
和启发?
应用感悟,思想升华
课堂活动:
请根据你的实际情况,做出真实的选择
选项1.男生、喜欢足球
选项2.男生、不喜欢足球
选项3.女生、喜欢足球
选项4.女生、不喜欢足球
算一算:请同学们根据统计数据,回答你有多大把握认为喜欢足球与性别之间有关联。
喜欢足球 不喜欢足球 合计
男生
女生
合计
问题7:这组数据采集于我们班这个小范围内,为了使得结论更客观、更可靠,我们应该做何改进?
通过本节课的学习,谈谈你的收获。
(关键词:知识、能力、数学思想方法)
如:“吸烟与患肺癌有关系”,但这种判断会犯错误,犯错误的概率不会超过0.01.
独立性检验的一般步骤
不患肺癌 患肺癌 合计
不吸烟
吸烟
合计
数据分析
直观想象、直观判断
数学运算
数学抽象数学建模逻辑推理
归纳总结,素养提升
课后作业:
1、校本作业
2、思考题
思考反证法原理与独立性检验原理的区别与联系。
3、调查本校高二年学生,判断性别与喜欢数学之间是否有关?
友情提醒:课堂上还未完全掌握的同学还可以通过扫描下方的二维码观看本节课微课视频哦!
在终极的分析中,一切知识都是历史;
在抽象的意义下,一切科学都是数学;
在理性的世界里,所有的判断都是统计学.
著名统计学家——C.R.Rao
1.2 独立性检验的基本思想及应用
有人说:吸烟有害健康!吸烟会引发肺癌.
另一些人说:吸烟不影响健康.理由是,有的吸烟老人却很长寿。
这两种观点哪个正确呢?
问题导入,激发兴趣
为了调查吸烟与患肺癌是否有联系,某机构随机调查了
9965人,得到了下表中的数据(单位:人)
问题1:如何通过表中的统计数据判断患肺
癌跟吸烟是否有关联?
初步探索,展示内涵
像这种变量的不同“值”表示个体所属的不同类别,称为分类变量。
像这样列出的两个分类变量的频数表,称为列联表。
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
由以上列联表,我们估计①在不吸烟者中患肺癌的比例为________;
②在吸烟者中患肺癌的比例为 。
等高条形图
形象直观
粗略估计
初步探索,展示内涵
还有其它方法来判断吸烟和患肺癌有关呢?
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
探究:通过数据和图形分析,我们得到的直观判断是“吸烟与患肺癌有关”,那么这种判断是否可靠呢?把握性有多大?
循序渐进,探求新知
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d n=a+b+c+d
合作探究
请同学们精读教材P11到P12,小组合作回答以下四个问题:
独立性检验的基本思想
判断分类变量A与B之间是否有关
结果有两种可能:有关或无关
在一次试验中,小概率事件几乎是不可能发生的
对立与统一的辩证思想
反证法 独立性检验
目 标 证明结论成立(只有一种)
两种
情况
理论
依据 矛盾双方不可能同时成立
但是有且只有一个成立
操作
步骤
结论:我们有99.9%的把握认为患肺癌与吸烟有关联。因此,为了健康你、我、他,我们要拒绝吸烟、劝诫他人不要吸烟!
问题6:在吸烟和患肺癌的例子中,请根据卡方
的值,并结合临界值表,说说你得到了什么结论
和启发?
应用感悟,思想升华
课堂活动:
请根据你的实际情况,做出真实的选择
选项1.男生、喜欢足球
选项2.男生、不喜欢足球
选项3.女生、喜欢足球
选项4.女生、不喜欢足球
算一算:请同学们根据统计数据,回答你有多大把握认为喜欢足球与性别之间有关联。
喜欢足球 不喜欢足球 合计
男生
女生
合计
问题7:这组数据采集于我们班这个小范围内,为了使得结论更客观、更可靠,我们应该做何改进?
通过本节课的学习,谈谈你的收获。
(关键词:知识、能力、数学思想方法)
如:“吸烟与患肺癌有关系”,但这种判断会犯错误,犯错误的概率不会超过0.01.
独立性检验的一般步骤
不患肺癌 患肺癌 合计
不吸烟
吸烟
合计
数据分析
直观想象、直观判断
数学运算
数学抽象数学建模逻辑推理
归纳总结,素养提升
课后作业:
1、校本作业
2、思考题
思考反证法原理与独立性检验原理的区别与联系。
3、调查本校高二年学生,判断性别与喜欢数学之间是否有关?
友情提醒:课堂上还未完全掌握的同学还可以通过扫描下方的二维码观看本节课微课视频哦!
在终极的分析中,一切知识都是历史;
在抽象的意义下,一切科学都是数学;
在理性的世界里,所有的判断都是统计学.
著名统计学家——C.R.Rao
