选修1-2 第一章 统计案例 小结 课件 39张PPT
文档属性
| 名称 | 选修1-2 第一章 统计案例 小结 课件 39张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览








文档简介
(共39张PPT)
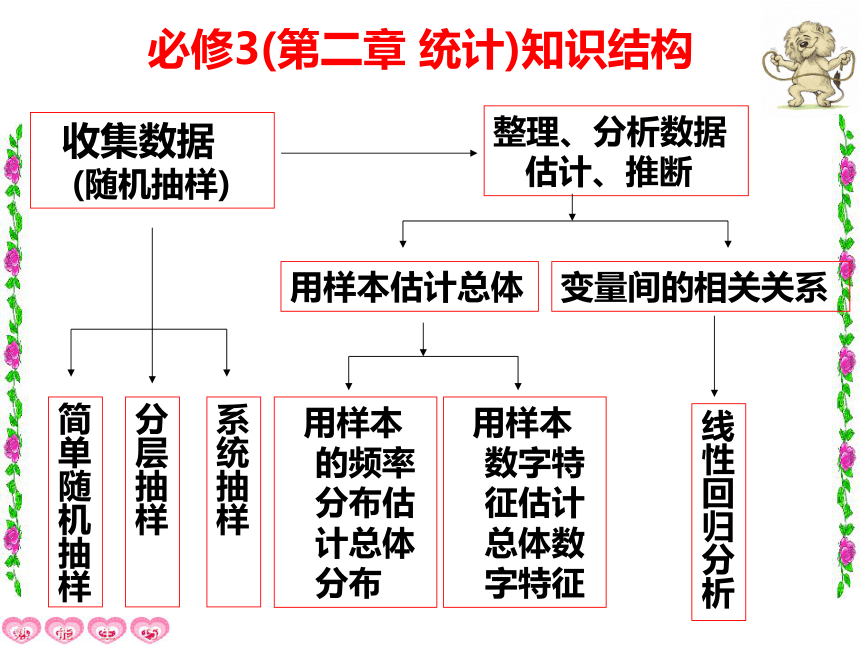
必修3(第二章 统计)知识结构
收集数据 (随机抽样)
整理、分析数据估计、推断
简单随机抽样
分层抽样
系统抽样
用样本估计总体
变量间的相关关系
用样本的频率分布估计总体分布
用样本数字特征估计总体数字特征
线性回归分析
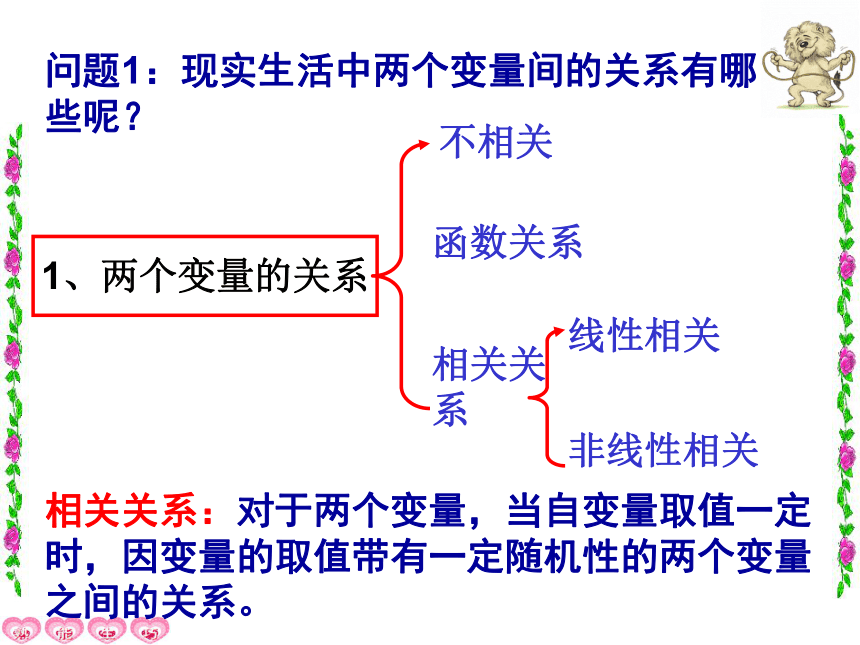
1、两个变量的关系
不相关
相关关系
函数关系
线性相关
非线性相关
问题1:现实生活中两个变量间的关系有哪些呢?
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。
问题2:对于线性相关的两个变量用什么方法来刻划之间的关系呢?
2、最小二乘估计
最小二乘估计下的线性回归方程:
回归直线必过样本点的中心
3、回归分析的基本步骤:
(1) 选变量,(解释变量,预报变量)
(2)画散点图
(3)选模型
(4)估计参数
(5)分析和预测
回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
该类题属于线性回归问题,解答本类题目的关键首先应先通过散点图来分析两变量间的关系是否相关,然后再利用求回归方程的公式求解回归方程.
例题1 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
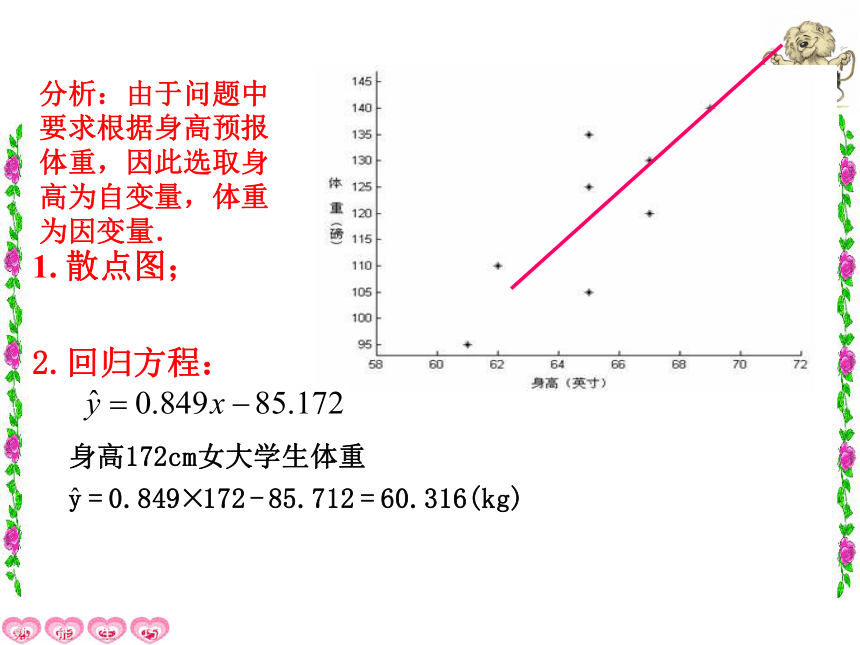
1. 散点图;
2.回归方程:
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
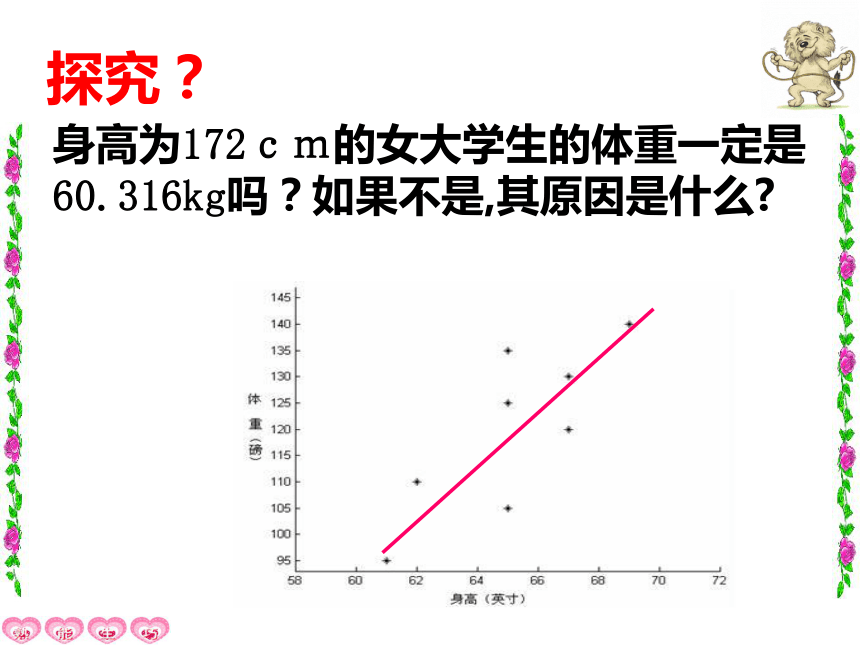
探究?
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,其原因是什么?
残差分析
以纵坐标为残差,横坐标为编号,作出图形(残差图)来分析残差特性.
由图可知,第1个样本点和第6个样本点的残差比较大,需要确认在采集这两个样本点的过程中是否有人为的错误.如果数据采集有错误,就予以纠正,然后重新利用线性回归模型拟合数据;如果数据采集没有错误,则需要寻找其他原因.
问:如何刻画模型拟合的精度?
相关指数:
(1)R2取值越大(越接近1),模型的拟合效果越好.
(2)在例1中我们可以求出R2=0.64,表明:“女大学生的身高解释了64%的体重变化”,或者说“女大学生的体重差异有64%是由身高引起的”。
问题四:结合例1思考:用回归方程预报体重时应注意什么?
1.回归方程只适用于我们所研究的样本的总体。
2.我们建立的回归方程一般都有时间性。
3.不能期望回归方程得到的预报值就是预报变量的精确值。
例2 一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据列于表中:
试建立产卵数y与温度x之间的回归方程;
方法一:一元函数模型
产卵数
气温
变换 y=bx+a
非线性关系 线性关系
对数
方法三:指数函数模型
由计算器得:z关于x的线性回归方程
因此y关于x的非线性回归方程为
当x=28 时,y ≈44 ,指数回归模型比二次函数模型更好
温度x/ 21 23 25 27
Z=lny 1.946 2.398 3.405 3.178
产卵数y/个 7 11 21 24
29 32 35
4.190 4.745 5.784
66 115 325
1)确定解释变量和预报变量;
2)画出散点图;
3)确定回归方程类型;
4)求出回归方程;
5)利用相关指数或残差进行分析.
对两个分类变量的相关关系的分析方法:
①通过图形直观判断两个分类变量是否相关;
②独立性检验.
由列联表可以粗略估计出,在不吸烟者中,有0.54%患有肺癌;在吸烟者中,有2.28%患有肺癌。因此,直观上可以得到结论:吸烟者和不吸烟者患肺癌的可能性存在差异.
为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人):
吸烟与患肺癌列联表:
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
1、列联表
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
2、等高条形图
等高条形图更清晰地表达了两种情况下患肺癌的比例.
独立性检验:
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
为了使不同样本容量的数据有统一的评判标准,我们构造一个随机变量
由列联表中数据,利用公式(1)计算得K2的观测值为:
(1)
其中n=a+b+c+d为样本容量.
我们在犯错误概率不超过0.01的前提下,认为“吸烟与患肺癌有关系”.
(1)如果k>10.828,就有99.9%的把握认为“X与Y有关系”;
(2)如果k>6.635,就有99%的把握认为“X与Y有关系”;
(3)如果k>2.706,就有90%的把握认为“X与Y有关系”;
(4)如果k<=2.706,就认为没有充分的证据显示
“X与Y有关系”.
临界值
例2 为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中随机抽取60名学生,得到如下列联表:
在多大程度上可以认为高中生的性别与是否喜欢数学课程之间有关系?为什么?
喜欢数学课程 不喜欢数学课程 总计
男 24 16 40
女 15 5 20
总计 39 21 60
计算得K2的观测值为:
我们有99%的把握认为高中生的性别与是否喜欢数学课程之间有关系。
课堂小结:
一:回归分析的基本思想和应用
二:独立性检验的基本思想和应用
练习:
作业:习题1.2
必修3(第二章 统计)知识结构
收集数据 (随机抽样)
整理、分析数据估计、推断
简单随机抽样
分层抽样
系统抽样
用样本估计总体
变量间的相关关系
用样本的频率分布估计总体分布
用样本数字特征估计总体数字特征
线性回归分析
1、两个变量的关系
不相关
相关关系
函数关系
线性相关
非线性相关
问题1:现实生活中两个变量间的关系有哪些呢?
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。
问题2:对于线性相关的两个变量用什么方法来刻划之间的关系呢?
2、最小二乘估计
最小二乘估计下的线性回归方程:
回归直线必过样本点的中心
3、回归分析的基本步骤:
(1) 选变量,(解释变量,预报变量)
(2)画散点图
(3)选模型
(4)估计参数
(5)分析和预测
回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
该类题属于线性回归问题,解答本类题目的关键首先应先通过散点图来分析两变量间的关系是否相关,然后再利用求回归方程的公式求解回归方程.
例题1 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
1. 散点图;
2.回归方程:
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
探究?
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,其原因是什么?
残差分析
以纵坐标为残差,横坐标为编号,作出图形(残差图)来分析残差特性.
由图可知,第1个样本点和第6个样本点的残差比较大,需要确认在采集这两个样本点的过程中是否有人为的错误.如果数据采集有错误,就予以纠正,然后重新利用线性回归模型拟合数据;如果数据采集没有错误,则需要寻找其他原因.
问:如何刻画模型拟合的精度?
相关指数:
(1)R2取值越大(越接近1),模型的拟合效果越好.
(2)在例1中我们可以求出R2=0.64,表明:“女大学生的身高解释了64%的体重变化”,或者说“女大学生的体重差异有64%是由身高引起的”。
问题四:结合例1思考:用回归方程预报体重时应注意什么?
1.回归方程只适用于我们所研究的样本的总体。
2.我们建立的回归方程一般都有时间性。
3.不能期望回归方程得到的预报值就是预报变量的精确值。
例2 一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据列于表中:
试建立产卵数y与温度x之间的回归方程;
方法一:一元函数模型
产卵数
气温
变换 y=bx+a
非线性关系 线性关系
对数
方法三:指数函数模型
由计算器得:z关于x的线性回归方程
因此y关于x的非线性回归方程为
当x=28 时,y ≈44 ,指数回归模型比二次函数模型更好
温度x/ 21 23 25 27
Z=lny 1.946 2.398 3.405 3.178
产卵数y/个 7 11 21 24
29 32 35
4.190 4.745 5.784
66 115 325
1)确定解释变量和预报变量;
2)画出散点图;
3)确定回归方程类型;
4)求出回归方程;
5)利用相关指数或残差进行分析.
对两个分类变量的相关关系的分析方法:
①通过图形直观判断两个分类变量是否相关;
②独立性检验.
由列联表可以粗略估计出,在不吸烟者中,有0.54%患有肺癌;在吸烟者中,有2.28%患有肺癌。因此,直观上可以得到结论:吸烟者和不吸烟者患肺癌的可能性存在差异.
为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人):
吸烟与患肺癌列联表:
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
1、列联表
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
2、等高条形图
等高条形图更清晰地表达了两种情况下患肺癌的比例.
独立性检验:
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
为了使不同样本容量的数据有统一的评判标准,我们构造一个随机变量
由列联表中数据,利用公式(1)计算得K2的观测值为:
(1)
其中n=a+b+c+d为样本容量.
我们在犯错误概率不超过0.01的前提下,认为“吸烟与患肺癌有关系”.
(1)如果k>10.828,就有99.9%的把握认为“X与Y有关系”;
(2)如果k>6.635,就有99%的把握认为“X与Y有关系”;
(3)如果k>2.706,就有90%的把握认为“X与Y有关系”;
(4)如果k<=2.706,就认为没有充分的证据显示
“X与Y有关系”.
临界值
例2 为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中随机抽取60名学生,得到如下列联表:
在多大程度上可以认为高中生的性别与是否喜欢数学课程之间有关系?为什么?
喜欢数学课程 不喜欢数学课程 总计
男 24 16 40
女 15 5 20
总计 39 21 60
计算得K2的观测值为:
我们有99%的把握认为高中生的性别与是否喜欢数学课程之间有关系。
课堂小结:
一:回归分析的基本思想和应用
二:独立性检验的基本思想和应用
练习:
作业:习题1.2
