3.2.2 复数代数形式的乘除运算 课件 31张PPT
文档属性
| 名称 | 3.2.2 复数代数形式的乘除运算 课件 31张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 21:09:28 | ||
图片预览











文档简介
(共31张PPT)
3.2.2
回顾旧知
复数加减法的运算法则是什么?
两个复数相加(减)就是实部与实部,虚部与虚部分别相加(减).
复数加法和减法运算的几何意义是什么?
复数的加、减法可以按照向量的加、减法来进行.
实数能进行加、减、乘、除运算,那么复数呢?
新课导入
其实,复数除了可以相加相减之外,它还可以乘除呢!这也是我们这节课的重点.
进入我们今天学习的内容.
学习目标
1.理解复数代数形式的四则运算,并能用运算律进行
复数的四则运算。
2.能根据所给的运算形式选择恰当的方法进行四则运算。
3.掌握类比的数学方法。
多项式的乘法运算 ?
(a+b)(c+d)=ac+ad+bc+bd
由多项式的乘法法则,我们可以类比出复数的乘法法则吗?
我们规定,复数的乘法法则如下:
能描述出复数乘法的运算法则吗?
设z1=a+bi, z2=c+di 是任意两个复数,那么它们的积
复数的乘法是否满足交换律、结合律?乘法对加法满足分配律吗?
思考…
计算 (1-2i)(3+4i)(-2+i)
复数的乘法与多项式的乘法是类似的,我们知道多项式的乘法用乘法公式可迅速展开, 运算,类似地,复数的乘法也可大胆运用乘法公式来展开运算.
解: 原式=(11-2i)(-2+i)
=-20+15i.
(-2i)4i=8
而不是
-8!
本例可以用复数的乘法法则计算,也可以用乘法公式计算.
实数系中的乘法公式在复数系中也是成立的.
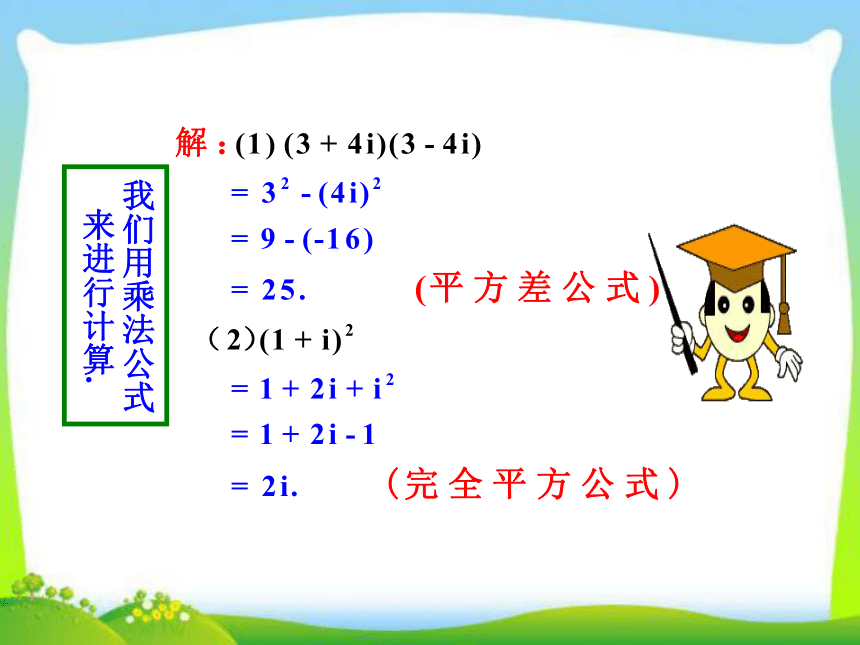
我们用乘法公式来进行计算.
我们把这两个复数3+4i,3-4i称为共轭复数.
注意本例 (1) 3+4i 与 3-4i 两复数的特点.
一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.虚部不等于0的两个共轭复数也叫做共轭虚数.
若Z1,Z2,是共轭复数,那么
(1)在复平面内,它们所对应的点有怎样的位置关系?
( )
(2)Z1Z2是一个怎样的数?( )
复数z=a+bi的共轭复数记作
动动脑
关于X轴对称
实数
类比实数的除法是乘法的逆运算,我们规定复数的除法是乘法的逆运算,试探求复数除法的法则.
做根式除法时,分子分母都乘以分母的“有理化因式”,从而使分母“有理化”.
我们可以类比根式的除法,从而得到简便的操作方法:先把两个复数相除写成分数形式,然后把分子与分母都乘以分母的共轭复数,使分母“实数化”,最后在化简.
大家想想我们如何处理根式除法的?
用上面的方法把分母“实数化”.
课堂小结
设z1=a+bi, z2=c+di 是任意两个复数,那么它们的积
1.复数的乘法法则如下:
3.两个复数的积是一个确定的复数.
2.复数的乘法与多项式的乘法是类似的,复数的乘法也可运用乘法公式来展开运算.
4.复数的乘法仍然满足交换律、结合律、分配律.
6.复数z=a+bi的共轭复数记作
5.一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.
7.复数的除法是乘法的逆运算.
8.复数的除法法则:
9.在实际中我们进行复数相除的方法是:先把两个复数相除写成分数形式,然后把分子与分母都乘以分母的共轭复数,使分母“实数化”,最后在化简.
高考链接
答案:C.
(17.全国1)下列运算结果为纯虚数的是()
随堂练习
填空
-3-i
-3+4i
.
选择
D
D
解答题
X=-3
2.
3.计算
解:
习题答案
练习(第111页)
1. (1) -18-21i; (2) 6-17i; (3) -20-15i.
2. (1) -5; (2) -2i; (3) 5.
3. (1) i; (2) -i; (3) 1-I; (4) -1-3i.
3.2.2
回顾旧知
复数加减法的运算法则是什么?
两个复数相加(减)就是实部与实部,虚部与虚部分别相加(减).
复数加法和减法运算的几何意义是什么?
复数的加、减法可以按照向量的加、减法来进行.
实数能进行加、减、乘、除运算,那么复数呢?
新课导入
其实,复数除了可以相加相减之外,它还可以乘除呢!这也是我们这节课的重点.
进入我们今天学习的内容.
学习目标
1.理解复数代数形式的四则运算,并能用运算律进行
复数的四则运算。
2.能根据所给的运算形式选择恰当的方法进行四则运算。
3.掌握类比的数学方法。
多项式的乘法运算 ?
(a+b)(c+d)=ac+ad+bc+bd
由多项式的乘法法则,我们可以类比出复数的乘法法则吗?
我们规定,复数的乘法法则如下:
能描述出复数乘法的运算法则吗?
设z1=a+bi, z2=c+di 是任意两个复数,那么它们的积
复数的乘法是否满足交换律、结合律?乘法对加法满足分配律吗?
思考…
计算 (1-2i)(3+4i)(-2+i)
复数的乘法与多项式的乘法是类似的,我们知道多项式的乘法用乘法公式可迅速展开, 运算,类似地,复数的乘法也可大胆运用乘法公式来展开运算.
解: 原式=(11-2i)(-2+i)
=-20+15i.
(-2i)4i=8
而不是
-8!
本例可以用复数的乘法法则计算,也可以用乘法公式计算.
实数系中的乘法公式在复数系中也是成立的.
我们用乘法公式来进行计算.
我们把这两个复数3+4i,3-4i称为共轭复数.
注意本例 (1) 3+4i 与 3-4i 两复数的特点.
一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.虚部不等于0的两个共轭复数也叫做共轭虚数.
若Z1,Z2,是共轭复数,那么
(1)在复平面内,它们所对应的点有怎样的位置关系?
( )
(2)Z1Z2是一个怎样的数?( )
复数z=a+bi的共轭复数记作
动动脑
关于X轴对称
实数
类比实数的除法是乘法的逆运算,我们规定复数的除法是乘法的逆运算,试探求复数除法的法则.
做根式除法时,分子分母都乘以分母的“有理化因式”,从而使分母“有理化”.
我们可以类比根式的除法,从而得到简便的操作方法:先把两个复数相除写成分数形式,然后把分子与分母都乘以分母的共轭复数,使分母“实数化”,最后在化简.
大家想想我们如何处理根式除法的?
用上面的方法把分母“实数化”.
课堂小结
设z1=a+bi, z2=c+di 是任意两个复数,那么它们的积
1.复数的乘法法则如下:
3.两个复数的积是一个确定的复数.
2.复数的乘法与多项式的乘法是类似的,复数的乘法也可运用乘法公式来展开运算.
4.复数的乘法仍然满足交换律、结合律、分配律.
6.复数z=a+bi的共轭复数记作
5.一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.
7.复数的除法是乘法的逆运算.
8.复数的除法法则:
9.在实际中我们进行复数相除的方法是:先把两个复数相除写成分数形式,然后把分子与分母都乘以分母的共轭复数,使分母“实数化”,最后在化简.
高考链接
答案:C.
(17.全国1)下列运算结果为纯虚数的是()
随堂练习
填空
-3-i
-3+4i
.
选择
D
D
解答题
X=-3
2.
3.计算
解:
习题答案
练习(第111页)
1. (1) -18-21i; (2) 6-17i; (3) -20-15i.
2. (1) -5; (2) -2i; (3) 5.
3. (1) i; (2) -i; (3) 1-I; (4) -1-3i.
