3.2复数代数形式的乘除运算 课件 18张PPT
文档属性
| 名称 | 3.2复数代数形式的乘除运算 课件 18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 493.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 21:12:34 | ||
图片预览





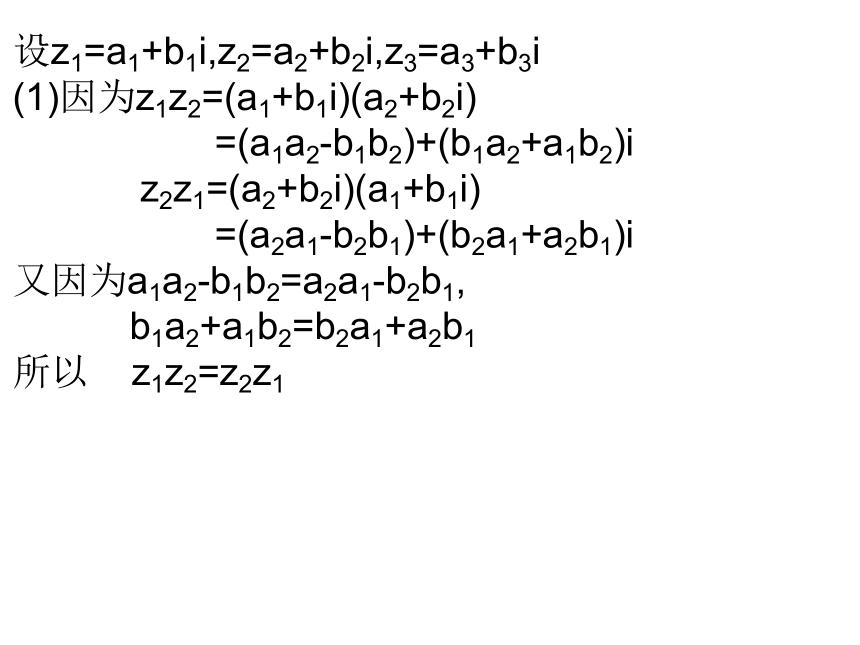

文档简介
(共18张PPT)
设复数z1=a+bi,z2=c+di,则 z1+z2,z1-z2分别等于什么?
z1+z2=(a+c)+(b+d)i.
z1-z2=(a-c)+(b-d)i
复习巩固
1、设a,b,c,d∈R,则(a+b)(c+d)怎样展开?
(a+b)(c+d)=ac+ad+bc+bd
问题探究
设复数z1=a+bi,z2=c+di,其中a,b,c,d∈R,则z1z2=(a+bi)(c+di),按照上述运算法则将其展开,z1z2等于什么?
z1z2=(ac-bd)+(ad+bc)i.
形成结论
复数乘法的法则
两个复数相乘所得结果还是一个复数
2、复数的乘法是否满足交换律、结合律和对加法的分配律?
交换律: z1·z2=z2·z1
结合律:(z1·z2)·z3=z1·(z2·z3)
分配率: z1(z2+z3)=z1z2+z1z3
问题探究
设z1=a1+b1i,z2=a2+b2i,z3=a3+b3i
(1)因为z1z2=(a1+b1i)(a2+b2i)
=(a1a2-b1b2)+(b1a2+a1b2)i
z2z1=(a2+b2i)(a1+b1i)
=(a2a1-b2b1)+(b2a1+a2b1)i
又因为a1a2-b1b2=a2a1-b2b1,
b1a2+a1b2=b2a1+a2b1
所以 z1z2=z2z1
设z1=a1+b1i,z2=a2+b2i,z3=a3+b3i
(2)因为(z1z2)z3
=[(a1+b1i)(a2+b2i)](a3+b3i)
=[(a1a2-b1b2)a3-(b1a2+a1b2)b3]
+[(b1a2+a1b2)a3+(a1a2-b1b2)b3]i
=(a1a2a3-b1b2a3-b1a2b3-a1b2b3)
+(b1a2a3+a1b2a3+a1a2b3-b1b2b3)i
同理可得z1(z2z3)
=(a1a2a3-b1b2a3-b1a2b3-a1b2b3)
+(b1a2a3+a1b2a3+a1a2b3-b1b2b3)i
所以 (z1z2)z3=z1(z2z3)
设z1=a1+b1i,z2=a2+b2i,z3=a3+b3i
(3)因为z1(z2+z3)=(a1+b1i)[(a2+b2i)+(a3+b3i)]
=(a1+b1i)[(a2+a3)+(b2+b1)i]
=[a1(a2+a3)-b1(b2+b3)]+[b1(a2+a3)+a1(b2+b3)]i
=(a1a2+a1a3-b1b2-b1b3)
+(b1a2+b1a3+a1b2+a1b3)i
z1z2+z1z3=(a1+b1i)(a2+b2i)+(a1+b1i)(a3+b3i)
=(a1a2 -b1b2)+(b1a2+a1b2)i
+(a1a3-b1b3)+(b1a3+a1b3)i
=(a1a2-b1b2+a1a3-b1b3)
+(b1a2+a1b2+b1a3+a1b3)i
=(a1a2+a1a3-b1b2-b1b3)
+(b1a2+b1a3+a1b2+a1b3)i
所以 z1(z2+z3)=z1z2+z1z3
例题讲解
例1:复数i(2-i)= ( )
A 1+2i
B 1-2i
C -1+2i
D -1-2i
解析:i(2-i)=2i-i2=1+2i
A
例题讲解
例2:计算 (1)(1+i)(1-i)-(1+i)2;
(2)(1+2i)(3+4i)(5+6i)-4i
解:(1)(1+i)(1-i)-(1+i)2=1-i2-2i=2-2i
(2)(1+2i)(3+4i)(5+6i)-4i
=(3+4i+6i+8i2)(5+6i)-4i
=(-5+10i)(5+6i)-4i
=-25-30i+50i+60i2-4i
=-85+16i
实部相等,虚部互为相反数的两个复数叫做互为共轭复数.
3、在实数中, 与 互称为有理化因式,在复数中,a+bi 与a-bi互称为共轭复数,一般地,共 轭复数的定义是什么?
问题探究
4、复数z的共轭复数记作 ,虚部不为零的两个共轭复数也叫做共轭虚数,那么z与 在复平面内所对应的点的位置关系如何? 等于什么?
关于实轴对称
问题探究
5、若复数z1=z2·z,则称复数z为复数z1除以z2所得的商,即z=z1÷z2. 一般地,设复数z1=a+bi,z2=c+di(c+di≠0),如何求z1÷z2?
问题探究
复数除法法则
形成结论
两个复数相除所得结果还是一个复数
例题讲解
例3:若复数z=i(3-2i),则 ( )
A 2-3i B 2+3i C 3+2i D 3-2i
解析:因为z=i(3-2i)=3i-2i2=2+3i,所以
A
例题讲解
例4:设复数z满足(1-i)z=2i,则z=( )
A -1+i B -1-i C 1+i D 1-i
解析:由题意,得
A
1.复数的乘法法则类似于两个多项式相乘,展开后要把i2换成-1,并将实部与虚部分别合并.若求几个复数的连乘积,则可利用交换律和结合律每次两两相乘.
2.复数的除法法则类似于两个根式的除法运算,一般先将除法运算式写成分式,再将分子分母同乘以分母的共轭复数,使分母化为实数,分子按乘法法则运算.
3.对复数的乘法、除法运算要求掌握它们的算法,不要求记忆运算公式,对复数式的运算结果,一般要化为代数式.
课堂小结
P61习题A组:4、5
布置作业
设复数z1=a+bi,z2=c+di,则 z1+z2,z1-z2分别等于什么?
z1+z2=(a+c)+(b+d)i.
z1-z2=(a-c)+(b-d)i
复习巩固
1、设a,b,c,d∈R,则(a+b)(c+d)怎样展开?
(a+b)(c+d)=ac+ad+bc+bd
问题探究
设复数z1=a+bi,z2=c+di,其中a,b,c,d∈R,则z1z2=(a+bi)(c+di),按照上述运算法则将其展开,z1z2等于什么?
z1z2=(ac-bd)+(ad+bc)i.
形成结论
复数乘法的法则
两个复数相乘所得结果还是一个复数
2、复数的乘法是否满足交换律、结合律和对加法的分配律?
交换律: z1·z2=z2·z1
结合律:(z1·z2)·z3=z1·(z2·z3)
分配率: z1(z2+z3)=z1z2+z1z3
问题探究
设z1=a1+b1i,z2=a2+b2i,z3=a3+b3i
(1)因为z1z2=(a1+b1i)(a2+b2i)
=(a1a2-b1b2)+(b1a2+a1b2)i
z2z1=(a2+b2i)(a1+b1i)
=(a2a1-b2b1)+(b2a1+a2b1)i
又因为a1a2-b1b2=a2a1-b2b1,
b1a2+a1b2=b2a1+a2b1
所以 z1z2=z2z1
设z1=a1+b1i,z2=a2+b2i,z3=a3+b3i
(2)因为(z1z2)z3
=[(a1+b1i)(a2+b2i)](a3+b3i)
=[(a1a2-b1b2)a3-(b1a2+a1b2)b3]
+[(b1a2+a1b2)a3+(a1a2-b1b2)b3]i
=(a1a2a3-b1b2a3-b1a2b3-a1b2b3)
+(b1a2a3+a1b2a3+a1a2b3-b1b2b3)i
同理可得z1(z2z3)
=(a1a2a3-b1b2a3-b1a2b3-a1b2b3)
+(b1a2a3+a1b2a3+a1a2b3-b1b2b3)i
所以 (z1z2)z3=z1(z2z3)
设z1=a1+b1i,z2=a2+b2i,z3=a3+b3i
(3)因为z1(z2+z3)=(a1+b1i)[(a2+b2i)+(a3+b3i)]
=(a1+b1i)[(a2+a3)+(b2+b1)i]
=[a1(a2+a3)-b1(b2+b3)]+[b1(a2+a3)+a1(b2+b3)]i
=(a1a2+a1a3-b1b2-b1b3)
+(b1a2+b1a3+a1b2+a1b3)i
z1z2+z1z3=(a1+b1i)(a2+b2i)+(a1+b1i)(a3+b3i)
=(a1a2 -b1b2)+(b1a2+a1b2)i
+(a1a3-b1b3)+(b1a3+a1b3)i
=(a1a2-b1b2+a1a3-b1b3)
+(b1a2+a1b2+b1a3+a1b3)i
=(a1a2+a1a3-b1b2-b1b3)
+(b1a2+b1a3+a1b2+a1b3)i
所以 z1(z2+z3)=z1z2+z1z3
例题讲解
例1:复数i(2-i)= ( )
A 1+2i
B 1-2i
C -1+2i
D -1-2i
解析:i(2-i)=2i-i2=1+2i
A
例题讲解
例2:计算 (1)(1+i)(1-i)-(1+i)2;
(2)(1+2i)(3+4i)(5+6i)-4i
解:(1)(1+i)(1-i)-(1+i)2=1-i2-2i=2-2i
(2)(1+2i)(3+4i)(5+6i)-4i
=(3+4i+6i+8i2)(5+6i)-4i
=(-5+10i)(5+6i)-4i
=-25-30i+50i+60i2-4i
=-85+16i
实部相等,虚部互为相反数的两个复数叫做互为共轭复数.
3、在实数中, 与 互称为有理化因式,在复数中,a+bi 与a-bi互称为共轭复数,一般地,共 轭复数的定义是什么?
问题探究
4、复数z的共轭复数记作 ,虚部不为零的两个共轭复数也叫做共轭虚数,那么z与 在复平面内所对应的点的位置关系如何? 等于什么?
关于实轴对称
问题探究
5、若复数z1=z2·z,则称复数z为复数z1除以z2所得的商,即z=z1÷z2. 一般地,设复数z1=a+bi,z2=c+di(c+di≠0),如何求z1÷z2?
问题探究
复数除法法则
形成结论
两个复数相除所得结果还是一个复数
例题讲解
例3:若复数z=i(3-2i),则 ( )
A 2-3i B 2+3i C 3+2i D 3-2i
解析:因为z=i(3-2i)=3i-2i2=2+3i,所以
A
例题讲解
例4:设复数z满足(1-i)z=2i,则z=( )
A -1+i B -1-i C 1+i D 1-i
解析:由题意,得
A
1.复数的乘法法则类似于两个多项式相乘,展开后要把i2换成-1,并将实部与虚部分别合并.若求几个复数的连乘积,则可利用交换律和结合律每次两两相乘.
2.复数的除法法则类似于两个根式的除法运算,一般先将除法运算式写成分式,再将分子分母同乘以分母的共轭复数,使分母化为实数,分子按乘法法则运算.
3.对复数的乘法、除法运算要求掌握它们的算法,不要求记忆运算公式,对复数式的运算结果,一般要化为代数式.
课堂小结
P61习题A组:4、5
布置作业
