选修1-2 第三章 数系的扩充与复数的引入复习参考题 课件 21张PPT
文档属性
| 名称 | 选修1-2 第三章 数系的扩充与复数的引入复习参考题 课件 21张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 446.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 21:27:18 | ||
图片预览







文档简介
(共21张PPT)
数系的扩充与复数的引入
复习参考题
高中数学人教A版2003课标版
选修1-2
课前热身练习
课本P63
A组第一题
双基目标
(1)了解引进复数的必要性,了解数集的扩充过程:自然数集(N)→整数集(Z)→有理数集(Q)→实数集(R)→复数集(C).
(2)理解在数系的扩充中由实数集扩展到复数集出现的一些基本概念.例如:虚数单位、复数、虚数、纯虚数、共轭复数、实部、虚部等等.理解复数相等的充要条件.
(3)了解复数的代数表示法及其几何意义.
(4)掌握复数代数形式的四则运算法则,了解复数代数形式的加法、减法运算的几何意义.了解在不同数集中运算法则的联系和区别.
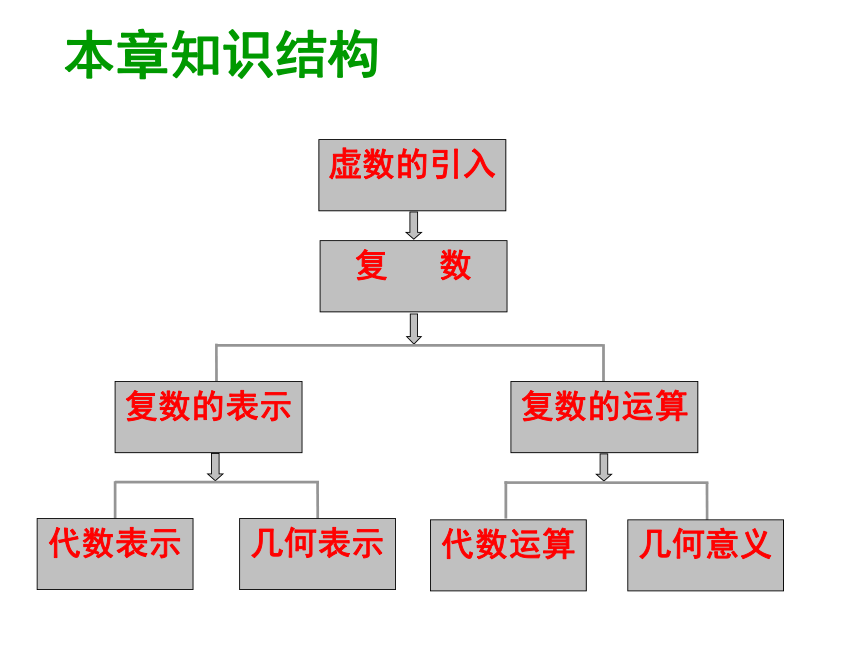
本章知识结构
一、基础回顾
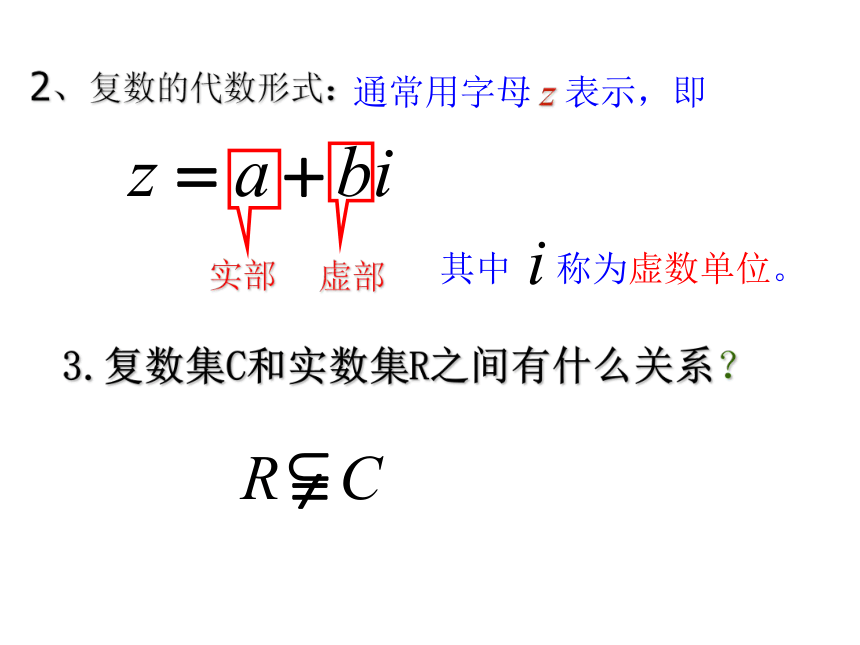
实部 虚部
2、复数的代数形式:
3.复数集C和实数集R之间有什么关系?
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
x轴------实轴
y轴------虚轴
(数)
(形)
一一对应
5、复数的一个几何意义
三、复数的运算法则
例1、下列命题中,正确命题的个数是 ( )
①若x,y∈C则x+yi=1+i的充要条件是x=y=1;
②若a,b∈R且a>b,则a+i>b+i;
③若x2+y2=0,则x=y=0.
A.0 B.1 C.2 D.3
[分析] 由题目可获取以下主要信息:
①题中给出了三个命题;
②判断正确命题的个数.
解答本题只需根据复数的有关概念判断即可.
[答案] A
[解析] ①由于x,y∈C,所以x+yi不一定是复数的代数形式,不符合复数相等的充要条件,①是假命题.
②由于两个虚数不能比较大小,
∴②是假命题.
③当x=1,y=i时
x2+y2=0成立,∴③是假命题.
例3、解答题
实数m分别取什么数值时,复数z=(m2+5m+6)+(m2-2m-15)i是:
(1)实数;
(2)虚数;
(3)纯虚数.
思路点拨:化简z为代数形式,确定其实部、虚部。
所以z对应的点位于第一象限
【题后感悟】复数与复平面内的点是一一对应的,复数和复
平面内以原点为起点的向量也是一一对应的,因此复数加、
减法的几何意义可按平面向量加、减法理解,利用平行四边
形法则或三角形法则解决问题。
A.第一象限 B.第二象限
C.第三象限 D.第四象限
例4、
例例例例55
【题后感悟】复数的加法、减法运算可以类比多项式运算,
除法关键是分子、分母同乘以分母的共轭复数,注意要把i
的幂写成最简形式
-2i
1、复数代数运算的实质是转化为实数运算,在转化时常用
的知识有复数相等,复数的加、减、乘、除运算法则,模的性质,共轭复数的性质等。
2、解决复数问题两个基本途径:①利用复数相等转化为实数问题,②利用复数的几何表示(点、向量)数形结合去解决.
●课时小结
【课后作业】
老师整理出来的近几年年全国各省市关于复数内容的高考真题.
课堂练习
B组2
课外作业p63 2. 3 题
拓展练习
例6、满足条件|z-i|=|3+4i|的复数z在复平面上的对应点的轨迹是 ( )
A.一条直线 B.两条直线
C.圆 D.椭圆
[答案] C
数系的扩充与复数的引入
复习参考题
高中数学人教A版2003课标版
选修1-2
课前热身练习
课本P63
A组第一题
双基目标
(1)了解引进复数的必要性,了解数集的扩充过程:自然数集(N)→整数集(Z)→有理数集(Q)→实数集(R)→复数集(C).
(2)理解在数系的扩充中由实数集扩展到复数集出现的一些基本概念.例如:虚数单位、复数、虚数、纯虚数、共轭复数、实部、虚部等等.理解复数相等的充要条件.
(3)了解复数的代数表示法及其几何意义.
(4)掌握复数代数形式的四则运算法则,了解复数代数形式的加法、减法运算的几何意义.了解在不同数集中运算法则的联系和区别.
本章知识结构
一、基础回顾
实部 虚部
2、复数的代数形式:
3.复数集C和实数集R之间有什么关系?
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
x轴------实轴
y轴------虚轴
(数)
(形)
一一对应
5、复数的一个几何意义
三、复数的运算法则
例1、下列命题中,正确命题的个数是 ( )
①若x,y∈C则x+yi=1+i的充要条件是x=y=1;
②若a,b∈R且a>b,则a+i>b+i;
③若x2+y2=0,则x=y=0.
A.0 B.1 C.2 D.3
[分析] 由题目可获取以下主要信息:
①题中给出了三个命题;
②判断正确命题的个数.
解答本题只需根据复数的有关概念判断即可.
[答案] A
[解析] ①由于x,y∈C,所以x+yi不一定是复数的代数形式,不符合复数相等的充要条件,①是假命题.
②由于两个虚数不能比较大小,
∴②是假命题.
③当x=1,y=i时
x2+y2=0成立,∴③是假命题.
例3、解答题
实数m分别取什么数值时,复数z=(m2+5m+6)+(m2-2m-15)i是:
(1)实数;
(2)虚数;
(3)纯虚数.
思路点拨:化简z为代数形式,确定其实部、虚部。
所以z对应的点位于第一象限
【题后感悟】复数与复平面内的点是一一对应的,复数和复
平面内以原点为起点的向量也是一一对应的,因此复数加、
减法的几何意义可按平面向量加、减法理解,利用平行四边
形法则或三角形法则解决问题。
A.第一象限 B.第二象限
C.第三象限 D.第四象限
例4、
例例例例55
【题后感悟】复数的加法、减法运算可以类比多项式运算,
除法关键是分子、分母同乘以分母的共轭复数,注意要把i
的幂写成最简形式
-2i
1、复数代数运算的实质是转化为实数运算,在转化时常用
的知识有复数相等,复数的加、减、乘、除运算法则,模的性质,共轭复数的性质等。
2、解决复数问题两个基本途径:①利用复数相等转化为实数问题,②利用复数的几何表示(点、向量)数形结合去解决.
●课时小结
【课后作业】
老师整理出来的近几年年全国各省市关于复数内容的高考真题.
课堂练习
B组2
课外作业p63 2. 3 题
拓展练习
例6、满足条件|z-i|=|3+4i|的复数z在复平面上的对应点的轨迹是 ( )
A.一条直线 B.两条直线
C.圆 D.椭圆
[答案] C
