人教版数学八年级下册17.1《勾股定理》 课件(共29张PPT)
文档属性
| 名称 | 人教版数学八年级下册17.1《勾股定理》 课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 07:58:40 | ||
图片预览





文档简介
(共29张PPT)
17.1 勾股定理的认识
新课标人民教育出版社
八年级数学(下册)
是否有外星人存在呢?如果有的话,我们怎么样才能与”外星人”接触呢?
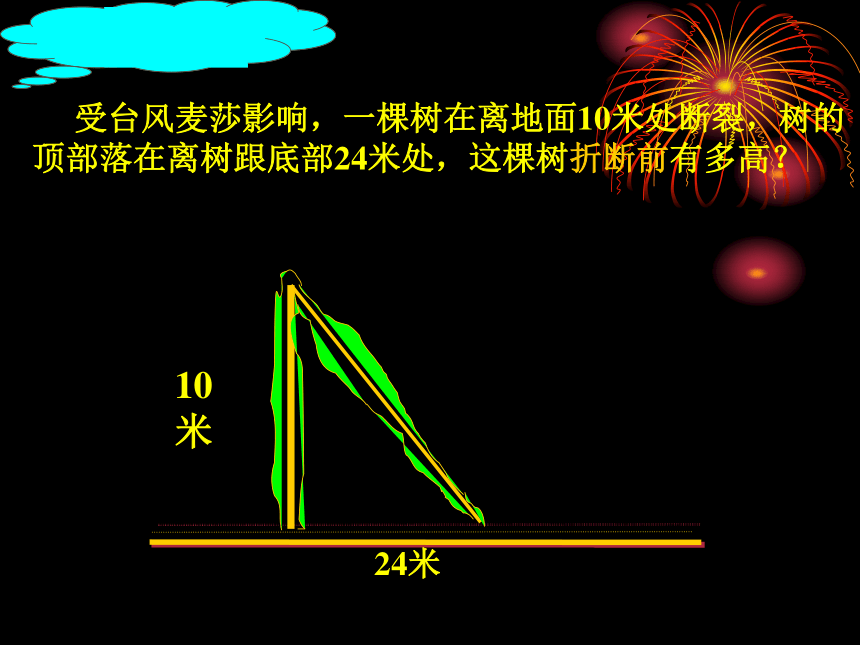
受台风麦莎影响,一棵树在离地面10米处断裂,树的
顶部落在离树跟底部24米处,这棵树折断前有多高?
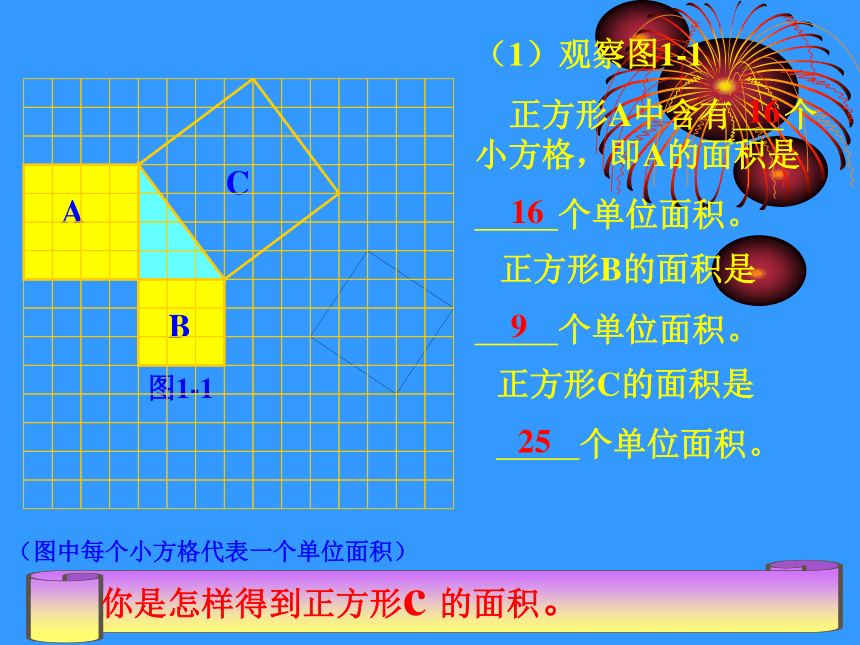
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
16
16
9
25
(图中每个小方格代表一个单位面积)
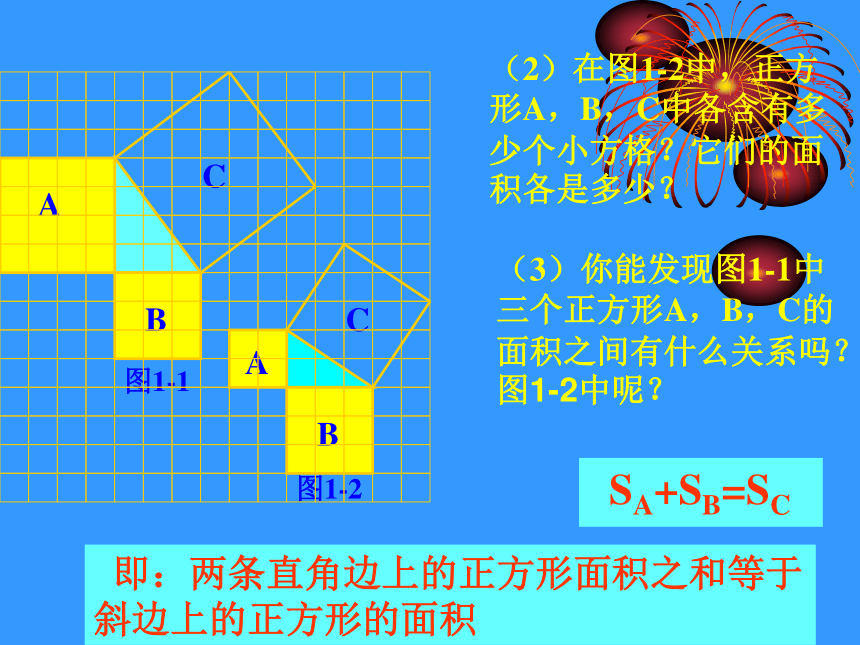
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?图1-2中呢?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
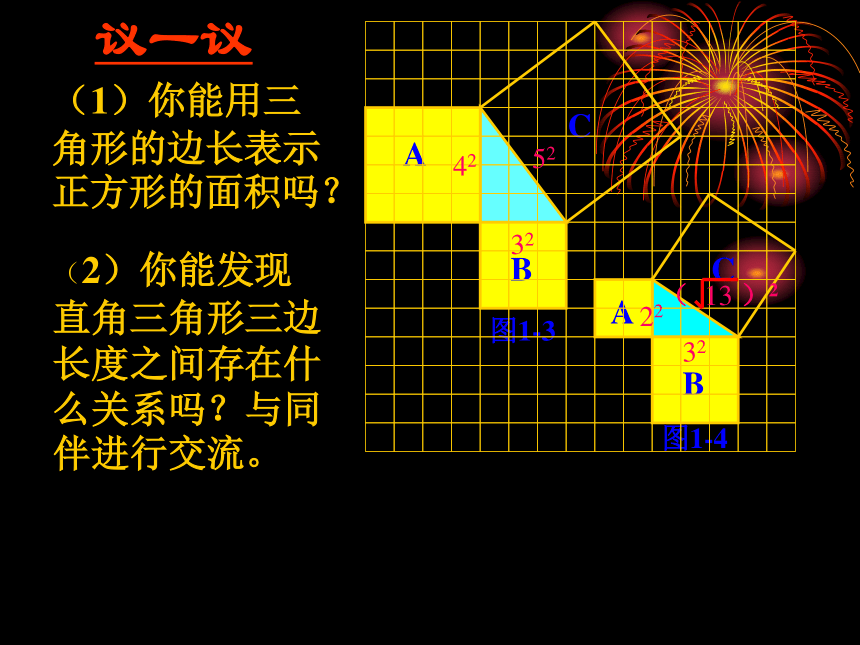
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
议一议
42
32
52
22
32
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
结论变形
直角三角形中,两直角边的平方和等于斜边的平方;
c2=a2 + b2
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
千古第一定理
数与形的第一定理
导致第一次数学危机
数学由计算转变为证明
是第一个不定方程
毕
达
哥
拉
斯
定
理
勾股(商高)定理
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。
有趣的总统证法
无字证明
青出
a
b
c
无字证明
青出
青朱出入图
无字证明
读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
图1-1
图1-2
2002年国际数学家大会会标
1、求下列用字母表示的边长
应用知识回归生活
2、直角三角形中两条直角边之比为3:4,且斜边为10cm,求(1)两直角边的长(2)斜边上的高线长
应用知识回归生活
5:在电线杆离地面8米高的地方向地面拉一条长10米的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方?
4、如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离
40
应用知识回归生活
在平静的湖面上,有一支红莲,高出水面1尺红莲被风一吹,花朵刚好与水面平齐,已知红莲移动的水平距离是2尺问这里水深是多少?
应用知识回归生活
思考题
探索勾股定理
想一想
我们有:
好奇是人的本性!
46
b=58
a=46
58
c
c2=a2+b2 =462+582
=5480
而742=5476
由勾股定理得:
在误差范围内
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度
课后探索
做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒊勾股定理的主要作用是 在直角三角形中,已知任意两边求第三边的长
美丽的勾股树
再见!
17.1 勾股定理的认识
新课标人民教育出版社
八年级数学(下册)
是否有外星人存在呢?如果有的话,我们怎么样才能与”外星人”接触呢?
受台风麦莎影响,一棵树在离地面10米处断裂,树的
顶部落在离树跟底部24米处,这棵树折断前有多高?
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
16
16
9
25
(图中每个小方格代表一个单位面积)
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?图1-2中呢?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
议一议
42
32
52
22
32
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
结论变形
直角三角形中,两直角边的平方和等于斜边的平方;
c2=a2 + b2
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
千古第一定理
数与形的第一定理
导致第一次数学危机
数学由计算转变为证明
是第一个不定方程
毕
达
哥
拉
斯
定
理
勾股(商高)定理
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。
有趣的总统证法
无字证明
青出
a
b
c
无字证明
青出
青朱出入图
无字证明
读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
图1-1
图1-2
2002年国际数学家大会会标
1、求下列用字母表示的边长
应用知识回归生活
2、直角三角形中两条直角边之比为3:4,且斜边为10cm,求(1)两直角边的长(2)斜边上的高线长
应用知识回归生活
5:在电线杆离地面8米高的地方向地面拉一条长10米的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方?
4、如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离
40
应用知识回归生活
在平静的湖面上,有一支红莲,高出水面1尺红莲被风一吹,花朵刚好与水面平齐,已知红莲移动的水平距离是2尺问这里水深是多少?
应用知识回归生活
思考题
探索勾股定理
想一想
我们有:
好奇是人的本性!
46
b=58
a=46
58
c
c2=a2+b2 =462+582
=5480
而742=5476
由勾股定理得:
在误差范围内
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度
课后探索
做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒊勾股定理的主要作用是 在直角三角形中,已知任意两边求第三边的长
美丽的勾股树
再见!
