2019-2020学年山东省菏泽市郓城县七年级(上)期末数学试卷(解析版)
文档属性
| 名称 | 2019-2020学年山东省菏泽市郓城县七年级(上)期末数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 339.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 07:20:31 | ||
图片预览

文档简介
2019-2020学年山东省菏泽市郓城县七年级(上)期末数学试卷
一、选择题(每小题给出的四个选项中,只有一个是正确的,把正确选项的代号填入该小题后的括号内,每小题3分,共24分)
1.(3分)如图,长方体的底面是长为4cm、宽为2cm的长方形,如果从左面看这个长方体时看到的图形面积为6cm2,则这个长方体的体积等于( )
A.6cm3 B.8cm3 C.12cm3 D.24cm3
2.(3分)将一把刻度尺按如图所示放在数轴上(数轴的单位长度是1cm),刻度尺上的“0cm”和“8cm”分别对应数轴上的﹣3.6和x,则x的值为( )
A.4.2 B.4.3 C.4.4 D.4.5
3.(3分)按如图的运算程序,能使输出结果为3的x,y的值是( )
A.x=5,y=﹣2 B.x=3,y=﹣3 C.x=﹣4,y=2 D.x=﹣3,y=﹣9
4.(3分)如图,从A地到B地的最短路线是( )
A.A→F→E→B B.A→C→E→B C.A→D→G→E→B D.A→G→E→B
5.(3分)在海上有两艘军舰A和B,测得A在B的北偏西60°方向上,则由A测得B的方向是( )
A.南偏东30° B.南偏东60° C.北偏西30° D.北偏西60°
6.(3分)下列方程中,是一元一次方程的是( )
A.x2﹣4x=3 B. C.x+2y=1 D.xy﹣3=5
7.(3分)某种商品因换季准备打折出售,如果按原定价的七五折出售,将赔25元,而按原定价的九折出售,将赚20元,则这种商品的原价是( )
A.500元 B.400元 C.300元 D.200元
8.(3分)为了了解某校九年级学生的体能情况,随机抽查了该校九年级若干名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的直方图,请根据图示计算,仰卧起坐次数在25~30次的学生人数占被调查学生人数的百分比为( )
A.40% B.30% C.20% D.10%
二、填空题(每小题3分,共18分)
9.(3分)点A,B在数轴上的位置如图所示,点C是数轴上的一点,且BC=AB,则点C对应的有理数是 .
10.(3分)如图,将小王某月手机费中各项费用的情况制成扇形统计图,表示短信费的扇形的圆心角等于 度.
11.(3分)下列方程:①x+2=0;②4x=8;③=3.其中解为x=2的是 (填序号).
12.(3分)在有理数范围内定义一种新运算“⊕”,其运算规则为:a⊕b=﹣2a+3b,如1⊕5=﹣2×1+3×5=13,则方程2x⊕4=0的解为 .
13.(3分)如今,中学生睡眠不足的问题正愈演愈烈,“缺觉”已是全国中学生们的老大难问题.教育部规定,初中生每天的睡眠时间应为9个小时.鹏鹏记录了他一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则鹏鹏这一周的睡眠够9个小时的有 天.
14.(3分)如图,整个圆表示某班参加课外活动的总人数,跳绳的人数占30%,表示踢毽的扇形圆心角是60°,踢毽和打篮球的人数比是1:2,那么表示参加“其它”活动的人数占总人数的 %.
三、解答题(共78分,解答要写出必要的文字说明、演算步骤)
15.(6分)如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
16.(6分)一辆货车从超市出发送货.先向南行驶30km到达A单位,继续向南行驶20km到达B单位.回到超市后,又给向北15km处的C单位送了3次货,然后回到超市休息.
(1)C单位离A单位有多远?
(2)该货车一共行驶了多少km?
17.(7分)一个花坛的形状如图所示,它的两端是半径相等的半圆,求:
(1)花坛的周长l;
(2)花坛的面积S;
(3)若a=8m,r=5m,求此时花坛的周长及面积(π取3.14).
18.(8分)已知点A,B如图所示,请你按照下列要求画图(延长线都画成虚线):
(1)过点A,B画直线AB,并在直线AB上方任取两点C,D;
(2)画射线AC,线段CD;
(3)延长线段CD,与直线AB相交于点M;
(4)画线段DB,反向延长线段DB,与射线AC相交于点N.
19.(8分)如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=50°,∠DOE=35°,那么∠BOD是多少度?
(2)如果∠AOE=160°,∠COD=40°,那么∠AOB是多少度?
20.(8分)根据以下对话,分别求小红所买的笔和笔记本的价格.
21.(8分)某服装厂要生产某种型号的学生校服,已知3m长的某种布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,库内存这种布料600m,应如何分配布料做上衣和做裤子才能恰好配套?共能做多少套?
22.(8分)某人为了解他所在地区的旅游情况,收集了该地区2014年到2017年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题:
(1)该地区2014年到2017年四年的年旅游平均收入是多少亿元;
(2)从折线统计图中你能获得哪些信息?
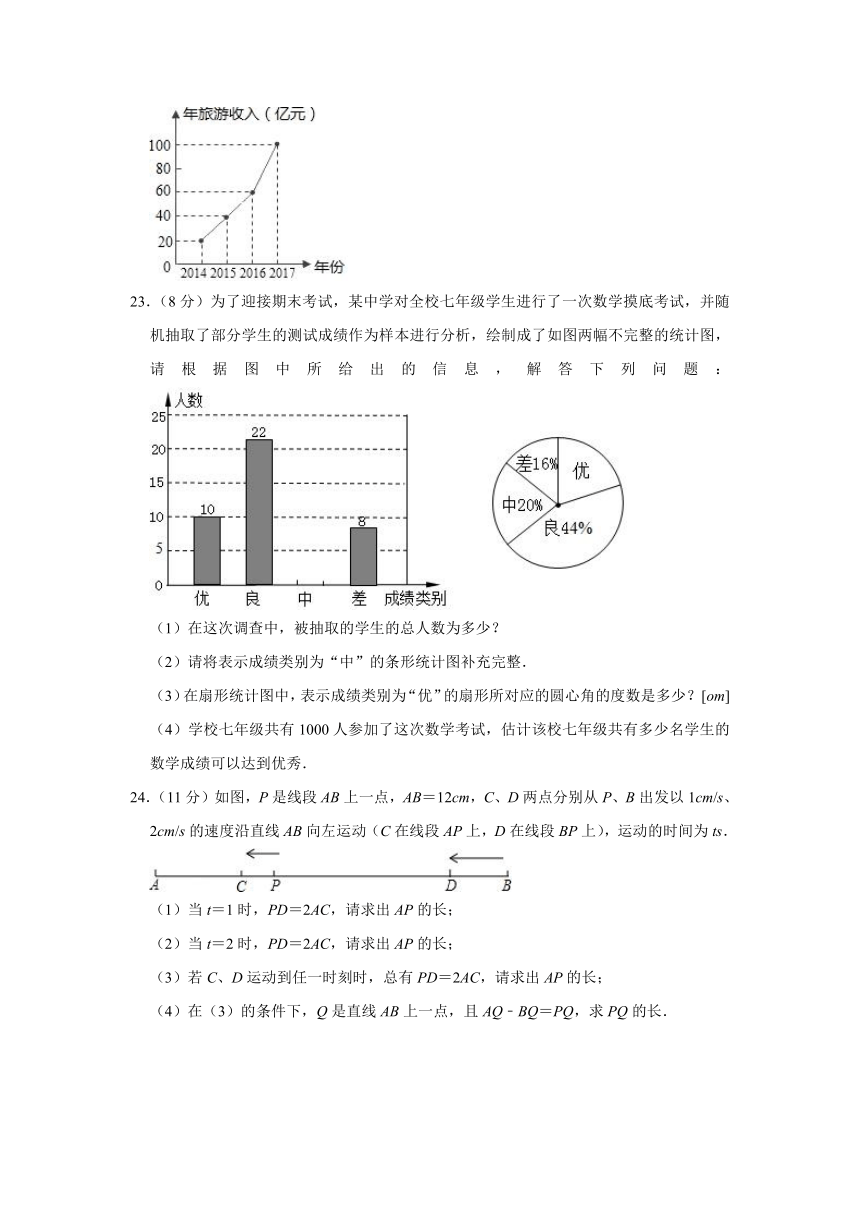
23.(8分)为了迎接期末考试,某中学对全校七年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如图两幅不完整的统计图,请根据图中所给出的信息,解答下列问题:
(1)在这次调查中,被抽取的学生的总人数为多少?
(2)请将表示成绩类别为“中”的条形统计图补充完整.
(3)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角的度数是多少?[om]
(4)学校七年级共有1000人参加了这次数学考试,估计该校七年级共有多少名学生的数学成绩可以达到优秀.
24.(11分)如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为ts.
(1)当t=1时,PD=2AC,请求出AP的长;
(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
2019-2020学年山东省菏泽市郓城县七年级(上)期末数学试卷
参考答案与试题解析
一、选择题(每小题给出的四个选项中,只有一个是正确的,把正确选项的代号填入该小题后的括号内,每小题3分,共24分)
1.(3分)如图,长方体的底面是长为4cm、宽为2cm的长方形,如果从左面看这个长方体时看到的图形面积为6cm2,则这个长方体的体积等于( )
A.6cm3 B.8cm3 C.12cm3 D.24cm3
【分析】直接利用长方体的左视图面积得出其高度,进而利用长方体体积求法得出答案.
【解答】解:∵从左面看这个长方体时看到的图形面积为6cm2,
∴这个长方体为:6÷2=3(cm),
∴这个长方体的体积等于:4×2×3=24(cm3).
故选:D.
2.(3分)将一把刻度尺按如图所示放在数轴上(数轴的单位长度是1cm),刻度尺上的“0cm”和“8cm”分别对应数轴上的﹣3.6和x,则x的值为( )
A.4.2 B.4.3 C.4.4 D.4.5
【分析】根据数轴得出算式x﹣(﹣3.6)=8﹣0,求出即可.
【解答】解:根据数轴可知:x﹣(﹣3.6)=8﹣0,
解得x=4.4.
故选:C.
3.(3分)按如图的运算程序,能使输出结果为3的x,y的值是( )
A.x=5,y=﹣2 B.x=3,y=﹣3 C.x=﹣4,y=2 D.x=﹣3,y=﹣9
【分析】根据运算程序列出方程,再根据二元一次方程的解的定义对各选项分析判断利用排除法求解.
【解答】解:由题意得,2x﹣y=3,
A、x=5时,y=7,故A选项错误;
B、x=3时,y=3,故B选项错误;
C、x=﹣4时,y=﹣11,故C选项错误;
D、x=﹣3时,y=﹣9,故D选项正确.
故选:D.
4.(3分)如图,从A地到B地的最短路线是( )
A.A→F→E→B B.A→C→E→B C.A→D→G→E→B D.A→G→E→B
【分析】此题为数学知识的应用,由题意从A地到B地,肯定要尽量缩短两地之间的里程,就用到两点间线段最短定理.
【解答】解:因为两点之间线段最短,从A地到B地,最短路线是最少走曲线,沿直线,行走即为A→F→E→B.
故选:A.
5.(3分)在海上有两艘军舰A和B,测得A在B的北偏西60°方向上,则由A测得B的方向是( )
A.南偏东30° B.南偏东60° C.北偏西30° D.北偏西60°
【分析】方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度.根据定义,正确画出图形,利用平行线的性质就可以解决.
【解答】解:如图:∵N1A∥N2B,∠2=60°,
∴∠1=∠2=60°,由方向角的概念可知由A测得B的方向是南偏东60°.
故选:B.
6.(3分)下列方程中,是一元一次方程的是( )
A.x2﹣4x=3 B. C.x+2y=1 D.xy﹣3=5
【分析】根据一元一次方程的定义:只含有一个未知数(元),且未知数的次数是1,这样的方程叫一元一次方程可得答案.
【解答】解:A、是一元二次方程,故此选项错误;
B、是一元一次方程,故此选项正确;
C、是二元一次方程,故此选项错误;
D、是二元二次方程,故此选项错误;
故选:B.
7.(3分)某种商品因换季准备打折出售,如果按原定价的七五折出售,将赔25元,而按原定价的九折出售,将赚20元,则这种商品的原价是( )
A.500元 B.400元 C.300元 D.200元
【分析】如果设这种商品的原价是x元,本题中唯一不变的是商品的成本,根据利润=售价﹣成本,即可列出方程求解.
【解答】解:设这种商品的原价是x元,根据题意得:75%x+25=90%x﹣20,
解得x=300.
故选:C.
8.(3分)为了了解某校九年级学生的体能情况,随机抽查了该校九年级若干名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的直方图,请根据图示计算,仰卧起坐次数在25~30次的学生人数占被调查学生人数的百分比为( )
A.40% B.30% C.20% D.10%
【分析】根据频率直方图可以知道被调查的总人数,又在要求的范围可以很直观地由图形看出,即可得出百分比.
【解答】解:由频率直方图可以得出,被调查的总人数=3+10+12+5=30.又仰卧起坐次数在25~30次的学生人数为12,故百分比为40%.
二、填空题(每小题3分,共18分)
9.(3分)点A,B在数轴上的位置如图所示,点C是数轴上的一点,且BC=AB,则点C对应的有理数是 2.5或5.5 .
【分析】根据数轴可得出点A表示的数是﹣2,点B表示的数是4,AB=4﹣(﹣2)=6,分两种情况可以得出答案.
【解答】解:由数轴可得出点A表示的数是﹣2,点B表示的数是4,AB=4﹣(﹣2)=6,分两种情况如下:
①点C在线段AB上,
因为BC=AB=×6=1.5,
所以点C对应的有理数是4﹣1.5=2.5;
②点C在线段AB的延长线上,
因为BC=AB=×6=1.5,
所以点C对应的有理数是4+1.5=5.5.
故答案为:2.5或5.5.
10.(3分)如图,将小王某月手机费中各项费用的情况制成扇形统计图,表示短信费的扇形的圆心角等于 61.2 度.
【分析】根据扇形统计图中的数据可以得到短信费所占的百分比,从而可以求得表示短信费的扇形的圆心角的度数.
【解答】解:360°×(1﹣4%﹣45%﹣34%)
=360°×17%
=61.2°,
故答案为:61.2.
11.(3分)下列方程:①x+2=0;②4x=8;③=3.其中解为x=2的是 ②③ (填序号).
【分析】把x=2代入各个方程,判断方程的左、右两边是否相等即可判断.
【解答】解:把x=2代入x+2=0,左边=4≠右边,所以不是方程的解,①错误;
把x=2代入方程4x=8,左边=8=右边,所以是方程的解,②正确;
把x=2代入方程=3,左边=3=右边,所以是方程的解,③正确.
故答案为:②③.
12.(3分)在有理数范围内定义一种新运算“⊕”,其运算规则为:a⊕b=﹣2a+3b,如1⊕5=﹣2×1+3×5=13,则方程2x⊕4=0的解为 x=3 .
【分析】根据a⊕b=﹣2a+3b,可以求得题目中方程的解.
【解答】解:∵a⊕b=﹣2a+3b,
∴2x⊕4=0
﹣2×2x+3×4=0
﹣4x+12=0
﹣4x=﹣12
x=3,
故答案为:x=3.
13.(3分)如今,中学生睡眠不足的问题正愈演愈烈,“缺觉”已是全国中学生们的老大难问题.教育部规定,初中生每天的睡眠时间应为9个小时.鹏鹏记录了他一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则鹏鹏这一周的睡眠够9个小时的有 2 天.
【分析】根据统计图中的数据可知,鹏鹏这一周的睡眠够9个小时的有几天,本题得以解决.
【解答】解:由图可知,
鹏鹏周一到周日的睡眠时间分别是:6小时,8小时,7小时,7小时,9小时,10小时,8小时,
则鹏鹏这一周的睡眠够9个小时的有2天,
故答案为:2.
14.(3分)如图,整个圆表示某班参加课外活动的总人数,跳绳的人数占30%,表示踢毽的扇形圆心角是60°,踢毽和打篮球的人数比是1:2,那么表示参加“其它”活动的人数占总人数的 20 %.
【分析】由“踢毽的扇形圆心角是60°,踢毽和打篮球的人数比是1:2”可得,踢毽的人数占总人数的比例以及打篮球的人数占的比例,由“各部分占总体的百分比之和为1”可得:参加“其它”活动的人数占总人数的比例.
【解答】解:由题意知,踢毽的人数占总人数的比例=60°÷360°=,
则打篮球的人数占的比例=×2=,
∴表示参加“其它”活动的人数占总人数的比例=1﹣﹣﹣30%=20%.
故答案为:20%.
三、解答题(共78分,解答要写出必要的文字说明、演算步骤)
15.(6分)如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
【分析】利用圆柱的体积计算公式进行计算,即可得到这个圆柱的体积.
【解答】解:由图可知,圆柱的半径r=12.56÷(2π)=2(dm),高h=4r=8dm,
则体积V=πr2h=3.14×22×8=100.48(dm3).
答:这个圆柱的体积是100.48dm3.
16.(6分)一辆货车从超市出发送货.先向南行驶30km到达A单位,继续向南行驶20km到达B单位.回到超市后,又给向北15km处的C单位送了3次货,然后回到超市休息.
(1)C单位离A单位有多远?
(2)该货车一共行驶了多少km?
【分析】(1)设超市为原点,向南为正,向北为负,然后列式进行求解;
(2)货车从超市到A到B,再回到超市,然后到C处三个来回,共六个单程距离.
【解答】解:(1)规定超市为原点,向南为正,向北为负,
依题意得C单位离A单位有:30+|﹣15|=45km,
∴C单位离A单位45km;
(2)该货车一共行驶了:
(30+20)×2+|﹣15|×6
=50×2+15×6
=100+90
=190km.
答:该货车一共行驶了190km.
17.(7分)一个花坛的形状如图所示,它的两端是半径相等的半圆,求:
(1)花坛的周长l;
(2)花坛的面积S;
(3)若a=8m,r=5m,求此时花坛的周长及面积(π取3.14).
【分析】(1)利用花坛的周长=圆的周长+长方形的两条边求解.
(2)利用花坛的面积=圆的面积+长方形的面积求解,
(3)把a=8m,r=5m,代入公式求解即可.
【解答】解:(1)花坛的周长l=2a+2πr,
(2)花坛的面积S=2ra+πr2,
(3)l=2a+2πr=16+10π=47.4(米),
S=2ra+πr2=2×5×8+3.14×25=158.5(平方米).
18.(8分)已知点A,B如图所示,请你按照下列要求画图(延长线都画成虚线):
(1)过点A,B画直线AB,并在直线AB上方任取两点C,D;
(2)画射线AC,线段CD;
(3)延长线段CD,与直线AB相交于点M;
(4)画线段DB,反向延长线段DB,与射线AC相交于点N.
【分析】(1)过点A,B画直线AB,并在直线AB上方任取两点C,D;
(2)画射线AC,线段CD;
(3)延长线段CD,与直线AB相交于点M;
(4)画线段DB,反向延长线段DB,与射线AC相交于点N.
【解答】解:答案不唯一,画出的图形如图所示:
19.(8分)如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=50°,∠DOE=35°,那么∠BOD是多少度?
(2)如果∠AOE=160°,∠COD=40°,那么∠AOB是多少度?
【分析】(1)可以根据角平分线的定义求得∠COD,∠BOC的度数,即可求∠BOD;
(2)根据角平分线的定义可求∠COE的度数,进而可求∠AOC的度数,再由角平分线即可求解∠AOB.
【解答】解:(1)∵OB是∠AOC的平分线,OD是∠COE的平分线
∴∠COD=∠DOE=35°,∠COB=∠BOA=50°
∴∠BOD=∠COD+∠COB=85°;
(2)∵OD是∠COE的平分线,
∴∠COE=2∠COD=2×40°=80°,
∴∠AOC=∠AOE﹣∠COE=160°﹣80°=80°,
又∵OB是∠AOC的平分线,
∴∠AOB=.
故答案为85°、40°.
20.(8分)根据以下对话,分别求小红所买的笔和笔记本的价格.
【分析】根据图中小红的回答,若设笔的价格为x元/支,则笔记本的价格为3x元/本.根据10支笔和5本笔记本花了30元钱,列出一元一次方程组10x+5×3x=30,解得x值,那么小红所买的笔和笔记本的价格即可确定.
【解答】解:设笔的价格为x元/支,则笔记本的价格为3x元/本
由题意,10x+5×3x=30
解之得x=1.2,3x=3.6
答:笔的价格为1.2元/支,则笔记本3.6元/本
21.(8分)某服装厂要生产某种型号的学生校服,已知3m长的某种布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,库内存这种布料600m,应如何分配布料做上衣和做裤子才能恰好配套?共能做多少套?
【分析】根据3m长的某种布料可做上衣2件或裤子3条,得出做上衣与裤子所用的布料关系,进而得出等式求出即可.
【解答】解:设做上衣的布料用xm,则做裤子的布料用(600﹣x)m,由题意得出:
×2=×3,
解得:x=360,
600﹣x=240(m).
答:做上衣的布料用360m,做裤子的布料用240m,才能恰好配套,共能做240套.
22.(8分)某人为了解他所在地区的旅游情况,收集了该地区2014年到2017年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题:
(1)该地区2014年到2017年四年的年旅游平均收入是多少亿元;
(2)从折线统计图中你能获得哪些信息?
【分析】(1)根据统计图中的数据可以计算出该地区2014年到2017年四年的年旅游平均收入是多少亿元;
(2)根据图形中的数据可以写出获得的信息,注意本题答案不唯一,只要符合实际即可.
【解答】解:(1)年旅游平均收入:(亿元),
答:该地区2014年到2017年四年的年旅游平均收入是55亿元;
(2)从折线统计图可得到:
①该地区从2014年到2017年,每年的年旅游收入逐年增加;
②2014年到2015年与2015年到2016年的年旅游收入增长量相等;
③2016年到2017年的年旅游收入增长速度最快.
23.(8分)为了迎接期末考试,某中学对全校七年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如图两幅不完整的统计图,请根据图中所给出的信息,解答下列问题:
(1)在这次调查中,被抽取的学生的总人数为多少?
(2)请将表示成绩类别为“中”的条形统计图补充完整.
(3)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角的度数是多少?[om]
(4)学校七年级共有1000人参加了这次数学考试,估计该校七年级共有多少名学生的数学成绩可以达到优秀.
【分析】(1)从两个统计图可得,“良”的有22人,占调查人数的44%,可求出调查人数;
(2)求出“中”的人数,即可补全条形统计图:
(3)求出“优”所占的百分比,可求出对应的圆心角的度数;
(4)样本估计总体,样本中“优秀”占20%,估计总体1000人的20%是“优秀”的人数.
【解答】解:(1)22÷44%=50(人)
答:被抽取的学生的总人数为50.
(2)50×20%=10(人),如图.
(3)因为成绩类别为“优”的扇形所占的百分比为10÷50=20%,
所以表示成绩类别为“优”的扇形所对应的圆心角的度数是360°×20%=72°,
(4)1000×20%=200(名).
答:估计该校七年级共有200名学生的数学成绩可以达到优秀.
24.(11分)如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为ts.
(1)当t=1时,PD=2AC,请求出AP的长;
(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
【分析】(1)(2)根据C、D的运动速度知BD=2PC,再由已知条件PD=2AC求得PB=2AP,由此求得AP的值;
(3)结合(1)、(2)进行解答;
(4)由题设画出图示,根据AQ﹣BQ=PQ求得AQ=PQ+BQ;然后求得AP=BQ,从而求得PQ与AB的关系.
【解答】解:(1)根据C、D的运动速度知:BD=2,PC=1,
则BD=2PC,
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∵AB=12cm,AB=AP+PB,
∴12=3AP,则AP=4cm;
(2)根据C、D的运动速度知:BD=4,PC=2,
则BD=2PC,
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∵AB=12cm,AB=AP+PB,
∴12=3AP,则AP=4cm;
(3)根据C、D的运动速度知:BD=2PC
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∴点P在线段AB上的处,即AP=4cm;
(4)如图:
∵AQ﹣BQ=PQ,
∴AQ=PQ+BQ;
又∵AQ=AP+PQ,
∴AP=BQ,
∴PQ=AB=4cm;
当点Q'在AB的延长线上时,
AQ′﹣AP=PQ′,
所以AQ′﹣BQ′=PQ=AB=12cm.
综上所述,PQ=4cm或12cm.
同课章节目录
