苏科版七年级数学下册11.3不等式的性质课件(18张PPT)
文档属性
| 名称 | 苏科版七年级数学下册11.3不等式的性质课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 337.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 09:18:04 | ||
图片预览





文档简介
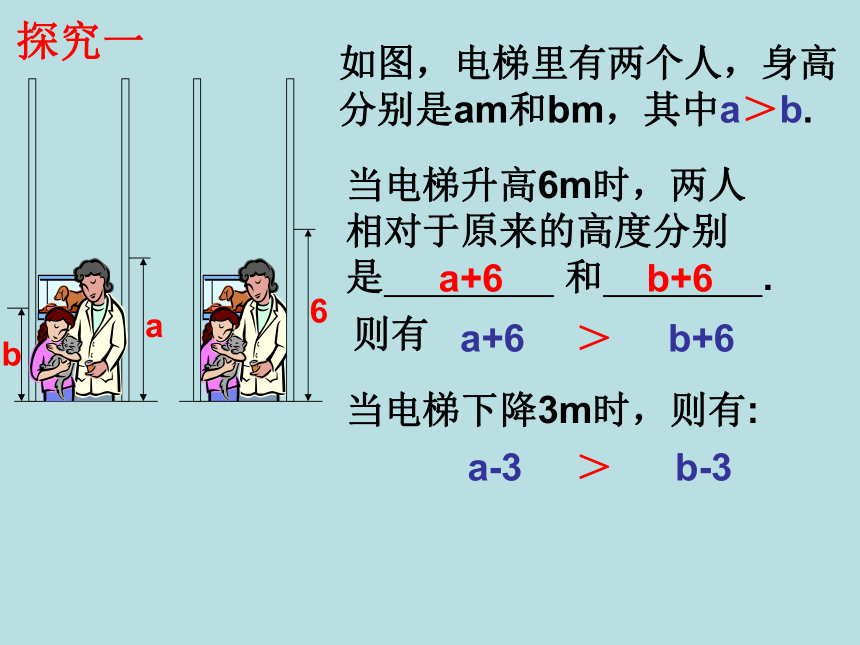
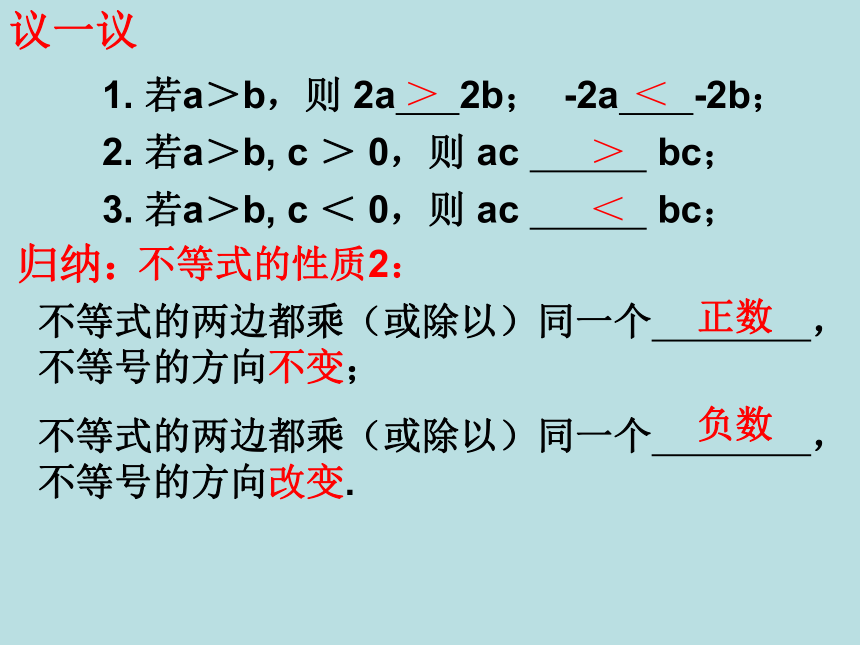
课件18张PPT。11.3 不等式的性质 小新栽了一棵小树,小树的高度是60cm,8周后,他发现小树长高了,且高度超过了100cm,问小树每周长高多少厘米?试一试解:设小树每周长高xcm,由题意可列不等式为60+8x>100ab如图,电梯里有两个人,身高分别是am和bm,其中a>b.当电梯升高6m时,两人相对于原来的高度分别是 和 .a+6b+6则有a+6b+6>当电梯下降3m时,则有:a-3b-3>探究一归纳一般地,如果a>b,那么a+c ___ b+c (或a-c ___b-c)>>不等式的性质1: 不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.结论:回忆:不等式的性质1与哪条等式的性质相似?等式的性质: 1. 等式两边都加上或减去同一个数(或同一个整式),等式仍成立.根据等式的性质2,你能说出不等式的其他性质吗? 2. 等式两边都乘或除以同一个数(除数不为0),等式仍成立.猜一猜:不等式的两边都乘(或除以)同一个数,不等号的方向都不变?请你将不等式6>3的两边分别乘同一个数,再比较积的大小。探究二你有什么发现?1. 若a>b,则 2a 2b; -2a -2b;2. 若a>b, c > 0,则 ac bc;3. 若a>b, c < 0,则 ac bc;><><不等式的性质2:不等式的两边都乘(或除以)同一个 ,不等号的方向不变;
不等式的两边都乘(或除以)同一个 ,不等号的方向改变.正数负数议一议归纳:1. 不等式的两边都乘以0,结果又怎样?2. 不等式的性质与等式的性质有什么相同点、
不同点?结果变为恒等式,即0 = 0.?
不等式与等式的性质比较
等式两边加上(减去)同一个数成同一个整式,方程仍成立
等式两边都乘以(或除以)同一个正数,方程仍成立
不等式的两边加上(或减去)同一个数或同一个整式,不等号的方向不变
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变
相同相同不相同练一练1.已知a<<<<>>(11) 若 b < c,则 a c .(12) 若c 下面各题的结论对吗?请说出你的观点和理由:
⑴ 如果 a+8>4,那么a>-4; ( )
⑵ 如果 2x>-4,那么x>-2; ( )
⑶ 因为-0.5m<-1,所以m>2; ( )
⑷ 如果3x⑸ 如果a>b,那么ac2>bc2; ( )
⑹ 如果ac2>bc2,那么a>b. ( )
看谁说的好!x>4x<-1.5x <1.5将下列不等式化成“x>a”或“x<a”的形式:
(1)x - 5>-1
(2)-2x>3
(3)2x- 1<2
(4)2x <例题 小新栽了一棵小树,小树的高度是60cm,8周后,他发现小树长高了,且高度超过了100cm,问小树每周长高多少厘米?你能利用不等式的性质化简吗?解:设小树每周长高xcm,由题意可列不等式为60+8x>100 不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.1.不等式的性质1:2.不等式的性质2: 不等式的两边都乘(或除以)同个正数,不等号的方向不变;不等式的两边都乘(或除以)同一个负数,不等号的方向改变.3.可根据不等式的性质,把不等式进行变形,化为x >a或x <a的形式.1. 请用不等式表示:“如果实数a是负数,那么它的相反数是正数”.2. 将不等式mx>m(m≠0)的两边都除以m,可得到哪些结论?如果a<0,那么- a >0.当m>0时, x>1; m < 0时, x < 1.3. 该不等式的变形错在哪里?
将不等式2x>4x 的两边都除以x,得2 >4.4. 把不等式-1> x变形为x <- 1,你觉得对吗?
已知不等式 (m-1)x > m-1 的解集为 x < 1 ,求m的范围。考考你挑战新高根据不等式的性质,我们可以得到比较两个数的大小的方法“作差法”:
(1)若 ,则A>B;
(2)若 ,则A=B;
(3)若 ,则A (1)
(2)和-2m+5;和-4a+1.看谁答的快!⑴ x- 3 >0 , x ,
⑵ x + 5 < 2, x ,
⑶ 3x ≥ -9, x ,
⑷ -3x ≤ 0, x ,
⑸ x > x, x ,
⑹ 6-2x>0, x ,> 3< -3≥ -3≥ 0> 0< 3
不等式的两边都乘(或除以)同一个 ,不等号的方向改变.正数负数议一议归纳:1. 不等式的两边都乘以0,结果又怎样?2. 不等式的性质与等式的性质有什么相同点、
不同点?结果变为恒等式,即0 = 0.?
不等式与等式的性质比较
等式两边加上(减去)同一个数成同一个整式,方程仍成立
等式两边都乘以(或除以)同一个正数,方程仍成立
不等式的两边加上(或减去)同一个数或同一个整式,不等号的方向不变
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变
相同相同不相同练一练1.已知a
⑴ 如果 a+8>4,那么a>-4; ( )
⑵ 如果 2x>-4,那么x>-2; ( )
⑶ 因为-0.5m<-1,所以m>2; ( )
⑷ 如果3x
⑹ 如果ac2>bc2,那么a>b. ( )
看谁说的好!x>4x<-1.5x <1.5将下列不等式化成“x>a”或“x<a”的形式:
(1)x - 5>-1
(2)-2x>3
(3)2x- 1<2
(4)2x <例题 小新栽了一棵小树,小树的高度是60cm,8周后,他发现小树长高了,且高度超过了100cm,问小树每周长高多少厘米?你能利用不等式的性质化简吗?解:设小树每周长高xcm,由题意可列不等式为60+8x>100 不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.1.不等式的性质1:2.不等式的性质2: 不等式的两边都乘(或除以)同个正数,不等号的方向不变;不等式的两边都乘(或除以)同一个负数,不等号的方向改变.3.可根据不等式的性质,把不等式进行变形,化为x >a或x <a的形式.1. 请用不等式表示:“如果实数a是负数,那么它的相反数是正数”.2. 将不等式mx>m(m≠0)的两边都除以m,可得到哪些结论?如果a<0,那么- a >0.当m>0时, x>1; m < 0时, x < 1.3. 该不等式的变形错在哪里?
将不等式2x>4x 的两边都除以x,得2 >4.4. 把不等式-1> x变形为x <- 1,你觉得对吗?
已知不等式 (m-1)x > m-1 的解集为 x < 1 ,求m的范围。考考你挑战新高根据不等式的性质,我们可以得到比较两个数的大小的方法“作差法”:
(1)若 ,则A>B;
(2)若 ,则A=B;
(3)若 ,则A
(2)和-2m+5;和-4a+1.看谁答的快!⑴ x- 3 >0 , x ,
⑵ x + 5 < 2, x ,
⑶ 3x ≥ -9, x ,
⑷ -3x ≤ 0, x ,
⑸ x > x, x ,
⑹ 6-2x>0, x ,> 3< -3≥ -3≥ 0> 0< 3
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
