2020春中考数学专题——几何动点运动轨迹及最值专题讲义(PDF版,无答案)
文档属性
| 名称 | 2020春中考数学专题——几何动点运动轨迹及最值专题讲义(PDF版,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 602.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 17:32:38 | ||
图片预览




文档简介
第 1 页 共 16 页
2020春中考数学几何动点运动轨迹及最值专题讲义
一、动点运动轨迹——直线型(动点轨迹为一条直线,利用“垂线段最短”)
Ⅰ.当一个点的坐标以某个字母的代数式表示,若可化为一次函数,则点的轨迹是直线;
1.在平面直角坐标系中,点 P的坐标为(0,2),点M的坐标为
3 9
( 1, )
4 4
m m? ? ? (其中 m为实数),当 PM
的长最小时,m的值为__________.
2.如图,在平面直角坐标系中,A(1,4),B(3,2),C(m,-4m+20),若 OC恰好平分四边形...OACB....的面
积,求点 C的坐标.
Ⅱ.当某一动点到某条直线的距离不变时,该动点的轨迹为直线;
3.如图,矩形 ABCD中,AB=6,AD=8,点 E 在边 AD 上,且 AE:ED=1:3.动点 P 从点 A 出发,沿
AB运动到点 B停止.过点 E作 EF⊥PE交射线 BC于点 F,设M是线段 EF的中点,则在点 P运动的整
个过程中,点 M运动路线的长为_________.
【变式 1】如图,矩形 ABCD中,AB=6,AD=8,点 E在边 AD上,且 AE:ED=1:3.动点 P从点 A出
发,沿 AB 运动到点 B 停止.过点 E 作 EF⊥PE 交边 BC 或 CD 于点 F,设 M 是线段 EF 的中
点,则在点 P运动的整个过程中,点M运动路线的长为___________.
A
B
D
C
E
F
P
M
A
B
D
C
E
F
P
M
y
x
B
A
O
第 2 页 共 16 页
【变式 2】如图,在矩形 ABCD中,点 P在 AD上,AB=2,AP=1,E是 AB上的一个动点,连接 PE,过
点 P作 PE的垂线,交 BC于点 F,连接 EF,设 EF的中点为 G,当点 E从点 B运动到点 A时,
点 G移动的路径的长是_________.
【变式 3】在矩形 ABCD中,AB=4,AD=6,P是 AD边的中点,点 E在 AB边上,EP的延长线交射线 CD
于 F点,过点 P作 PQ⊥EF,与射线 BC相交于点 Q.
(1)如图 1,当点 Q在点 C时,试求 AE的长;
(2)如图 2,点 G为 FQ的中点,连结 PG.
①当 AE=1 时,求 PG的长;
②当点 E从点 A运动到点 B时,试直接写出线段 PG扫过的面积. 变式 3 图 1
4.如图,C、D 是线段 AB 上两点,且 AC=BD=
1
6
AB=1,点 P 是线段 CD 上一个动点,在 AB 同侧分别
作等边△PAE 和等边△PBF,M为线段 EF 的中点。在点 P 从点 C移动到点 D 时,点 M 运动的路径长度
为__________.
A
B
D
C
P
(Q)
E
F
A
B
D
C
P
Q
E
F
G
变式 3 图 2
A BC D
E
F
P
M
第 3 页 共 16 页
【变式 1】已知 AB=10,点 C、D在线段 AB上且 AC=DB=2;P是线段 CD上的动点,分别以 AP、PB为
边在线段 AB的同侧作正方形 APEF和正方形 PBGH,点 O1 和 O2 是这两个正方形的中心,连接
O1O2,设 O1O2 的中点为 Q;当点 P从点 C运动到点 D时,则点 Q移动路径的长是_________.
【变式 2】等边三角形 ABC中,BC=6,D、E是边 BC上两点,且 BD=CE=1,点 P是线段 DE上的一个
动点,过点 P分别作 AC、AB的平行线交 AB、AC于点 M、N,连接MN、AP交于点 G,则点 P
由点 D移动到点 E的过程中,线段 BG扫过的区域面积为______.
【变式 3】如图,四边形 ABHK 是边长为 6 的正方形,点 C、D 在边 AB 上,且 AC=DB=1,点 P 是线段
CD上的动点,分别以 AP、PB为边在线段 AB的同侧作正方形 AMNP和正方形 BRQP,E、F分
别为 MN、QR 的中点,连接 EF,设 EF的中点为 G,则当点 P从点 C 运动到点 D 时,点 G 移
动的路径长为______.
5.如图,已知在四边形 ABCD中,AD∥BC,AB⊥BC,AD=1,BC=3,P为 AB边上的一动点,连接 PD
并延长到点 E,使得 PD∶PE=1∶3,以 PE,PC为边作平行四边形 PEFC,连接 PF,则 PF的最小值为
__________.
A
B C
D
E
F
P
B C
D E
M
N
P
G
A
A B
C D
E
F
GH
P
O
OQ 2
1
A B
C D
NM
RQ
P
HK
E
F
G
第 4 页 共 16 页
【延伸】在四边形 ABCD 中,AB∥CD,BC⊥CD,AB=3,CD=4,在 BC上取点 P(P与 B、C不重合),
连接 PA延长至 E,使 PE∶PA=x∶1,连接 PD并延长到 F,使 PF∶PD=y∶1(x,y>1),以 PE、
PF为边作平行四边形,另一个顶点为 G,求 PG长度的最小值(用 x,y表示).
【同型练】如图,已知矩形 OABC的顶点 A、C分别在直线 x=1 和 x=4 上,O是坐标原点,则对角线 OB
长的最小值为______.
Ⅲ.当某一动点与定线段一个端点连接后成的角度不变,则该动点轨迹是直线。
6 .如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为 AC中点,若点
D在直线 BC上运动,连接 OE,则在点 D运动过程中,线段 OE的最小值是为__________.
【变式】如图,边长为 2a 的等边△ABC 中,M 是高 CH 所在直线上的一个动点,连接 MB,将线段 BM 绕
点 B逆时针旋转 60°得到 BN,连接 HN.则在点M运动过程中,线段 HN长度的最小值是________.
y
x
B
C
O
A
A B
CD
P
E
F
G
A B
C
H
M
N
第 5 页 共 16 页
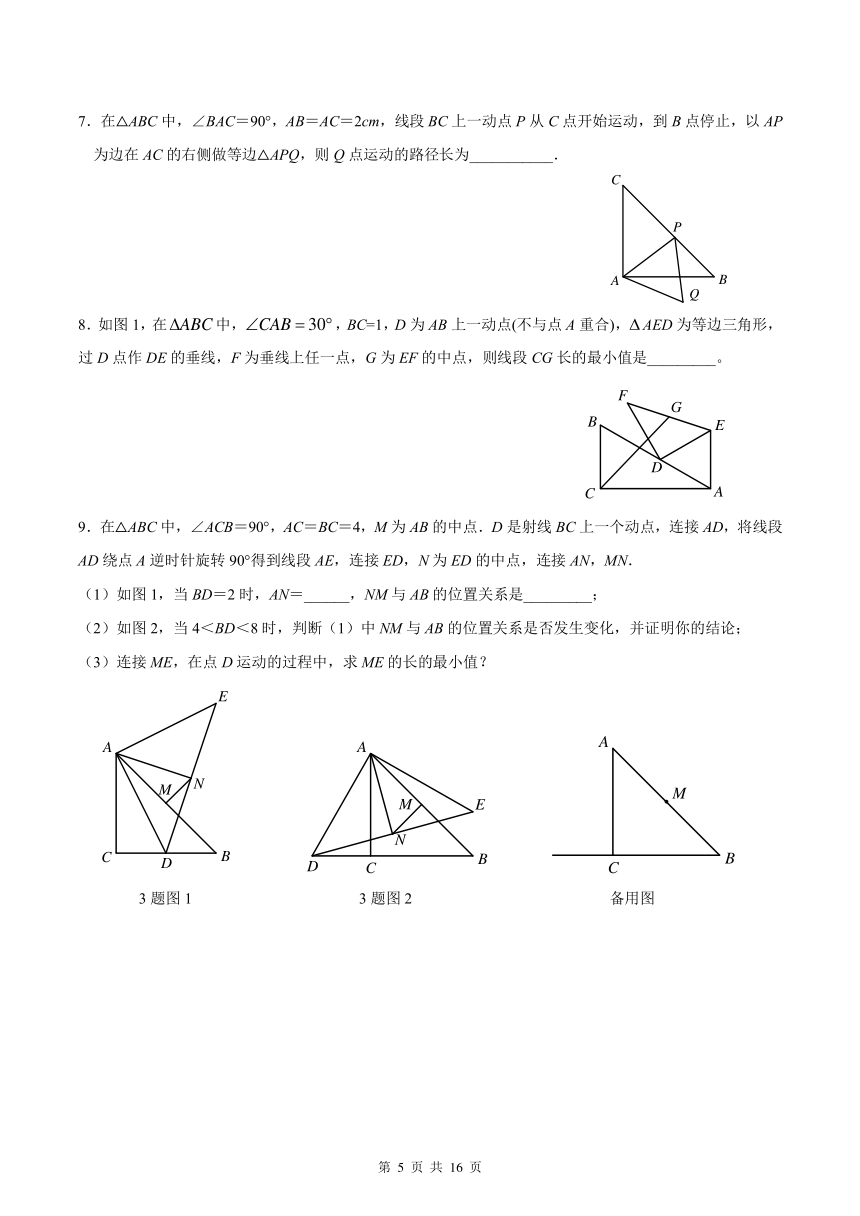
7.在△ABC中,∠BAC=90°,AB=AC=2cm,线段 BC上一动点 P从 C点开始运动,到 B点停止,以 AP
为边在 AC的右侧做等边△APQ,则 Q点运动的路径长为___________.
8.如图 1,在 ABC? 中, 30CAB? = ?,BC=1,D为 AB上一动点(不与点 A重合),? AED为等边三角形,
过 D点作 DE的垂线,F为垂线上任一点,G为 EF的中点,则线段 CG长的最小值是_________。
9.在△ABC中,∠ACB=90°,AC=BC=4,M为 AB的中点.D是射线 BC上一个动点,连接 AD,将线段
AD绕点 A逆时针旋转 90°得到线段 AE,连接 ED,N为 ED的中点,连接 AN,MN.
(1)如图 1,当 BD=2 时,AN=______,NM与 AB的位置关系是_________;
(2)如图 2,当 4<BD<8 时,判断(1)中 NM与 AB的位置关系是否发生变化,并证明你的结论;
(3)连接ME,在点 D运动的过程中,求ME的长的最小值?
3 题图 1 3 题图 2 备用图
C B
A
M
D
E
N
C
B
A
M
D
E
N
C
B
A
M
A B
C
P
Q
A
B
C
D
E
F
G
第 6 页 共 16 页
【秒杀训练】
10.点 A的坐标为(-1,0),点 B在直线 y x= 上运动,当线段 AB最短时,点 B的坐标为( )
A. (0,0) B.
1 1
( , )
2 2
? ? C.
2 2
( , )
2 2
? D.
1 1
( , )
2 2
? ?
11.如图,⊙O的半径为 2,点 O到直线 l的距离为 3,点 P是直线 l上的一个动点,PQ切⊙O于点 Q,则
PQ的最小值为( )
A. 13 B. 5
C.3 D.2
12.如图,等腰梯形 ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是 BC的中点。
(1)求证:△MDC是等边三角形;
(2)将△MDC绕点 M旋转,当MD(即MD?)与 AB交于一点 E,MC(即MC?)同时与 AD交于一点 F
时,点 E,F和点 A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在,请说明理由;如果存
在,请计算出△AEF周长的最小值。
O
Q
l
P
A
B C
D
M
D'
C'
F
E
第 7 页 共 16 页
二、动点运动轨迹——圆或圆弧型(动点轨迹为定圆,利用三点共线)
Ⅰ.当动点到定点的距离不变..........时.,动点的轨迹是圆或圆弧;
13.如图,在正方形 ABCD中,边长为 2,点 E 是 AB 的中点,点 F 是 BC边上任意一点,将△BEF 沿 EF
所在直线折叠得到△PEF,连接 AP、CP,则 CP的最小值________,AP的最小值是_________.
14.如图,正方形 ABCD的边长为 2,将长为 2 的线段 QF的两端放在正方形相邻的两边上同时滑动.如果
点 Q从点 A出发,沿图中所示方向按 A→B→C→D→A滑动到点 A为止,同时点 F从点 B出发,沿图中所
示方向按 B→C→D→A→B 滑动到点 B 为止,那么在这个过程中,线段 QF 的中点 M 所经过的路线围成的
图形的面积为_____________.
【变式 1】在矩形 ABCD中,已知 AB=2cm,BC=3cm,现有一根长为 2cm的木棒 EF紧贴着矩形的边(即
两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒 EF 的中点 P 在运动过程中所
围成的图形的面积_______cm2.
【变式 2】如图,在矩形 ABCD中,AB=2,AD=3,点 E、F分别为 AD、DC边上的点,且 EF=2,点 G
为 EF的中点,点 P为 BC上一动点,则 PA+PG的最小值为________.
A
B C
D
Q
F
M
A
B C
D
E
F
P
A B
CD
E
F
P
A
B C
DE
F
G
P
第 8 页 共 16 页
【变式 3】如图,一根木棒 AB 长为 2a,斜靠在与地面 OM 垂直的墙壁 ON 上,与地面的倾斜角∠ABO=
60°,若木棒沿直线 NO下滑,且 B端沿直线 OM向右滑行,则木棒中点 P也随之运动,已知 A
端下滑到 A′时,AA′=( 3 2? )a,则木棒中点 P随之运动到 P′所经过的路线长_______________.
15.如图,在△ABC中,AC=2,AB=3.当∠B最大时,BC的长为________.
16.如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是 AB边上的动点(不与点 B重合),将△BCP沿
CP所在的直线翻折,得到△B′CP,连接 B′A,则 B′A长度的最小值是________.
17.如图,在□ABCD中,∠BCD=30°,BC=4,CD=3 3,M 是 AD 边的中点,N是 AB 边上的一动点,
将△AMN沿 MN所在直线翻折得到△A′MN,连接 A′C,则 A′C长度的最小值是________.
18.如图,在等腰 Rt△ABC 中,AC=BC=2 2,点 P 在以斜边 AB 为直径的半圆上,M 为 PC 的中点.当
点 P沿半圆从点 A运动至点 B时,点 M运动的路径长是________.
A
B
N
O M
A'
B'
P P'
A B
C
A
BC
P
M
第 9 页 共 16 页
19.如图,矩形 ABCD 中,AD=2AB=4,长度为 2 的动线段 AE 绕点 A 旋转,连接 EC,取 EC 的中点 F,
连接 DF,则 DF的取值范围为________。
Ⅱ.当某条边与该边所对的角是定值时,该角的顶点的轨迹是圆弧.
见.直角→找.斜边(定长)→想.直径→定.外心→现.“圆”形;
见.定角→找.对边(定长)→想.周角→转.心角→现.“圆”形;
20.如图,以 G(0,1)为圆心,半径为 2 的圆与 x 轴交于 A、B 两点,与 y轴交于 C、D 两点,点 E 为⊙G
上一动点,CF⊥AE于 F,当点 E从点 B出发顺时针运动到点 D时,点 F所经过的路径长为__________.
s
21.如图,矩形 OABC 的边 OA、OC分别在 x轴、y轴上,点 B 的坐标为(7,3),点 E在边 AB上,且 AE
=1,若点 P为 y轴上一动点,连接 EP,过点 O作直线 EP的垂线段,垂足为点 H,在点 P从 F(0,
25
4
)运
动到原点 O的过程中,点 H的运动路径长为______.
22.在正方形 ABCD中,AD=2,点 E从 D出发向终点 C运动,点 F从 C出发向终点 B运动,且始终保持
DE=CF,连接 AE和 DF交于点 P,则 P点运动的路径长是________.
y
x
F
H
E
A
C B
O
P
A
B C
D
E
F
A
B C
D
E
F
P
y
x
F
C
BA
D
G
E
第 10 页 共 16 页
23.等腰 Rt△ABC 中,∠C=90°,AC=BC=4,D 为线段 AC 上一动点,连接 BD,过点 C 作 CH⊥BD 于
H,连接 AH,则 AH的最小值为______.
24.如图,Rt△ABC 中,AB⊥BC,AB=6,BC=4,P 是△ABC 内部的一个动点,且满足∠PAB=∠PBC,
则线段 CP长的最小值为________.
25.如图,在边长为 2 3的等边△ABC中,动点 D从 C向终点 B运动,同时点 E以相同的速度从 A出发向
终点 C运动,连接 BE、AD相交于点 P,则点 P的路径长为________.
26.如图,⊙O的半径为 1,弦 AB=1,点 P为优弧 AB上一动点,AC⊥AP交直线 PB于点 C,则△ABC的
最大面积是____________.
27.如图,已抛物线 y=ax2+bx+c(a≠0)与 x轴交于 A(1,0)、B(4,0)两点,与 y轴交于 C(0,2),连结 AC、
BC.
(1)求抛物线解析式;
(2)BC的垂直平分线交抛物线于 D、E两点,求直线 DE的解析式;
(3)若点 P在抛物线的对称轴上,且∠CPB=∠CAB,求出所有满足条件的 P点坐标.
y
x
C
BO A
A
BC
D
H
A
CB
P
A
CB D
E
P
O
A
B
P
C
第 11 页 共 16 页
28.如图,在正方形 ABCD中,AB=2,动点 E从点 A出发向点 D运动,同时动点 F从点 D出发向点 C运
动,点 E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段 AF、BE相交于点 P,则
线段 DP的最小值为__________。
【变式】直线 y=x+4 分别与 x轴、y轴相交与点 M、N,边长为 2 的正方形 OABC一个顶点 O在坐标系的
原点,直线 AN与MC相交于 P,若正方形绕着点 O旋转一周,则点 P到点(0,2)长度的最小值是
__________.
29.如图,边长为 3 的正方形 ABCD,两顶点 A、B分别在平面直角坐标系的 x轴、y 轴的正半轴上滑动,
点 C点 D在第一象限,点 E为正方形 ABCD的对称中心,连结 OE,则 OE的长的最大值是__________.
【变式】如图,已知平面直角坐标系中,直线 y=kx(k≠0)经过点 C(a,3a)(a>0).线段 BC 的两个端点分
别在 x轴与直线 y=kx上(B、C均与原点 O不重合)滑动,且 BC=2,分别作 BP⊥x轴,CP⊥直
线 y=kx,交点为 P,经探究在整个滑动过程中,P、O两点间的距离为定值.
A
B C
DE
F
P
y
x
E
D
C
A
B
O
y
x
P
C
O B
y
x
P
A
C B
N
M
O
第 12 页 共 16 页
30.如图 1,开口向下的抛物线 2( 2)y a x k= ? + 交 x轴于点 A,B两点,交 y轴正半轴于点 C,顶点为 P,
过顶点 P作 x轴,y轴的垂线,垂足分别为M,N,连结 CP,CM,∠CPM=45°,tan∠CMP=0.8.
(1)求该抛物线的函数解析式;
(2)如图 2,若点 D为射线 PC上的动点,BD交△PMD的外接圆于点 Q,求 PQ的最小值.
图 1 图 2
【强化训练】
31.如图,△ABC 中,AC=3,BC=4 2 ,∠ACB=45°,D 为△ABC 内一动点,⊙O 为△ACD 的外接圆,
交 BC于 E点,直线 BD交⊙O于 P点,弧 AE=CP,则 AD的最小值为_______
【练】如图,在△ABC中,AC=3,BC=4 2 ,∠ACB=45°,AM∥BC,点 P在射线 AM上运动,连 BP交
△APC的外接圆于 D,则 AD的最小值为_______
A
B C
D
O
P
M
y
x
B
C
N
M
P
A
O
y
x
Q
B
C
M
P
A
O
D
A
B C
D
O
E
P
第 13 页 共 16 页
32.如图,AC=3,BC=5,且∠BAC=90°,D为 AC上一动点,以 AD为直径作圆,连接 BD交圆于 E点,
连 CE,则 CE的最小值为_______
33.如图,A(1,0)、B(3,0),以 AB为直径作⊙M,射线 OF 交⊙M 于 E、F 两点,C为弧 AB 的中点,D
为 EF的中点.当射线绕 O点旋转时,CD的最小值为__________
34.如图,AB是⊙O的直径,AB=2,∠ABC=60°,P是 BC上一动点,D是 AP的中点,连接 CD,则 CD
的最小值为__________
35.如图,在动点 C与定长线段 AB组成的△ABC中,AB=6,AD⊥BC于点 D,BE⊥AC于点 E,连接 DE.当
点 C在运动过程中,始终有
2
2
DE
AB
= ,则点 C到 AB的距离的最大值是_________
36.如图,已知以 BC 为直径的⊙O,A 为弧 BC 中点,P 为弧 AC 上任意一点,AD⊥AP 交 BP 于 D,连
CD.若 BC=8,则 CD的最小值为___________。
A
B C
O
P
D
A B
C
D
E
A B
C
O
P
D
A
B C
D
O
E
y
x
C
D
F
M BO A
E
第 14 页 共 16 页
三、动点轨迹为其他曲线,构造三角形
37.如图,∠MON=90°,矩形 ABCD的顶点 A、B分别在边 OM,ON上,当 B在边 ON上运动时,A随之
在边 OM上运动,矩形 ABCD的形状保持不变,其中 AB=2,BC=1,求运动过程中,点 D到点 O的最大距
离.
38.如图,在 Rt△ABC中,∠ACB=90°,BC=6,tan∠BAC=
1
2
,点 D在边 AC的三等分点处,将线段 AD绕
点 A旋转,连接 BD,F为 BD中点,求线段 CF长度的最大值.
39.如图,在△ABC中,∠C=90°,AC=2,BC=1,点 A、C分别在 x轴、y轴上,当点 A在 x轴运动时,
点 C随之在 y轴上运动,在运动过程中,点 B到原点 O的最大距离为___________。
40.如图,∠MON=90°,线段 AB 两端点分别在边 OM,ON上,当 A 在边 OM 上运动时,B 随之在边 ON
上运动,AB=2 保持不变,以 AB 为边向外作等边△ABC,在运动过程中,四边形 AOBC 的面积的最大值是
___________.
A
B
C
D
O N
M
A
BC
D
F
A
B
C
O
M
N
y
xO
C
A
B
第 15 页 共 16 页
41.如图,平面直角坐标系中,将含 30°的三角尺的直角顶点 C落在第二象限.其斜边两端点 A、B分别落
在 x轴、y轴上,且 AB=12cm.
(1)若 OB=6cm.
①求点 C的坐标;
②若点 A向右滑动的距离与点 B向上滑动的距离相等,求滑动的距离;
(2)点 C与点 O的距离的最大值=___________cm.
四、双动点型
I.利用等量代换实现转化
42.△ABC是以 AB为斜边的直角三角形,AC=4,BC=3,P是 AB上一动点,且 PE⊥AC于 E,PF⊥BF于
F,求 EF的最小值.
II.利用和差关系实现转化
43.如图,在△ABC中,AB=10,AC=8,BC=6,经过点 C且与边 AB相切的动圆与 CA,CB分别相交于点
P,Q,则线段 PQ长度的最小值是___________.
III.利用勾股定理实现转化
44.如图,在 Rt△AOB中,OA=OB=3 2 ,圆 O的半径为 1,点 P是 AB边上的动点,过点 P作圆 O的一
条切线 PQ(点 Q为切点),则切线 PQ的最小值为______.
A
BO
Q
P
B
AC P
Q
A
B
C
E
F
P
y
x
C
B
A O
第 16 页 共 16 页
IV.利用三角形边角关系实现转化
45.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段 BC上的一个动点,以 AD为直径画 O分
别交于 AB、AC于 E、F,连接 EF,则线段 EF长度的最小值为__________.
A
B CD
O
E
F
2020春中考数学几何动点运动轨迹及最值专题讲义
一、动点运动轨迹——直线型(动点轨迹为一条直线,利用“垂线段最短”)
Ⅰ.当一个点的坐标以某个字母的代数式表示,若可化为一次函数,则点的轨迹是直线;
1.在平面直角坐标系中,点 P的坐标为(0,2),点M的坐标为
3 9
( 1, )
4 4
m m? ? ? (其中 m为实数),当 PM
的长最小时,m的值为__________.
2.如图,在平面直角坐标系中,A(1,4),B(3,2),C(m,-4m+20),若 OC恰好平分四边形...OACB....的面
积,求点 C的坐标.
Ⅱ.当某一动点到某条直线的距离不变时,该动点的轨迹为直线;
3.如图,矩形 ABCD中,AB=6,AD=8,点 E 在边 AD 上,且 AE:ED=1:3.动点 P 从点 A 出发,沿
AB运动到点 B停止.过点 E作 EF⊥PE交射线 BC于点 F,设M是线段 EF的中点,则在点 P运动的整
个过程中,点 M运动路线的长为_________.
【变式 1】如图,矩形 ABCD中,AB=6,AD=8,点 E在边 AD上,且 AE:ED=1:3.动点 P从点 A出
发,沿 AB 运动到点 B 停止.过点 E 作 EF⊥PE 交边 BC 或 CD 于点 F,设 M 是线段 EF 的中
点,则在点 P运动的整个过程中,点M运动路线的长为___________.
A
B
D
C
E
F
P
M
A
B
D
C
E
F
P
M
y
x
B
A
O
第 2 页 共 16 页
【变式 2】如图,在矩形 ABCD中,点 P在 AD上,AB=2,AP=1,E是 AB上的一个动点,连接 PE,过
点 P作 PE的垂线,交 BC于点 F,连接 EF,设 EF的中点为 G,当点 E从点 B运动到点 A时,
点 G移动的路径的长是_________.
【变式 3】在矩形 ABCD中,AB=4,AD=6,P是 AD边的中点,点 E在 AB边上,EP的延长线交射线 CD
于 F点,过点 P作 PQ⊥EF,与射线 BC相交于点 Q.
(1)如图 1,当点 Q在点 C时,试求 AE的长;
(2)如图 2,点 G为 FQ的中点,连结 PG.
①当 AE=1 时,求 PG的长;
②当点 E从点 A运动到点 B时,试直接写出线段 PG扫过的面积. 变式 3 图 1
4.如图,C、D 是线段 AB 上两点,且 AC=BD=
1
6
AB=1,点 P 是线段 CD 上一个动点,在 AB 同侧分别
作等边△PAE 和等边△PBF,M为线段 EF 的中点。在点 P 从点 C移动到点 D 时,点 M 运动的路径长度
为__________.
A
B
D
C
P
(Q)
E
F
A
B
D
C
P
Q
E
F
G
变式 3 图 2
A BC D
E
F
P
M
第 3 页 共 16 页
【变式 1】已知 AB=10,点 C、D在线段 AB上且 AC=DB=2;P是线段 CD上的动点,分别以 AP、PB为
边在线段 AB的同侧作正方形 APEF和正方形 PBGH,点 O1 和 O2 是这两个正方形的中心,连接
O1O2,设 O1O2 的中点为 Q;当点 P从点 C运动到点 D时,则点 Q移动路径的长是_________.
【变式 2】等边三角形 ABC中,BC=6,D、E是边 BC上两点,且 BD=CE=1,点 P是线段 DE上的一个
动点,过点 P分别作 AC、AB的平行线交 AB、AC于点 M、N,连接MN、AP交于点 G,则点 P
由点 D移动到点 E的过程中,线段 BG扫过的区域面积为______.
【变式 3】如图,四边形 ABHK 是边长为 6 的正方形,点 C、D 在边 AB 上,且 AC=DB=1,点 P 是线段
CD上的动点,分别以 AP、PB为边在线段 AB的同侧作正方形 AMNP和正方形 BRQP,E、F分
别为 MN、QR 的中点,连接 EF,设 EF的中点为 G,则当点 P从点 C 运动到点 D 时,点 G 移
动的路径长为______.
5.如图,已知在四边形 ABCD中,AD∥BC,AB⊥BC,AD=1,BC=3,P为 AB边上的一动点,连接 PD
并延长到点 E,使得 PD∶PE=1∶3,以 PE,PC为边作平行四边形 PEFC,连接 PF,则 PF的最小值为
__________.
A
B C
D
E
F
P
B C
D E
M
N
P
G
A
A B
C D
E
F
GH
P
O
OQ 2
1
A B
C D
NM
RQ
P
HK
E
F
G
第 4 页 共 16 页
【延伸】在四边形 ABCD 中,AB∥CD,BC⊥CD,AB=3,CD=4,在 BC上取点 P(P与 B、C不重合),
连接 PA延长至 E,使 PE∶PA=x∶1,连接 PD并延长到 F,使 PF∶PD=y∶1(x,y>1),以 PE、
PF为边作平行四边形,另一个顶点为 G,求 PG长度的最小值(用 x,y表示).
【同型练】如图,已知矩形 OABC的顶点 A、C分别在直线 x=1 和 x=4 上,O是坐标原点,则对角线 OB
长的最小值为______.
Ⅲ.当某一动点与定线段一个端点连接后成的角度不变,则该动点轨迹是直线。
6 .如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为 AC中点,若点
D在直线 BC上运动,连接 OE,则在点 D运动过程中,线段 OE的最小值是为__________.
【变式】如图,边长为 2a 的等边△ABC 中,M 是高 CH 所在直线上的一个动点,连接 MB,将线段 BM 绕
点 B逆时针旋转 60°得到 BN,连接 HN.则在点M运动过程中,线段 HN长度的最小值是________.
y
x
B
C
O
A
A B
CD
P
E
F
G
A B
C
H
M
N
第 5 页 共 16 页
7.在△ABC中,∠BAC=90°,AB=AC=2cm,线段 BC上一动点 P从 C点开始运动,到 B点停止,以 AP
为边在 AC的右侧做等边△APQ,则 Q点运动的路径长为___________.
8.如图 1,在 ABC? 中, 30CAB? = ?,BC=1,D为 AB上一动点(不与点 A重合),? AED为等边三角形,
过 D点作 DE的垂线,F为垂线上任一点,G为 EF的中点,则线段 CG长的最小值是_________。
9.在△ABC中,∠ACB=90°,AC=BC=4,M为 AB的中点.D是射线 BC上一个动点,连接 AD,将线段
AD绕点 A逆时针旋转 90°得到线段 AE,连接 ED,N为 ED的中点,连接 AN,MN.
(1)如图 1,当 BD=2 时,AN=______,NM与 AB的位置关系是_________;
(2)如图 2,当 4<BD<8 时,判断(1)中 NM与 AB的位置关系是否发生变化,并证明你的结论;
(3)连接ME,在点 D运动的过程中,求ME的长的最小值?
3 题图 1 3 题图 2 备用图
C B
A
M
D
E
N
C
B
A
M
D
E
N
C
B
A
M
A B
C
P
Q
A
B
C
D
E
F
G
第 6 页 共 16 页
【秒杀训练】
10.点 A的坐标为(-1,0),点 B在直线 y x= 上运动,当线段 AB最短时,点 B的坐标为( )
A. (0,0) B.
1 1
( , )
2 2
? ? C.
2 2
( , )
2 2
? D.
1 1
( , )
2 2
? ?
11.如图,⊙O的半径为 2,点 O到直线 l的距离为 3,点 P是直线 l上的一个动点,PQ切⊙O于点 Q,则
PQ的最小值为( )
A. 13 B. 5
C.3 D.2
12.如图,等腰梯形 ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是 BC的中点。
(1)求证:△MDC是等边三角形;
(2)将△MDC绕点 M旋转,当MD(即MD?)与 AB交于一点 E,MC(即MC?)同时与 AD交于一点 F
时,点 E,F和点 A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在,请说明理由;如果存
在,请计算出△AEF周长的最小值。
O
Q
l
P
A
B C
D
M
D'
C'
F
E
第 7 页 共 16 页
二、动点运动轨迹——圆或圆弧型(动点轨迹为定圆,利用三点共线)
Ⅰ.当动点到定点的距离不变..........时.,动点的轨迹是圆或圆弧;
13.如图,在正方形 ABCD中,边长为 2,点 E 是 AB 的中点,点 F 是 BC边上任意一点,将△BEF 沿 EF
所在直线折叠得到△PEF,连接 AP、CP,则 CP的最小值________,AP的最小值是_________.
14.如图,正方形 ABCD的边长为 2,将长为 2 的线段 QF的两端放在正方形相邻的两边上同时滑动.如果
点 Q从点 A出发,沿图中所示方向按 A→B→C→D→A滑动到点 A为止,同时点 F从点 B出发,沿图中所
示方向按 B→C→D→A→B 滑动到点 B 为止,那么在这个过程中,线段 QF 的中点 M 所经过的路线围成的
图形的面积为_____________.
【变式 1】在矩形 ABCD中,已知 AB=2cm,BC=3cm,现有一根长为 2cm的木棒 EF紧贴着矩形的边(即
两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒 EF 的中点 P 在运动过程中所
围成的图形的面积_______cm2.
【变式 2】如图,在矩形 ABCD中,AB=2,AD=3,点 E、F分别为 AD、DC边上的点,且 EF=2,点 G
为 EF的中点,点 P为 BC上一动点,则 PA+PG的最小值为________.
A
B C
D
Q
F
M
A
B C
D
E
F
P
A B
CD
E
F
P
A
B C
DE
F
G
P
第 8 页 共 16 页
【变式 3】如图,一根木棒 AB 长为 2a,斜靠在与地面 OM 垂直的墙壁 ON 上,与地面的倾斜角∠ABO=
60°,若木棒沿直线 NO下滑,且 B端沿直线 OM向右滑行,则木棒中点 P也随之运动,已知 A
端下滑到 A′时,AA′=( 3 2? )a,则木棒中点 P随之运动到 P′所经过的路线长_______________.
15.如图,在△ABC中,AC=2,AB=3.当∠B最大时,BC的长为________.
16.如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是 AB边上的动点(不与点 B重合),将△BCP沿
CP所在的直线翻折,得到△B′CP,连接 B′A,则 B′A长度的最小值是________.
17.如图,在□ABCD中,∠BCD=30°,BC=4,CD=3 3,M 是 AD 边的中点,N是 AB 边上的一动点,
将△AMN沿 MN所在直线翻折得到△A′MN,连接 A′C,则 A′C长度的最小值是________.
18.如图,在等腰 Rt△ABC 中,AC=BC=2 2,点 P 在以斜边 AB 为直径的半圆上,M 为 PC 的中点.当
点 P沿半圆从点 A运动至点 B时,点 M运动的路径长是________.
A
B
N
O M
A'
B'
P P'
A B
C
A
BC
P
M
第 9 页 共 16 页
19.如图,矩形 ABCD 中,AD=2AB=4,长度为 2 的动线段 AE 绕点 A 旋转,连接 EC,取 EC 的中点 F,
连接 DF,则 DF的取值范围为________。
Ⅱ.当某条边与该边所对的角是定值时,该角的顶点的轨迹是圆弧.
见.直角→找.斜边(定长)→想.直径→定.外心→现.“圆”形;
见.定角→找.对边(定长)→想.周角→转.心角→现.“圆”形;
20.如图,以 G(0,1)为圆心,半径为 2 的圆与 x 轴交于 A、B 两点,与 y轴交于 C、D 两点,点 E 为⊙G
上一动点,CF⊥AE于 F,当点 E从点 B出发顺时针运动到点 D时,点 F所经过的路径长为__________.
s
21.如图,矩形 OABC 的边 OA、OC分别在 x轴、y轴上,点 B 的坐标为(7,3),点 E在边 AB上,且 AE
=1,若点 P为 y轴上一动点,连接 EP,过点 O作直线 EP的垂线段,垂足为点 H,在点 P从 F(0,
25
4
)运
动到原点 O的过程中,点 H的运动路径长为______.
22.在正方形 ABCD中,AD=2,点 E从 D出发向终点 C运动,点 F从 C出发向终点 B运动,且始终保持
DE=CF,连接 AE和 DF交于点 P,则 P点运动的路径长是________.
y
x
F
H
E
A
C B
O
P
A
B C
D
E
F
A
B C
D
E
F
P
y
x
F
C
BA
D
G
E
第 10 页 共 16 页
23.等腰 Rt△ABC 中,∠C=90°,AC=BC=4,D 为线段 AC 上一动点,连接 BD,过点 C 作 CH⊥BD 于
H,连接 AH,则 AH的最小值为______.
24.如图,Rt△ABC 中,AB⊥BC,AB=6,BC=4,P 是△ABC 内部的一个动点,且满足∠PAB=∠PBC,
则线段 CP长的最小值为________.
25.如图,在边长为 2 3的等边△ABC中,动点 D从 C向终点 B运动,同时点 E以相同的速度从 A出发向
终点 C运动,连接 BE、AD相交于点 P,则点 P的路径长为________.
26.如图,⊙O的半径为 1,弦 AB=1,点 P为优弧 AB上一动点,AC⊥AP交直线 PB于点 C,则△ABC的
最大面积是____________.
27.如图,已抛物线 y=ax2+bx+c(a≠0)与 x轴交于 A(1,0)、B(4,0)两点,与 y轴交于 C(0,2),连结 AC、
BC.
(1)求抛物线解析式;
(2)BC的垂直平分线交抛物线于 D、E两点,求直线 DE的解析式;
(3)若点 P在抛物线的对称轴上,且∠CPB=∠CAB,求出所有满足条件的 P点坐标.
y
x
C
BO A
A
BC
D
H
A
CB
P
A
CB D
E
P
O
A
B
P
C
第 11 页 共 16 页
28.如图,在正方形 ABCD中,AB=2,动点 E从点 A出发向点 D运动,同时动点 F从点 D出发向点 C运
动,点 E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段 AF、BE相交于点 P,则
线段 DP的最小值为__________。
【变式】直线 y=x+4 分别与 x轴、y轴相交与点 M、N,边长为 2 的正方形 OABC一个顶点 O在坐标系的
原点,直线 AN与MC相交于 P,若正方形绕着点 O旋转一周,则点 P到点(0,2)长度的最小值是
__________.
29.如图,边长为 3 的正方形 ABCD,两顶点 A、B分别在平面直角坐标系的 x轴、y 轴的正半轴上滑动,
点 C点 D在第一象限,点 E为正方形 ABCD的对称中心,连结 OE,则 OE的长的最大值是__________.
【变式】如图,已知平面直角坐标系中,直线 y=kx(k≠0)经过点 C(a,3a)(a>0).线段 BC 的两个端点分
别在 x轴与直线 y=kx上(B、C均与原点 O不重合)滑动,且 BC=2,分别作 BP⊥x轴,CP⊥直
线 y=kx,交点为 P,经探究在整个滑动过程中,P、O两点间的距离为定值.
A
B C
DE
F
P
y
x
E
D
C
A
B
O
y
x
P
C
O B
y
x
P
A
C B
N
M
O
第 12 页 共 16 页
30.如图 1,开口向下的抛物线 2( 2)y a x k= ? + 交 x轴于点 A,B两点,交 y轴正半轴于点 C,顶点为 P,
过顶点 P作 x轴,y轴的垂线,垂足分别为M,N,连结 CP,CM,∠CPM=45°,tan∠CMP=0.8.
(1)求该抛物线的函数解析式;
(2)如图 2,若点 D为射线 PC上的动点,BD交△PMD的外接圆于点 Q,求 PQ的最小值.
图 1 图 2
【强化训练】
31.如图,△ABC 中,AC=3,BC=4 2 ,∠ACB=45°,D 为△ABC 内一动点,⊙O 为△ACD 的外接圆,
交 BC于 E点,直线 BD交⊙O于 P点,弧 AE=CP,则 AD的最小值为_______
【练】如图,在△ABC中,AC=3,BC=4 2 ,∠ACB=45°,AM∥BC,点 P在射线 AM上运动,连 BP交
△APC的外接圆于 D,则 AD的最小值为_______
A
B C
D
O
P
M
y
x
B
C
N
M
P
A
O
y
x
Q
B
C
M
P
A
O
D
A
B C
D
O
E
P
第 13 页 共 16 页
32.如图,AC=3,BC=5,且∠BAC=90°,D为 AC上一动点,以 AD为直径作圆,连接 BD交圆于 E点,
连 CE,则 CE的最小值为_______
33.如图,A(1,0)、B(3,0),以 AB为直径作⊙M,射线 OF 交⊙M 于 E、F 两点,C为弧 AB 的中点,D
为 EF的中点.当射线绕 O点旋转时,CD的最小值为__________
34.如图,AB是⊙O的直径,AB=2,∠ABC=60°,P是 BC上一动点,D是 AP的中点,连接 CD,则 CD
的最小值为__________
35.如图,在动点 C与定长线段 AB组成的△ABC中,AB=6,AD⊥BC于点 D,BE⊥AC于点 E,连接 DE.当
点 C在运动过程中,始终有
2
2
DE
AB
= ,则点 C到 AB的距离的最大值是_________
36.如图,已知以 BC 为直径的⊙O,A 为弧 BC 中点,P 为弧 AC 上任意一点,AD⊥AP 交 BP 于 D,连
CD.若 BC=8,则 CD的最小值为___________。
A
B C
O
P
D
A B
C
D
E
A B
C
O
P
D
A
B C
D
O
E
y
x
C
D
F
M BO A
E
第 14 页 共 16 页
三、动点轨迹为其他曲线,构造三角形
37.如图,∠MON=90°,矩形 ABCD的顶点 A、B分别在边 OM,ON上,当 B在边 ON上运动时,A随之
在边 OM上运动,矩形 ABCD的形状保持不变,其中 AB=2,BC=1,求运动过程中,点 D到点 O的最大距
离.
38.如图,在 Rt△ABC中,∠ACB=90°,BC=6,tan∠BAC=
1
2
,点 D在边 AC的三等分点处,将线段 AD绕
点 A旋转,连接 BD,F为 BD中点,求线段 CF长度的最大值.
39.如图,在△ABC中,∠C=90°,AC=2,BC=1,点 A、C分别在 x轴、y轴上,当点 A在 x轴运动时,
点 C随之在 y轴上运动,在运动过程中,点 B到原点 O的最大距离为___________。
40.如图,∠MON=90°,线段 AB 两端点分别在边 OM,ON上,当 A 在边 OM 上运动时,B 随之在边 ON
上运动,AB=2 保持不变,以 AB 为边向外作等边△ABC,在运动过程中,四边形 AOBC 的面积的最大值是
___________.
A
B
C
D
O N
M
A
BC
D
F
A
B
C
O
M
N
y
xO
C
A
B
第 15 页 共 16 页
41.如图,平面直角坐标系中,将含 30°的三角尺的直角顶点 C落在第二象限.其斜边两端点 A、B分别落
在 x轴、y轴上,且 AB=12cm.
(1)若 OB=6cm.
①求点 C的坐标;
②若点 A向右滑动的距离与点 B向上滑动的距离相等,求滑动的距离;
(2)点 C与点 O的距离的最大值=___________cm.
四、双动点型
I.利用等量代换实现转化
42.△ABC是以 AB为斜边的直角三角形,AC=4,BC=3,P是 AB上一动点,且 PE⊥AC于 E,PF⊥BF于
F,求 EF的最小值.
II.利用和差关系实现转化
43.如图,在△ABC中,AB=10,AC=8,BC=6,经过点 C且与边 AB相切的动圆与 CA,CB分别相交于点
P,Q,则线段 PQ长度的最小值是___________.
III.利用勾股定理实现转化
44.如图,在 Rt△AOB中,OA=OB=3 2 ,圆 O的半径为 1,点 P是 AB边上的动点,过点 P作圆 O的一
条切线 PQ(点 Q为切点),则切线 PQ的最小值为______.
A
BO
Q
P
B
AC P
Q
A
B
C
E
F
P
y
x
C
B
A O
第 16 页 共 16 页
IV.利用三角形边角关系实现转化
45.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段 BC上的一个动点,以 AD为直径画 O分
别交于 AB、AC于 E、F,连接 EF,则线段 EF长度的最小值为__________.
A
B CD
O
E
F
同课章节目录
