高中数学人教新课标A版选修3-4第二讲代数学中的对称与抽象群的概念2.1 n元对称群Sn(共31张PPT)
文档属性
| 名称 | 高中数学人教新课标A版选修3-4第二讲代数学中的对称与抽象群的概念2.1 n元对称群Sn(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 704.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 22:26:34 | ||
图片预览








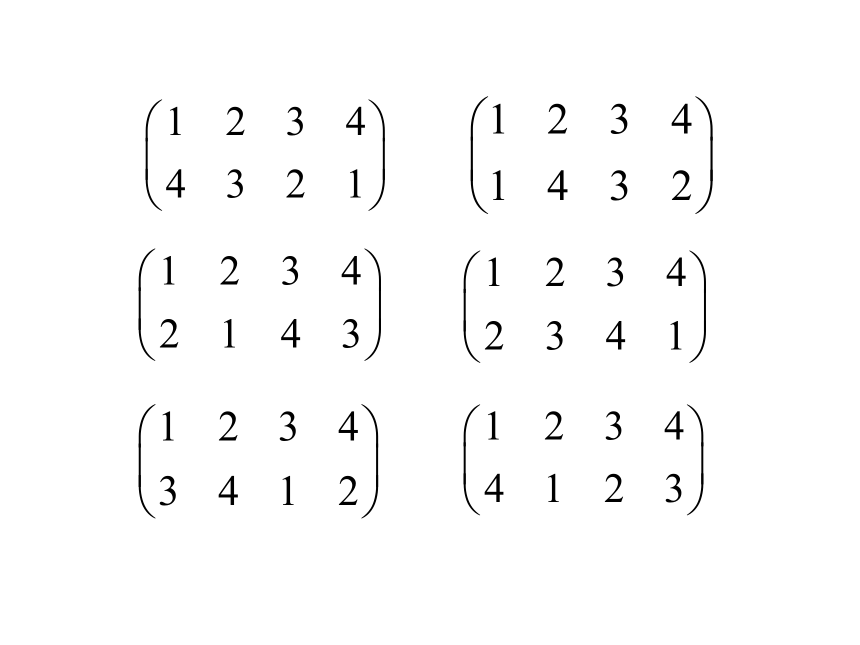

文档简介
(共31张PPT)
在上一讲,我们通过画图或操作模型的方法,研究了正三角形的对称群(D3, )以及正方形的对称群(D4, ).回想一下群的定义和它的性质.
在上一节,我们用群的方法来表示正n边形的对称变换,那么除了它自身的对称群以外,还有没有其他的对称变换?这一讲我们将考察代数学中的对称.
2.1 n元对称群Sn
感知图形对称变换的特点.
掌握n元对称群的概念.
掌握两个置换的合成运算.
通过观察、操作,了解变换的过程.
进一步掌握对称变换.
通过实例,学习置换的合成运算.
让学生从前后对比中掌握所学知识.
从实例中掌握解题思路.
培养合作交流意识.
置换的表达形式.
置换的合成运算.
n元对称群的概念.
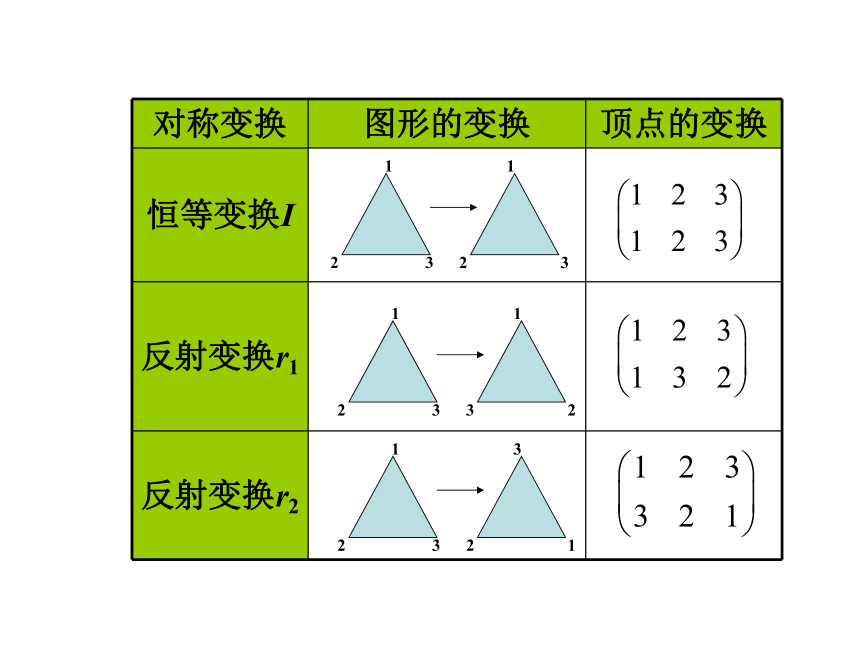
前面我们曾经讨论过,正n边形的对称变换保持它的对称中心不动,而把它的n个顶点仍然映成顶点.所以,正n边形的对称变换可以用在对称变换的作用下相应顶点的变换来表示.
例如,下表列出了正三角形的对称变换、相应图形的变换和相应顶点的变换.
1
1
2
2
3
3
1
1
2
3
2
3
1
3
2
2
1
3
对称变换 图形的变换 顶点的变换
恒等变换I
反射变换r1
反射变换r2
1
2
2
1
3
3
1
3
2
1
2
3
1
2
2
3
1
3
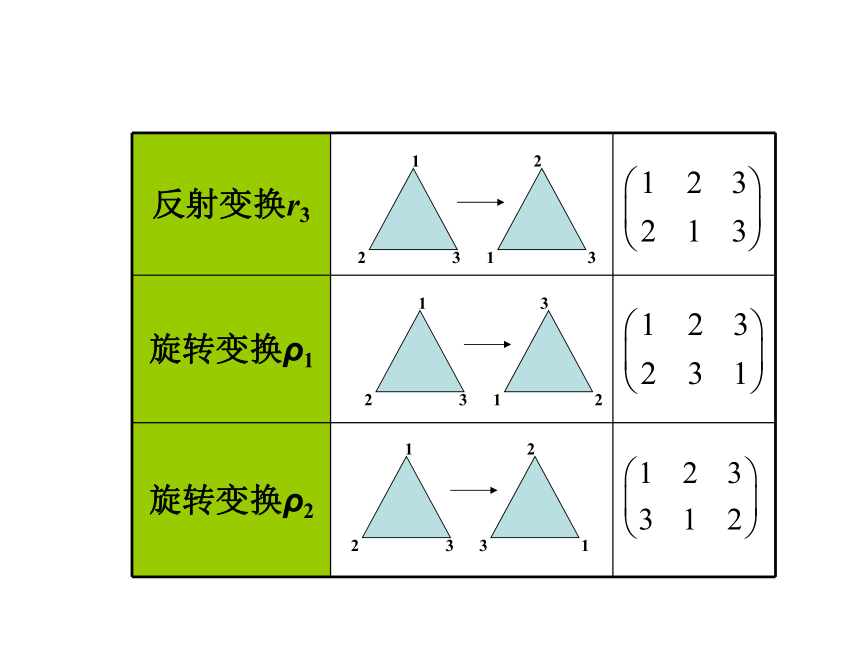
反射变换r3
旋转变换ρ1
旋转变换ρ2
类似地,正方形的对称变换也可以用数字1,2,3,4的相应置换来表示:
置换这种表示不仅仅是一种符号,实际上定义了集合{1,2,3,...,n}(n∈N*)到自身的一个一一对应.1,2,...,n这n个数的每一个置换都确定了集合{1,2,3,...,n}到其自身的一个一一对应.
例如,正三角形的对称变换所对应的置换是集合T3={1,2,3}到其自身的一一对应,它们共有2 3=6个,这是T3的全部置换.T3的全部置换组成的集合记作S3.
正方形的对称变换所对应的置换是集合T4={1,2,3,4}到其自身的一一对应,它们共有2×4=8个,但这只是T4的部分置换.容易知道,T4共有4!=24个置换.T4的全部置换组成的集合记作S4.
例:写出集合T4={1,2,3,4}的所有置换.
解:我们先用排序的方法写出T4所有的排列:
当置换第一行的顺序固定为1,2,3,4的时候,每一个排列就对应了一个置换.所以这24个置换是:
与对称变换的合成相对应,我们可以定义置换的合成.通常两个置换的合成也是按照从右到左的顺序,先做一个置换,再做一个置换.
例如,
与
的合
成记作
?
,由于
表示的对应是
1 2 3 4
1 4 3 2
表示的对应是
1 2 3 4
2 1 4 3
我们规定,
?
表示的对应是
1 2 3 4
1 4 3 2
2 3 4 1
所以,
?
可见,两个置换的合成也是一个替换,而且等于两个相应对称变换的合成所对应的置换.
像
这样,
把各数字都对应到它本身的置换称为恒等置换.若两个置换a,b的合成等于恒等置换,即有 ,那么我们称a,b互为逆置换.
例: 求下列两个置换的合成.
解:
由本例题可以知道,置换的合成不满足交换律.
有了上面的准备,我们就能用置换来表示二面体群(Dn,?)了.
以正三角形为例,把正三角形的6个置换组成的集合仍然记作D3,把置换之间的合成“?”看作D3上的一种运算,那么通过计算可以得到下述D3的乘法表.
?
由上表容易验证下述4条是成立的:
Ⅰ.对任意的m1,m2∈D3,m1?m2∈D3;
Ⅱ.D3中存在恒等置换,满足对任意的m∈D3,I?m=m?I=m;
Ⅲ.对任意的m∈D3,存在置换m?∈D3,使得m?m?=I=m??m;
Ⅳ.对任意的m1,m2,m3∈D3,m3?(m2?m1)=(m3?m2) ?m1.
我们把置换集合D3连同它上面的运算“?”也称为对称群(D3,?),这是正三角形的对称群的另外一种表达方式.
类似地,可以用置换表示正方形,正五边形,正六边形......正n边形的对称群,从而得到二面体群(Dn,?)(n≥3)的另外一种表示方式.
一般地,Tn={1,2,...,n}共有n!个置换,它们组成的集合记作Sn.如果把置换之间的合成“?”看作Tn上的一种运算,可以证明,下述4条是成立的.
Ⅰ.Sn中任意两个置换合成的结果仍然在Sn中;
Ⅱ.Sn中存在恒等置换;
Ⅲ.Sn中任意一个置换的逆置换仍然在Sn中;
Ⅳ.Sn中置换的合成满足结合律.
因此,(Sn,?)是Tn的对称群,称为n元对称群.
1. n元对称群Sn的定义
2. 对称变换的置换表示
3. 置换的合成运算
在上一讲,我们通过画图或操作模型的方法,研究了正三角形的对称群(D3, )以及正方形的对称群(D4, ).回想一下群的定义和它的性质.
在上一节,我们用群的方法来表示正n边形的对称变换,那么除了它自身的对称群以外,还有没有其他的对称变换?这一讲我们将考察代数学中的对称.
2.1 n元对称群Sn
感知图形对称变换的特点.
掌握n元对称群的概念.
掌握两个置换的合成运算.
通过观察、操作,了解变换的过程.
进一步掌握对称变换.
通过实例,学习置换的合成运算.
让学生从前后对比中掌握所学知识.
从实例中掌握解题思路.
培养合作交流意识.
置换的表达形式.
置换的合成运算.
n元对称群的概念.
前面我们曾经讨论过,正n边形的对称变换保持它的对称中心不动,而把它的n个顶点仍然映成顶点.所以,正n边形的对称变换可以用在对称变换的作用下相应顶点的变换来表示.
例如,下表列出了正三角形的对称变换、相应图形的变换和相应顶点的变换.
1
1
2
2
3
3
1
1
2
3
2
3
1
3
2
2
1
3
对称变换 图形的变换 顶点的变换
恒等变换I
反射变换r1
反射变换r2
1
2
2
1
3
3
1
3
2
1
2
3
1
2
2
3
1
3
反射变换r3
旋转变换ρ1
旋转变换ρ2
类似地,正方形的对称变换也可以用数字1,2,3,4的相应置换来表示:
置换这种表示不仅仅是一种符号,实际上定义了集合{1,2,3,...,n}(n∈N*)到自身的一个一一对应.1,2,...,n这n个数的每一个置换都确定了集合{1,2,3,...,n}到其自身的一个一一对应.
例如,正三角形的对称变换所对应的置换是集合T3={1,2,3}到其自身的一一对应,它们共有2 3=6个,这是T3的全部置换.T3的全部置换组成的集合记作S3.
正方形的对称变换所对应的置换是集合T4={1,2,3,4}到其自身的一一对应,它们共有2×4=8个,但这只是T4的部分置换.容易知道,T4共有4!=24个置换.T4的全部置换组成的集合记作S4.
例:写出集合T4={1,2,3,4}的所有置换.
解:我们先用排序的方法写出T4所有的排列:
当置换第一行的顺序固定为1,2,3,4的时候,每一个排列就对应了一个置换.所以这24个置换是:
与对称变换的合成相对应,我们可以定义置换的合成.通常两个置换的合成也是按照从右到左的顺序,先做一个置换,再做一个置换.
例如,
与
的合
成记作
?
,由于
表示的对应是
1 2 3 4
1 4 3 2
表示的对应是
1 2 3 4
2 1 4 3
我们规定,
?
表示的对应是
1 2 3 4
1 4 3 2
2 3 4 1
所以,
?
可见,两个置换的合成也是一个替换,而且等于两个相应对称变换的合成所对应的置换.
像
这样,
把各数字都对应到它本身的置换称为恒等置换.若两个置换a,b的合成等于恒等置换,即有 ,那么我们称a,b互为逆置换.
例: 求下列两个置换的合成.
解:
由本例题可以知道,置换的合成不满足交换律.
有了上面的准备,我们就能用置换来表示二面体群(Dn,?)了.
以正三角形为例,把正三角形的6个置换组成的集合仍然记作D3,把置换之间的合成“?”看作D3上的一种运算,那么通过计算可以得到下述D3的乘法表.
?
由上表容易验证下述4条是成立的:
Ⅰ.对任意的m1,m2∈D3,m1?m2∈D3;
Ⅱ.D3中存在恒等置换,满足对任意的m∈D3,I?m=m?I=m;
Ⅲ.对任意的m∈D3,存在置换m?∈D3,使得m?m?=I=m??m;
Ⅳ.对任意的m1,m2,m3∈D3,m3?(m2?m1)=(m3?m2) ?m1.
我们把置换集合D3连同它上面的运算“?”也称为对称群(D3,?),这是正三角形的对称群的另外一种表达方式.
类似地,可以用置换表示正方形,正五边形,正六边形......正n边形的对称群,从而得到二面体群(Dn,?)(n≥3)的另外一种表示方式.
一般地,Tn={1,2,...,n}共有n!个置换,它们组成的集合记作Sn.如果把置换之间的合成“?”看作Tn上的一种运算,可以证明,下述4条是成立的.
Ⅰ.Sn中任意两个置换合成的结果仍然在Sn中;
Ⅱ.Sn中存在恒等置换;
Ⅲ.Sn中任意一个置换的逆置换仍然在Sn中;
Ⅳ.Sn中置换的合成满足结合律.
因此,(Sn,?)是Tn的对称群,称为n元对称群.
1. n元对称群Sn的定义
2. 对称变换的置换表示
3. 置换的合成运算
