高中数学人教新课标A版选修3-4第三讲对称与群的故事3.2 化学分子的对称群(共33张PPT)
文档属性
| 名称 | 高中数学人教新课标A版选修3-4第三讲对称与群的故事3.2 化学分子的对称群(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 771.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 22:25:34 | ||
图片预览










文档简介
(共33张PPT)
物体的形状往往具有这样那样的“对称性”.例如雪花、树叶.
由于物体是由分子构成的,因此可以猜想,分子也会有这样那样的对称性,而且这种对称性往往在很大程度上能够决定分子的性质.
感知分子的对称特点.
掌握对称面和真轴的概念.
通过观察了解分子的对称变换.
进一步掌握对称变换.
让学生从前后对比中掌握所学知识.
从实例中掌握抽象的概念.
培养合作交流意识.
对称面和真轴的概念.
现实中群给化学研究带来的方便性.
数学概念的抽象性.
在化学分子的研究中,对于其对称性的研究常常可以使人加深对物体性质的认识.
人们有时会说一些分子比另一些分子更对称,或者某些分子具有高度对称性,某些分子具有低对称性.
虽然从直观上看,这些说法都是明确的,但是为了建立严格的分子对称性的概念,科学家们使用了群这一数学工具.
这里,我们以水分子H2O和氨气分子NH3为例,介绍化学分子的对称变换和对称群.
水分子H2O是由一个氧原子O和2个氢原子H构成,并且这3个原子在同一个平面内.
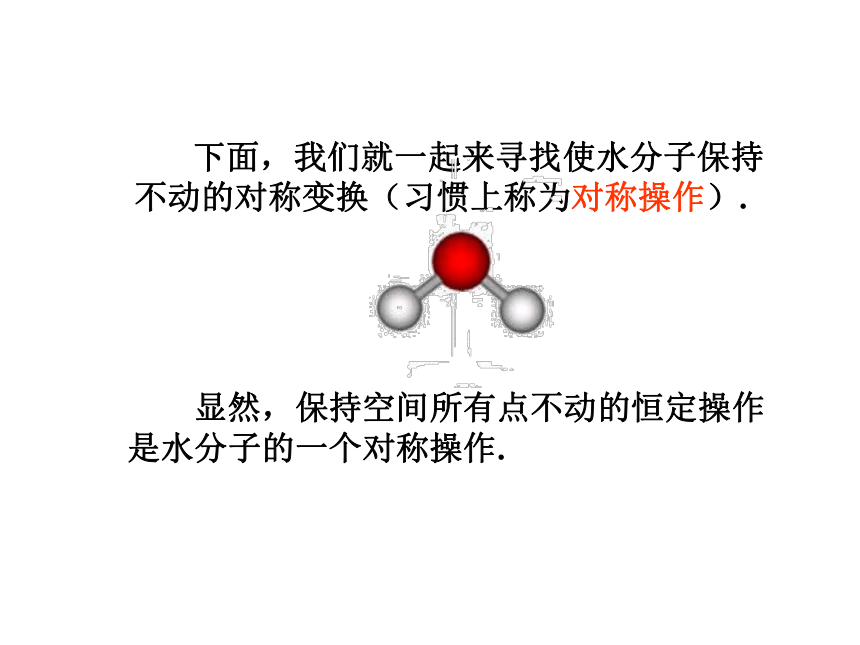
下面,我们就一起来寻找使水分子保持不动的对称变换(习惯上称为对称操作).
显然,保持空间所有点不动的恒定操作是水分子的一个对称操作.
接着考虑水分子的反射变换.与平面图形不同,这里研究的反射变换总是与对称面联系在一起的.
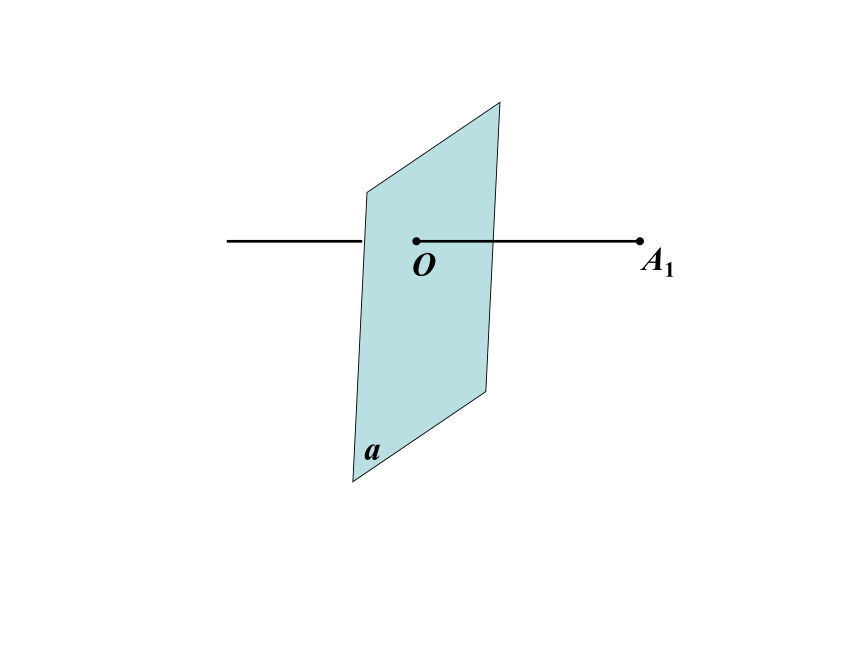
如下图,平面a⊥线段AA1,且过线段AA1的中心O,这时,交换A,A1的位置,得到的线段与原来的线段重合,我们称a平面为线段AA1的对称面.
a
A1
O
同样地,我们可以用这样的对称操作来定义分子的对称面.从每个原子向一个平面作垂线,把垂线向平面的反面延长相等的距离,并把原子移到垂线的另一端,如果分子的所有原子都完成了这种操作后,仍与原来的分子重合,我们就称这个平面是这个分子的一个对称面.
观察H2O的模型,容易发现它有两个对称面.
如下图,分子所在的平面就是一个对称面.经过关于这个平面的反射,所有的原子都保持不动.
如下图,包含氧原子并垂直于分子所在平面的平面也是一个对称面,经过这个对称面的反射,氧原子保持不动,而两个氢原子交换位置.
再考虑选择变换.这里的旋转变换是绕一条直线的旋转,这条直线称为真轴.
经过试验,可以发现H2O只有一条真轴,即通过氧原子并平分氢原子连线的直线.将水分子绕真轴旋转180°后,它仍与原来的分子重合.如下图.
这样,我们就找到了H2O的4个对称操作:
(1)恒等操作;
(2)关于2个对称面的2个反射;
(3)绕1条真轴的旋转.
事实上,这4个对称操作组成的集合包含了H2O的全部对称操作.两个对称操作的合成(即先做一个对称操作,再做另一个对称操作)就是这个集合上的一个二元运算.请同学们自己验证它们构成了H2O的对称群(通常记作C2v).
再来看氨分子NH3,它由一个氮原子N和3个氢原子H构成,整个分子呈正三角锥型,3个氢原子H在同一个平面内.如下图.
由氨分子的结构可以看出,NH3有3个对称面,每个对称面都包含氮原子和1个氢原子,并平分其他2个氢原子的连线.还有1条真轴,即通过氮原子并垂直于3个氢原子所在平面的直线.
这样,氨分子就有6个对称操作.
恒等操作:
绕真轴旋转120°:
绕真轴旋转240°:
关于对称面α的反射:
关于对称面β的反射:
关于对称面γ的反射:
同水分子的对称操作一样,氨分子的这6个对称操作,就是NH3的全部对称操作,它们组成的集合连同对称操作的合成构成了NH3的对称群(通常记作C3v).
数学上对于群的研究,并不关心群中的元素是什么,这些元素有什么物理意义.但当把群的基本理论与化学分子的具体对称性结合起来之后,群论就成了研究分子运动规律的一种有力的工具.
例如,化学家利用群论推导出具有各种各样几何构型的化学分子的对称群仅有32种;又如在利用群论分析分子对称性如何制约其量子力学解时,常常无需详细计算就能获得一些定性的结论.
本节主要从数学的角度,描述的化学分子的对称性.使同学们感受到数学概念的抽象性,它不指出具体的物理意义,而是注重元素的特点.这也正是数学的一般性.
物体的形状往往具有这样那样的“对称性”.例如雪花、树叶.
由于物体是由分子构成的,因此可以猜想,分子也会有这样那样的对称性,而且这种对称性往往在很大程度上能够决定分子的性质.
感知分子的对称特点.
掌握对称面和真轴的概念.
通过观察了解分子的对称变换.
进一步掌握对称变换.
让学生从前后对比中掌握所学知识.
从实例中掌握抽象的概念.
培养合作交流意识.
对称面和真轴的概念.
现实中群给化学研究带来的方便性.
数学概念的抽象性.
在化学分子的研究中,对于其对称性的研究常常可以使人加深对物体性质的认识.
人们有时会说一些分子比另一些分子更对称,或者某些分子具有高度对称性,某些分子具有低对称性.
虽然从直观上看,这些说法都是明确的,但是为了建立严格的分子对称性的概念,科学家们使用了群这一数学工具.
这里,我们以水分子H2O和氨气分子NH3为例,介绍化学分子的对称变换和对称群.
水分子H2O是由一个氧原子O和2个氢原子H构成,并且这3个原子在同一个平面内.
下面,我们就一起来寻找使水分子保持不动的对称变换(习惯上称为对称操作).
显然,保持空间所有点不动的恒定操作是水分子的一个对称操作.
接着考虑水分子的反射变换.与平面图形不同,这里研究的反射变换总是与对称面联系在一起的.
如下图,平面a⊥线段AA1,且过线段AA1的中心O,这时,交换A,A1的位置,得到的线段与原来的线段重合,我们称a平面为线段AA1的对称面.
a
A1
O
同样地,我们可以用这样的对称操作来定义分子的对称面.从每个原子向一个平面作垂线,把垂线向平面的反面延长相等的距离,并把原子移到垂线的另一端,如果分子的所有原子都完成了这种操作后,仍与原来的分子重合,我们就称这个平面是这个分子的一个对称面.
观察H2O的模型,容易发现它有两个对称面.
如下图,分子所在的平面就是一个对称面.经过关于这个平面的反射,所有的原子都保持不动.
如下图,包含氧原子并垂直于分子所在平面的平面也是一个对称面,经过这个对称面的反射,氧原子保持不动,而两个氢原子交换位置.
再考虑选择变换.这里的旋转变换是绕一条直线的旋转,这条直线称为真轴.
经过试验,可以发现H2O只有一条真轴,即通过氧原子并平分氢原子连线的直线.将水分子绕真轴旋转180°后,它仍与原来的分子重合.如下图.
这样,我们就找到了H2O的4个对称操作:
(1)恒等操作;
(2)关于2个对称面的2个反射;
(3)绕1条真轴的旋转.
事实上,这4个对称操作组成的集合包含了H2O的全部对称操作.两个对称操作的合成(即先做一个对称操作,再做另一个对称操作)就是这个集合上的一个二元运算.请同学们自己验证它们构成了H2O的对称群(通常记作C2v).
再来看氨分子NH3,它由一个氮原子N和3个氢原子H构成,整个分子呈正三角锥型,3个氢原子H在同一个平面内.如下图.
由氨分子的结构可以看出,NH3有3个对称面,每个对称面都包含氮原子和1个氢原子,并平分其他2个氢原子的连线.还有1条真轴,即通过氮原子并垂直于3个氢原子所在平面的直线.
这样,氨分子就有6个对称操作.
恒等操作:
绕真轴旋转120°:
绕真轴旋转240°:
关于对称面α的反射:
关于对称面β的反射:
关于对称面γ的反射:
同水分子的对称操作一样,氨分子的这6个对称操作,就是NH3的全部对称操作,它们组成的集合连同对称操作的合成构成了NH3的对称群(通常记作C3v).
数学上对于群的研究,并不关心群中的元素是什么,这些元素有什么物理意义.但当把群的基本理论与化学分子的具体对称性结合起来之后,群论就成了研究分子运动规律的一种有力的工具.
例如,化学家利用群论推导出具有各种各样几何构型的化学分子的对称群仅有32种;又如在利用群论分析分子对称性如何制约其量子力学解时,常常无需详细计算就能获得一些定性的结论.
本节主要从数学的角度,描述的化学分子的对称性.使同学们感受到数学概念的抽象性,它不指出具体的物理意义,而是注重元素的特点.这也正是数学的一般性.
