高中数学人教新课标A版选修3-4第三讲对称与群的故事3.3 晶体的分类(共22张PPT)
文档属性
| 名称 | 高中数学人教新课标A版选修3-4第三讲对称与群的故事3.3 晶体的分类(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 22:29:56 | ||
图片预览







文档简介
(共22张PPT)
晶体是原子、离子或分子按照一定的周期性,在结晶过程中,在空间排列形成具有一定规则的几何外形的固体.
晶体的概念:
在自然界中,几何对称最突出地表现在晶体中.对晶体的分类有化学的,也有物理的,这里主要从群的角度去考虑晶体的分类分类问题.
感知分子的对称特点.
掌握对称面和真轴的概念.
通过观察了解分子的对称变换.
进一步掌握对称变换.
让学生从前后对比中掌握所学知识.
从实例中掌握抽象的概念.
培养合作交流意识.
对称面和真轴的概念.
现实中群给化学研究带来的方便性.
数学概念的抽象性.
晶体的对称是极其精巧的,例如下图是食盐(NaCl):
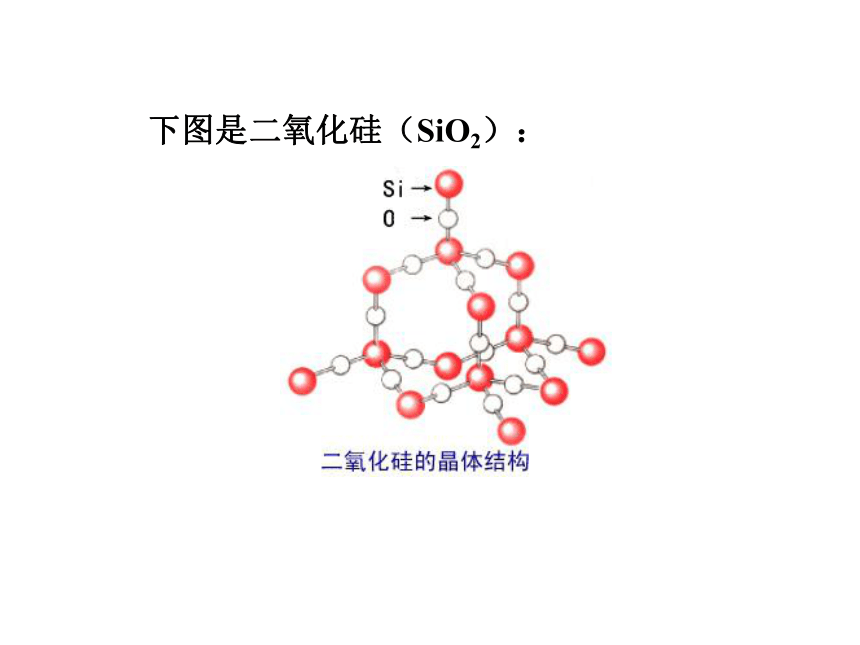
下图是二氧化硅(SiO2):
下图是二氧化钛(TiO2):
晶体可以看成由空间单位格点(晶体原子在平衡位置时组成的空间中一个有规则的多面体)经过不在同一平面内的三组平移生成的空间格点.晶体几何形状的多样性需要有一中能描述其对称性规律的统一的表述模式,这就是群.
在19世纪后半叶,科学家们发现晶体外形的全部对称形式,也就是使单位格点保持不动的对称群(通常称为对称点群),共有32种;而晶体内部构造的一切可能的对称形式,也就是使空间格点不动对称群(通常称为空间群),共有230种.
32种对称点群刻画了晶体外形所呈现得全部对称关系.而晶体的物理对称性除了外形所显示的,更多的是由其内部原子的排列揭示的,230种空间群刻画了晶体内部原子及离子间全部的对称关系.
正如在二维空间中,带饰群和面饰群在平面装饰艺术中起到了非常重要的作用一样,对称点群和空间群使得晶体学中的一些重要问题得到了透彻而深入的解释.这一点可以从历史上晶体结构的发现过程得到证明.
1912年,年轻的德国物理学家劳厄(Max von Laue)首次用较窄的X射线照射某个晶体,并在晶体的后面放置照相胶卷,结果发现X射线被单位晶格转向,在胶卷上以点的形式出现.
如下图.
这些二维图像具有重要的意义,从图中我们可以看出,晶体的对称性被忠实地表现出来了.后来,矿物学家都是通过研究晶体的内部结构的.通常,投影钟所呈现的是二面晶体群D4,D6,D8,D12等.
这里简单介绍一下劳厄
劳厄,M.von Max von Laue (1879~1960) 德国物理学家,X射线晶体分析的先驱1879年10月5日生于柯布伦茨附近的普法芬多夫,1960年4月23日在柏林逝世.
劳厄第一个用晶体作光栅,发现了X射线的衍射现象,从而既证明了晶体的点阵结构,又证明了X射线是一种光波.他因此荣获了1914年度诺贝尔物理学奖.在这一重大发现的背后,晶体对称群的理论起了关键性作用.
随后不久,两位英国科学家布拉格父子(William Henry Bragg和他的22岁的儿子William Lawrence Bragg)用劳厄的衍射点和空间群的知识计算出了晶体中原子的固有排列形状,这一发现标志着现代矿物学的诞生.1915年,布拉格父子被授予诺贝尔物理学奖.
最后简单介绍一下诺贝尔奖.
诺贝尔奖是以瑞典著名化学家、硝化甘油炸药发明人阿尔弗雷德·贝恩哈德·诺贝尔(Alfred Bernhard Nobel, 1833.10.21--1896.12.10)的部分遗产作为基金创立的.诺贝尔奖包括金质奖章、证书和奖金支票.
本节通过从晶体的角度,来认识群在自然界的存在,以及群理论在现实世界的应用.
晶体是原子、离子或分子按照一定的周期性,在结晶过程中,在空间排列形成具有一定规则的几何外形的固体.
晶体的概念:
在自然界中,几何对称最突出地表现在晶体中.对晶体的分类有化学的,也有物理的,这里主要从群的角度去考虑晶体的分类分类问题.
感知分子的对称特点.
掌握对称面和真轴的概念.
通过观察了解分子的对称变换.
进一步掌握对称变换.
让学生从前后对比中掌握所学知识.
从实例中掌握抽象的概念.
培养合作交流意识.
对称面和真轴的概念.
现实中群给化学研究带来的方便性.
数学概念的抽象性.
晶体的对称是极其精巧的,例如下图是食盐(NaCl):
下图是二氧化硅(SiO2):
下图是二氧化钛(TiO2):
晶体可以看成由空间单位格点(晶体原子在平衡位置时组成的空间中一个有规则的多面体)经过不在同一平面内的三组平移生成的空间格点.晶体几何形状的多样性需要有一中能描述其对称性规律的统一的表述模式,这就是群.
在19世纪后半叶,科学家们发现晶体外形的全部对称形式,也就是使单位格点保持不动的对称群(通常称为对称点群),共有32种;而晶体内部构造的一切可能的对称形式,也就是使空间格点不动对称群(通常称为空间群),共有230种.
32种对称点群刻画了晶体外形所呈现得全部对称关系.而晶体的物理对称性除了外形所显示的,更多的是由其内部原子的排列揭示的,230种空间群刻画了晶体内部原子及离子间全部的对称关系.
正如在二维空间中,带饰群和面饰群在平面装饰艺术中起到了非常重要的作用一样,对称点群和空间群使得晶体学中的一些重要问题得到了透彻而深入的解释.这一点可以从历史上晶体结构的发现过程得到证明.
1912年,年轻的德国物理学家劳厄(Max von Laue)首次用较窄的X射线照射某个晶体,并在晶体的后面放置照相胶卷,结果发现X射线被单位晶格转向,在胶卷上以点的形式出现.
如下图.
这些二维图像具有重要的意义,从图中我们可以看出,晶体的对称性被忠实地表现出来了.后来,矿物学家都是通过研究晶体的内部结构的.通常,投影钟所呈现的是二面晶体群D4,D6,D8,D12等.
这里简单介绍一下劳厄
劳厄,M.von Max von Laue (1879~1960) 德国物理学家,X射线晶体分析的先驱1879年10月5日生于柯布伦茨附近的普法芬多夫,1960年4月23日在柏林逝世.
劳厄第一个用晶体作光栅,发现了X射线的衍射现象,从而既证明了晶体的点阵结构,又证明了X射线是一种光波.他因此荣获了1914年度诺贝尔物理学奖.在这一重大发现的背后,晶体对称群的理论起了关键性作用.
随后不久,两位英国科学家布拉格父子(William Henry Bragg和他的22岁的儿子William Lawrence Bragg)用劳厄的衍射点和空间群的知识计算出了晶体中原子的固有排列形状,这一发现标志着现代矿物学的诞生.1915年,布拉格父子被授予诺贝尔物理学奖.
最后简单介绍一下诺贝尔奖.
诺贝尔奖是以瑞典著名化学家、硝化甘油炸药发明人阿尔弗雷德·贝恩哈德·诺贝尔(Alfred Bernhard Nobel, 1833.10.21--1896.12.10)的部分遗产作为基金创立的.诺贝尔奖包括金质奖章、证书和奖金支票.
本节通过从晶体的角度,来认识群在自然界的存在,以及群理论在现实世界的应用.
