人教版高中数学必修4 2.1平面向量的实际背景及基本概念(共34张PPT)
文档属性
| 名称 | 人教版高中数学必修4 2.1平面向量的实际背景及基本概念(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
2.1平面向量的实际背景及基本概念
人教版高中数学必修四第二章平面向量
向量是近代数学中重要和基本的数学概念之一,有深刻的几何背景,是解决几何问题的有力工具。向量概念引入后,全等和平行(平移)、相似、垂直、勾股定理就可转化为向量的加(减)法、数乘向量、数量积运算,从而把图形的基本性质转化为向量的运算体系。
向量是沟通代数、几何与三角函数的一种工具,有着极其丰富的实际背景。在本章中,学生将了解向量丰富的实际背景,理解平面向量及其运算的意义,能用向量语言和方法表述和解决数学和物理中的一些问题,发展运算能力和解决实际问题的能力
2.1.1 向量的物理背景与概念
2.1.2 向量的几何表示
2.1.3 相等向量与共线向量
目标定位
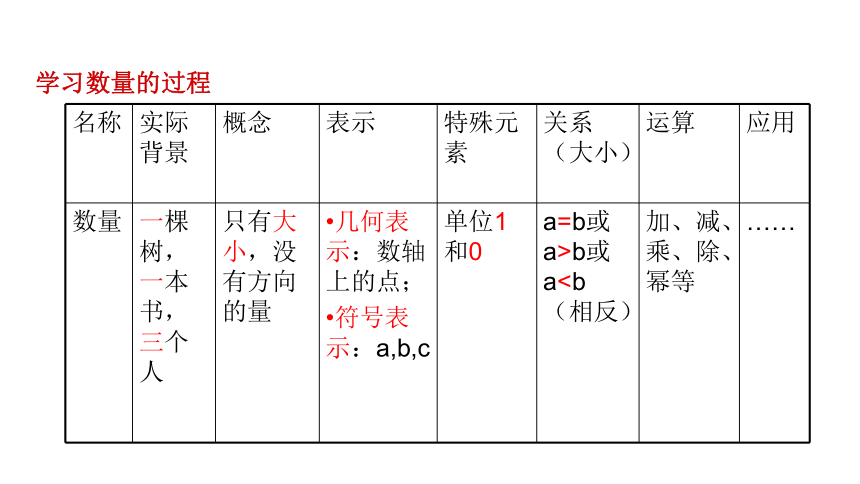
学习数量的过程
名称 实际背景 概念 表示 特殊元素 关系(大小) 运算 应用
数量 一棵树,一本书,三个人 只有大小,没有方向的量 几何表示:数轴上的点;
符号表示:a,b,c
单位1和0 a=b或a>b或a ……
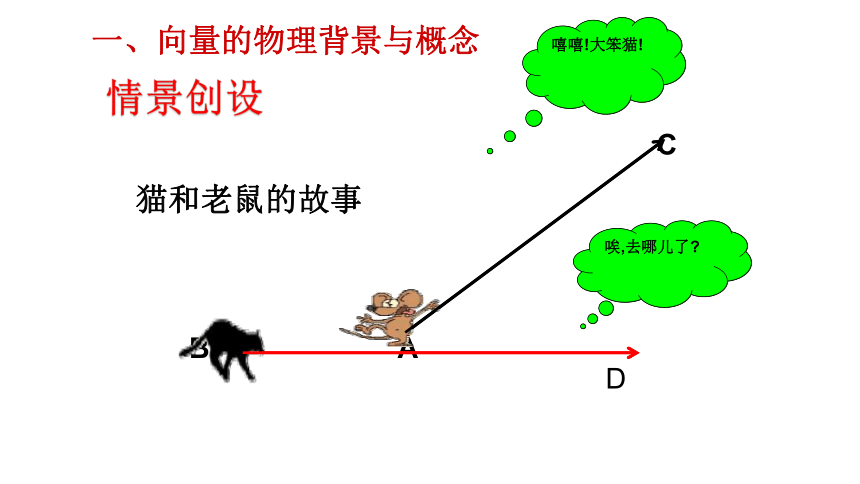
情景创设
猫和老鼠的故事
唉,去哪儿了?
嘻嘻!大笨猫!
A
B
C
D
唉,去哪儿了?
嘻嘻!大笨猫!
一、向量的物理背景与概念
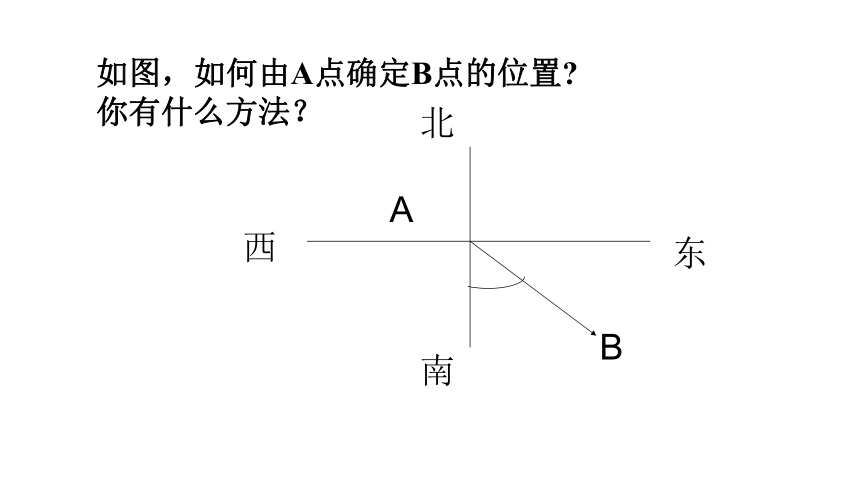
如图,如何由A点确定B点的位置?
你有什么方法?
北
西
东
南
A
B
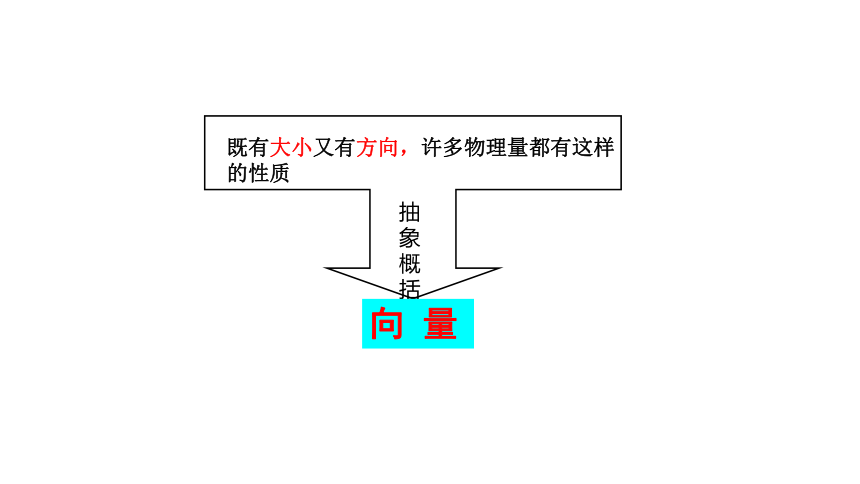
既有大小又有方向,许多物理量都有这样的性质
抽象概括
向 量
向量:既有大小,又有方向的量.
1.问:力、速度、加速度、位移有什么共同特点?
2.问:路程、面积、功、身高
数量:只有大小,没有方向的量.
2.1.1 向量的物理背景与概念
向量:既有大小,又有方向的量.
1.问:力、速度、加速度、位移有什么共同特点?
2.问:路程、面积、功、身高
2.1.1 向量的物理背景与概念
数量:只有大小,没有方向的量.
向量:既有大小,又有方向的量.
1.问:力、速度、加速度、位移有什么共同特点?
2.问:路程、面积、功、身高
2.1.1 向量的物理背景与概念
向量:既有大小,又有方向的量.
1.问:力、速度、加速度、位移有什么共同特点?
2.问:路程、面积、功、身高
数量:只有大小,没有方向的量.
向量的两要素:方向、大小
2.1.1 向量的物理背景与概念
向量:既有大小,又有方向的量.
1.问:力、速度、加速度、位移有什么共同特点?
2.问:路程、面积、功、身高
向量的两要素:方向、大小
向量的两要素:方向、大小
在数学中,把既有大小,又有方向的量叫做向量.
在数学中,把只有大小,没有方向的量叫做数量.
①数量只有大小,是一个代数量,可以进行代数运算、比较大小.
②向量有方向,大小双重属性,而方向是不能比较大小的,因此向量不能比较大小。
注:向量与数量的区别
二、向量的概念
在数学中,把既有大小,又有方向的量叫做向量.
在数学中,把只有大小,没有方向的量叫做数量.
①数量只有大小,是一个代数量,可以进行代数运算、比较大小.
②向量有方向,大小双重属性,而方向是不能比较大小的,因此向量不能比较大小。
注:向量与数量的区别
二、向量的概念
注:我们所学的向量常被称为自由向量.
2.1.2 向量的表示
1、有向线段的三要素:起点、方向、长度
A(起点)
B(终点)
2、向量的表示
(1)向量的几何表示:可以用有向线段表示.
(2)向量的符号表示:① , , , . . .印刷体可以用黑体表示向量。② ,
向量就是有向线段么?
单位向量
零向量
:长度等于1个单位的向量叫做单位向量.
:长度为0的向量叫做零向量,记作 0.
注:零向量也有方向,并且规定零向量的方向是任意的
注:单位向量的大小相等,但方向不一定相同.
向量的模和两个特殊的向量
注:向量的模是可以比较大小的。
就是向量 的模,
向量 的 长度(大小)
记作
模
(1)数量和向量都可以比较大小吗?
(2)向量的模是一个正数吗?
(3)所有单位向量的模都相等?
(4)书写向量符号时箭头可以省吗?
课堂反馈
规定0 向量与任一向量平行
2.相等向量:长度相等且方向相同的向量叫做相等向量。
记作: a = b
b
a
2.1.3 相等向量和平行向量(共线)
1.平行向量:方向相同或相反的非零向量
a
b
c
记作: a b c
共线向量
平行向量 相反向量
任意一组平行向量都可以平移到同一直线上,所平行向量也叫共线向量
任意一个向量 AB 的相反向量 BA
(1)相等向量一定是平行向量?
(2)平行向量一定是相等向量?
练习
在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等。
(2)与向量 长度相等的向量
有多少个?
例3.如图,设 是正六边形 的中心,分别写出图中
与向量 、 、 相等的向量.
(3)与向量 共线的向量有
哪几个?
练习∶上题中
(1)向量OA与FE相等吗?
F
E
A
C
B
D
O
O
判断下列命题是否正确,若不正确,请简述理由.
1、任一向量与它的相反向量不相等;
2、共线的向量,若起点不同,则终点一定不同.
3、①平行向量是否一定方向相同?
②不相等的向量是否一定不平行?
③与零向量相等的向量必定是什么向量?
④与任意向量都平行的向量是什么向量?
⑤若两个向量在同一直线上,则这两个向量一定是什么向量?
⑥共线向量一定在同一直线上吗?
练习:
1.与非零向量a平行的向量中,不相等的单位向量有_____个.
练习:
1.已知a、b为不共线的非零向量,且存在向量 c,使 c ∥ a, c ∥ b, 则
c =____
练习:判断正误
对于向量a , b
(1)若“│a│=│b│”,则“ a = b ” ( )
(2)若“a = b ”,则“│a│=│b│ ” ( )
在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等。
练习
1、若两个向量在同一直线上,则这两个向量是什么向量?
2、共线向量一定在一条直线上吗?
练习:
在质量、重力、速度、加速度、身高、面积、体积这些量中,哪些是数量?哪些是向量?
数量有:
向量有:
练习:
在质量、重力、速度、加速度、身高、面积、体积这些量中,哪些是数量?哪些是向量?
数量有:质量、身高、面积、体积
向量有:重力、速度、加速度
练习:
1、单位向量是否一定相等?
2、单位向量的大小是否一定相等?
练习:
1、单位向量是否一定相等?
2、单位向量的大小是否一定相等?
不一定
一定
练习:
1、平行向量是否一定方向相同?
2、不相等的向量一定不平行吗?
练习:
1、平行向量是否一定方向相同?
2、不相等的向量一定不平行吗?
不一定
不一定
当堂测试
1、下列物理量中, 不能称为向量的是 ( )
A.距离 B.加速度 C.力 D.位移
2、下列四个命题正确的是 ( )
A.两个单位向量一定相等 B.若与不共线,则与都是非零向量
C.共线的单位向量必相等 D.两个相等的向量起点、方向、长度必须都相同
3、下列说法错误的是 ( )
A.向量的长度与向量的长度相等 B.零向量与任意非零向量平行
C.长度相等方向相反的向量共线 D.方向相反的向量可能相等
4、对于以下命题:(1)平行向量一定相等; (2)不相等的向量一定不平行;
(3)共线向量一定相等;(4)相等向量一定共线。其中真命题的个数是 ( )
A.0个 B.1个 C.2个 D.3个
相等向量
零向量
单位向量
平行向量
共线向量
向量的方向
向量的大小
(长度,模)
有向线段
向 量
课时小结
2.1平面向量的实际背景及基本概念
人教版高中数学必修四第二章平面向量
向量是近代数学中重要和基本的数学概念之一,有深刻的几何背景,是解决几何问题的有力工具。向量概念引入后,全等和平行(平移)、相似、垂直、勾股定理就可转化为向量的加(减)法、数乘向量、数量积运算,从而把图形的基本性质转化为向量的运算体系。
向量是沟通代数、几何与三角函数的一种工具,有着极其丰富的实际背景。在本章中,学生将了解向量丰富的实际背景,理解平面向量及其运算的意义,能用向量语言和方法表述和解决数学和物理中的一些问题,发展运算能力和解决实际问题的能力
2.1.1 向量的物理背景与概念
2.1.2 向量的几何表示
2.1.3 相等向量与共线向量
目标定位
学习数量的过程
名称 实际背景 概念 表示 特殊元素 关系(大小) 运算 应用
数量 一棵树,一本书,三个人 只有大小,没有方向的量 几何表示:数轴上的点;
符号表示:a,b,c
单位1和0 a=b或a>b或a
情景创设
猫和老鼠的故事
唉,去哪儿了?
嘻嘻!大笨猫!
A
B
C
D
唉,去哪儿了?
嘻嘻!大笨猫!
一、向量的物理背景与概念
如图,如何由A点确定B点的位置?
你有什么方法?
北
西
东
南
A
B
既有大小又有方向,许多物理量都有这样的性质
抽象概括
向 量
向量:既有大小,又有方向的量.
1.问:力、速度、加速度、位移有什么共同特点?
2.问:路程、面积、功、身高
数量:只有大小,没有方向的量.
2.1.1 向量的物理背景与概念
向量:既有大小,又有方向的量.
1.问:力、速度、加速度、位移有什么共同特点?
2.问:路程、面积、功、身高
2.1.1 向量的物理背景与概念
数量:只有大小,没有方向的量.
向量:既有大小,又有方向的量.
1.问:力、速度、加速度、位移有什么共同特点?
2.问:路程、面积、功、身高
2.1.1 向量的物理背景与概念
向量:既有大小,又有方向的量.
1.问:力、速度、加速度、位移有什么共同特点?
2.问:路程、面积、功、身高
数量:只有大小,没有方向的量.
向量的两要素:方向、大小
2.1.1 向量的物理背景与概念
向量:既有大小,又有方向的量.
1.问:力、速度、加速度、位移有什么共同特点?
2.问:路程、面积、功、身高
向量的两要素:方向、大小
向量的两要素:方向、大小
在数学中,把既有大小,又有方向的量叫做向量.
在数学中,把只有大小,没有方向的量叫做数量.
①数量只有大小,是一个代数量,可以进行代数运算、比较大小.
②向量有方向,大小双重属性,而方向是不能比较大小的,因此向量不能比较大小。
注:向量与数量的区别
二、向量的概念
在数学中,把既有大小,又有方向的量叫做向量.
在数学中,把只有大小,没有方向的量叫做数量.
①数量只有大小,是一个代数量,可以进行代数运算、比较大小.
②向量有方向,大小双重属性,而方向是不能比较大小的,因此向量不能比较大小。
注:向量与数量的区别
二、向量的概念
注:我们所学的向量常被称为自由向量.
2.1.2 向量的表示
1、有向线段的三要素:起点、方向、长度
A(起点)
B(终点)
2、向量的表示
(1)向量的几何表示:可以用有向线段表示.
(2)向量的符号表示:① , , , . . .印刷体可以用黑体表示向量。② ,
向量就是有向线段么?
单位向量
零向量
:长度等于1个单位的向量叫做单位向量.
:长度为0的向量叫做零向量,记作 0.
注:零向量也有方向,并且规定零向量的方向是任意的
注:单位向量的大小相等,但方向不一定相同.
向量的模和两个特殊的向量
注:向量的模是可以比较大小的。
就是向量 的模,
向量 的 长度(大小)
记作
模
(1)数量和向量都可以比较大小吗?
(2)向量的模是一个正数吗?
(3)所有单位向量的模都相等?
(4)书写向量符号时箭头可以省吗?
课堂反馈
规定0 向量与任一向量平行
2.相等向量:长度相等且方向相同的向量叫做相等向量。
记作: a = b
b
a
2.1.3 相等向量和平行向量(共线)
1.平行向量:方向相同或相反的非零向量
a
b
c
记作: a b c
共线向量
平行向量 相反向量
任意一组平行向量都可以平移到同一直线上,所平行向量也叫共线向量
任意一个向量 AB 的相反向量 BA
(1)相等向量一定是平行向量?
(2)平行向量一定是相等向量?
练习
在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等。
(2)与向量 长度相等的向量
有多少个?
例3.如图,设 是正六边形 的中心,分别写出图中
与向量 、 、 相等的向量.
(3)与向量 共线的向量有
哪几个?
练习∶上题中
(1)向量OA与FE相等吗?
F
E
A
C
B
D
O
O
判断下列命题是否正确,若不正确,请简述理由.
1、任一向量与它的相反向量不相等;
2、共线的向量,若起点不同,则终点一定不同.
3、①平行向量是否一定方向相同?
②不相等的向量是否一定不平行?
③与零向量相等的向量必定是什么向量?
④与任意向量都平行的向量是什么向量?
⑤若两个向量在同一直线上,则这两个向量一定是什么向量?
⑥共线向量一定在同一直线上吗?
练习:
1.与非零向量a平行的向量中,不相等的单位向量有_____个.
练习:
1.已知a、b为不共线的非零向量,且存在向量 c,使 c ∥ a, c ∥ b, 则
c =____
练习:判断正误
对于向量a , b
(1)若“│a│=│b│”,则“ a = b ” ( )
(2)若“a = b ”,则“│a│=│b│ ” ( )
在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等。
练习
1、若两个向量在同一直线上,则这两个向量是什么向量?
2、共线向量一定在一条直线上吗?
练习:
在质量、重力、速度、加速度、身高、面积、体积这些量中,哪些是数量?哪些是向量?
数量有:
向量有:
练习:
在质量、重力、速度、加速度、身高、面积、体积这些量中,哪些是数量?哪些是向量?
数量有:质量、身高、面积、体积
向量有:重力、速度、加速度
练习:
1、单位向量是否一定相等?
2、单位向量的大小是否一定相等?
练习:
1、单位向量是否一定相等?
2、单位向量的大小是否一定相等?
不一定
一定
练习:
1、平行向量是否一定方向相同?
2、不相等的向量一定不平行吗?
练习:
1、平行向量是否一定方向相同?
2、不相等的向量一定不平行吗?
不一定
不一定
当堂测试
1、下列物理量中, 不能称为向量的是 ( )
A.距离 B.加速度 C.力 D.位移
2、下列四个命题正确的是 ( )
A.两个单位向量一定相等 B.若与不共线,则与都是非零向量
C.共线的单位向量必相等 D.两个相等的向量起点、方向、长度必须都相同
3、下列说法错误的是 ( )
A.向量的长度与向量的长度相等 B.零向量与任意非零向量平行
C.长度相等方向相反的向量共线 D.方向相反的向量可能相等
4、对于以下命题:(1)平行向量一定相等; (2)不相等的向量一定不平行;
(3)共线向量一定相等;(4)相等向量一定共线。其中真命题的个数是 ( )
A.0个 B.1个 C.2个 D.3个
相等向量
零向量
单位向量
平行向量
共线向量
向量的方向
向量的大小
(长度,模)
有向线段
向 量
课时小结
