华师大版八年级数学下册 17.5 实践与探索课件(第1课时 共30张PPT)
文档属性
| 名称 | 华师大版八年级数学下册 17.5 实践与探索课件(第1课时 共30张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-11 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
17.5 实践与探索
课程讲授
新知导入
随堂练习
课堂小结
第17章 函数及其图象
第1课时 一次函数与二元一次方程组
知识要点
一次函数与二元一次方程之间的转化
学习目标
1.理解一次函数与二元一次方程(组)的关系;
2.会用图象法解决实际问题.
一次函数与二元一次方程组之间的联系
利用图象解决实际问题
一次函数与二元一次方程
一
y=kx+b(k≠0)
问题:看到一次函数,你能想到什么?
问题:看到二元一次方程,你又能想到什么?
x-y=5
它们有什么共同点?
y=x-5
一次函数与二元一次方程
一
x-y=5
问题:是不是所有的二元一次方程都可以转化为一次函数?
y=x-5
试一试:把下列二元一次方程化为一次函数.
(1)y-2x=1; (2)2y+x=4.
转化
解:(1)y=2x+1; (2)y=-0.5x+2.
下面我们来研究一次函数与二元一次方程的联系.
我们把方程3x+2y=6化成一次函数的形式:
…
-1.5
0
1.5
3
4.5
6
7.5
…
…
3
2
1
0
-1
-2
-3
…
x
对于这个函数,任意给出自变量x的一些值,可以求得相应的y值,列表如下:
表中每一对x、y的值代入方程3x+2y=6都成立,所以每组有序数对都是方程3x+2y=6的解.
以这些有序数对为坐标,在坐标平面内找出点作图,就得到二元一次方程3x+2y=6的图象.
由上可知,二元一次方程3x+2y=6的图象就是一次函数
的图象.它是一条直线,如图所示.
1
2
3
4
5
6
7
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
-5
8
3x+2y=6
y
归纳总结
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
二元一次方程组的图象解法
二
两个一次函数关系式可以写成
一个二元一次方程组
这两个一次函数的图象
问题?
相应的二元一次方程组的解
与
有什么关系呢?
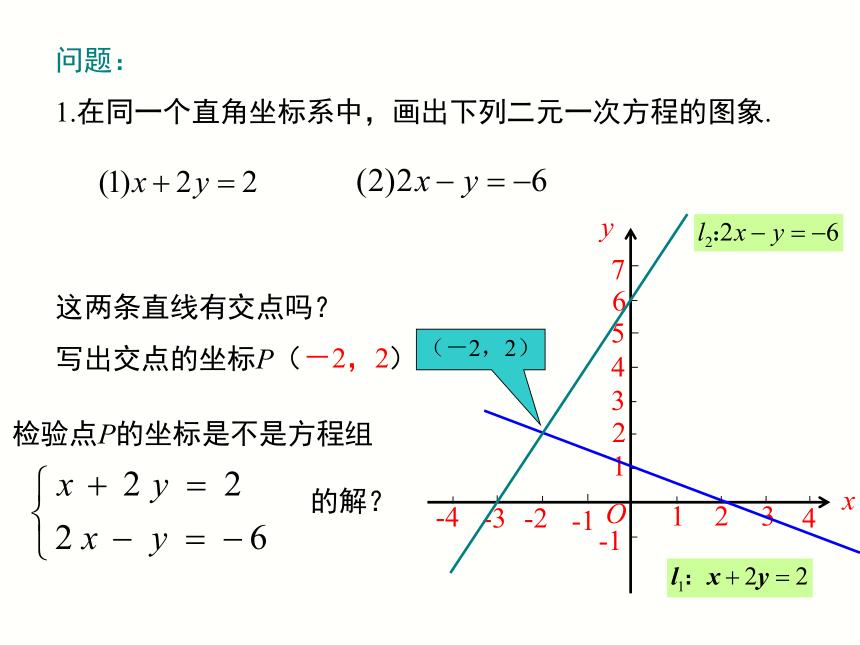
问题:
1.在同一个直角坐标系中,画出下列二元一次方程的图象.
这两条直线有交点吗?
写出交点的坐标P( )
检验点P的坐标是不是方程组
的解?
-2,2
(-2,2)
1
2
3
-1
-2
-3
-4
1
3
4
5
7
O
2
6
4
-1
x
y
通过上面的验证,我们发现这两条直线的交点坐标就是这个方程组的解,你能说出其中的道理吗?
直线l1
是方程x+2y=2
的图象,因此,直线l1
上的任意
一点的坐标都是方程l1
的解;
同理,直线l2
上的任意一点的
坐标都是方程2x-y=-6
的解. 所以直线
l1与l2
的交点P的
坐标就是方程x+2y=2
与2x-y=-6
的公共解.
也就是二元一次方程组
的解.
这样用作图的方法求解二元一次方程组的方法,叫做二元一次方程组的图象解法,由此我们发现数和形有着密不可分的联系.
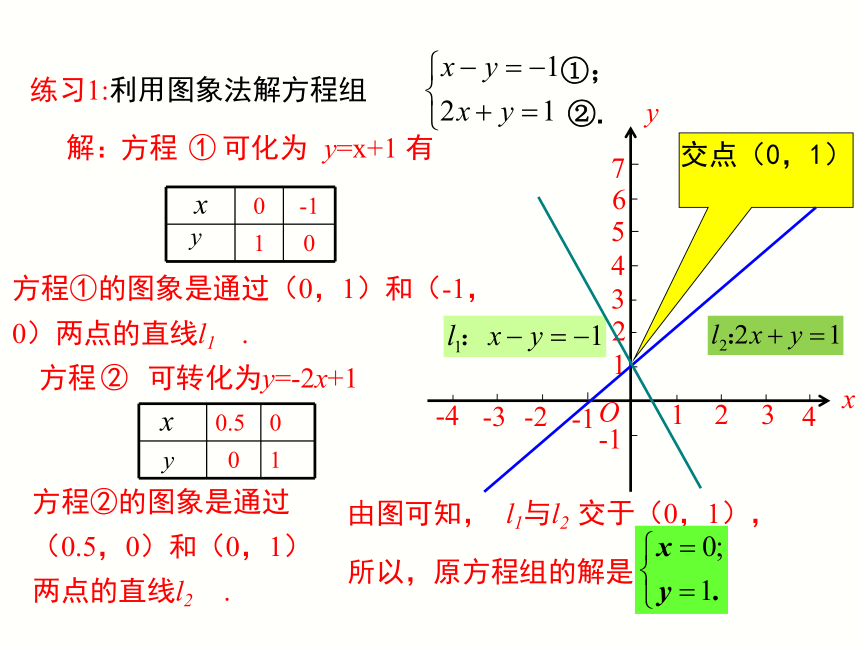
练习1:利用图象法解方程组
②.
①;
解:
0 -1
1 0
0.5 0
0 1
方程①的图象是通过(0,1)和(-1,0)两点的直线l1 .
方程②的图象是通过(0.5,0)和(0,1)两点的直线l2 .
由图可知,
l1与l2
交于(0,1),
所以,原方程组的解是
交点(0,1)
方程
①
可化为 y=x+1 有
方程
②
可转化为y=-2x+1
1
2
3
-1
-2
-3
-4
1
3
4
5
7
O
2
6
4
-1
x
y
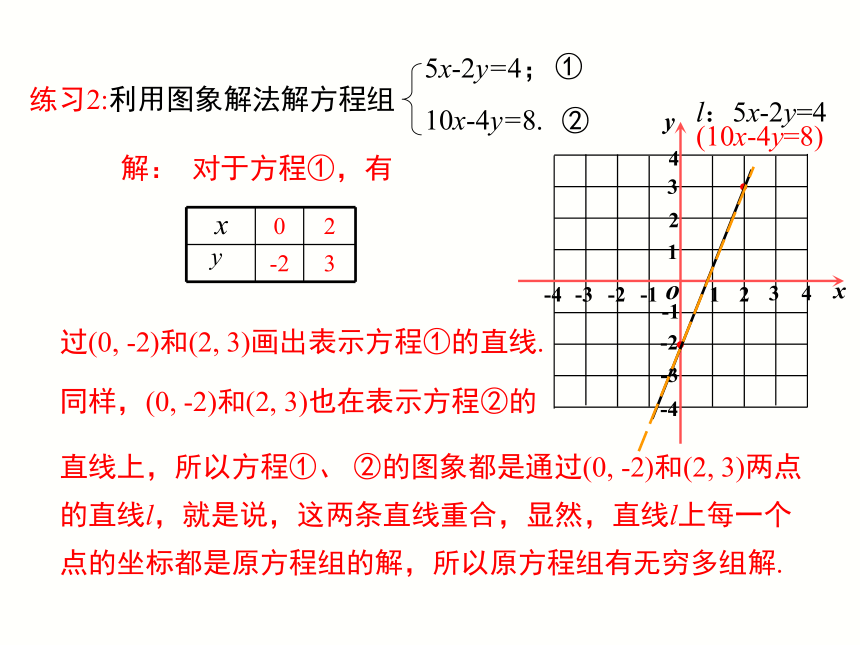
练习2:利用图象解法解方程组
5x-2y=4;
10x-4y=8.
解: 对于方程①,有
过(0, -2)和(2, 3)画出表示方程①的直线.
同样,(0, -2)和(2, 3)也在表示方程②的
直线上,所以方程①、 ②的图象都是通过(0, -2)和(2, 3)两点的直线l,就是说,这两条直线重合,显然,直线l上每一个点的坐标都是原方程组的解,所以原方程组有无穷多组解.
y
1
2
3
4
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
l:5x-2y=4
(10x-4y=8)
0 2
-2 3
①
②
练习3:利用图象法解方程组
3x+2y=-2,
6x+4y=4.
方程组的两个方程的图象有怎样的位置关系?方程组的情况怎样?
解:作出两个方程的图象,
1
2
3
4
5
6
7
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
-5
8
3x+2y = -2
6x+4y = 4
如图,两条直线平行,所以方程组无解.
y
一次函数
与方程组:
两直线y=
k1x+b1和
y=k2x+b2 两直线相交k1≠k2
两直线平行k1=k2,b1≠b2
两直线重合k1=k2,b1=b2
归纳总结
归纳总结
通过以上探讨我们知道,用图象法解二元一次方程组时,应先在同一平面直角坐标系内画出这两个二元一次方程的图象,这两条直线若相交,其交点的坐标就是方程组的解.
利用图象法解二元一次方程组的一般步骤
①两个方程分别转化为一次函数
②在同一坐标系中画出两个函数图象
③找出图象交点坐标
④写出方程组的解
例: 学校有一批复印任务,
甲复印社:按每100页40元计费.
乙复印社:学校先按月付给一定数额的承包费,
则按每100页15元收费.
两复印社每月收费情况
利用图象解决实际问题
三
1、乙复印社的每月承包费是多少?
2、 当每月复印多少页时,
两复印社实际收费相同?
收多少元?
4、根据图象可看出方程组
的 解吗?
5、 从图象中可知当x_________时, y >y 的?
从图象中可知当x_________时, y <y 的?
6、如果每月复印页数在1 200页左右,那么应选择哪
个复印社? 800页呢?500页呢?
甲
甲
乙
乙
·
> 800
< 800
y= 0.4x
y= 0.15x+200
y= 0.4x
y= 0.15x+200
3.求两函数关系式
y= 0.4x
y= 0.15x+200
随堂练习
随堂练习
随堂练习
1
2
随堂练习
4、
1、
随堂练习
知识点二:利用函数的图象和性质解决实际问题
2.已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的函数表达式;
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
随堂练习
3.
随堂练习
4.某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数.已知行李质量为20 kg时需付行李费2元,行李质量为50 kg时需付行李费8元.
(1)当行李的质量x超过规定时,求y与x之间的函数表达式;
随堂练习
(2)求旅客最多可免费携带行李的质量.
随堂练习
5、
课堂小结
1、二元一次方程与一次函数的关系
(1)以一个二元一次方程的任意一个解为坐标的点,它一定在这个一次函数的图象上;
(2)一个一次函数图象上的任意一个点,它的坐标一定能适合某一个方程.
课堂小结
2、二元一次方程组的解与一次函数图象交点的关系
(1)一般地,以一个二元一次方程组的解为坐标的点,可以看作两个一次函数所组成的图象的交点(即是两条直线的交点).
(2)两个一次函数的所组成的图象的交点(即两条直线的交点),可以看成是某个二元一次方程组的解.
谢谢大家!
作业:
1、课本61页1、2题;
2、课本64页1、2、3、4题。
17.5 实践与探索
课程讲授
新知导入
随堂练习
课堂小结
第17章 函数及其图象
第1课时 一次函数与二元一次方程组
知识要点
一次函数与二元一次方程之间的转化
学习目标
1.理解一次函数与二元一次方程(组)的关系;
2.会用图象法解决实际问题.
一次函数与二元一次方程组之间的联系
利用图象解决实际问题
一次函数与二元一次方程
一
y=kx+b(k≠0)
问题:看到一次函数,你能想到什么?
问题:看到二元一次方程,你又能想到什么?
x-y=5
它们有什么共同点?
y=x-5
一次函数与二元一次方程
一
x-y=5
问题:是不是所有的二元一次方程都可以转化为一次函数?
y=x-5
试一试:把下列二元一次方程化为一次函数.
(1)y-2x=1; (2)2y+x=4.
转化
解:(1)y=2x+1; (2)y=-0.5x+2.
下面我们来研究一次函数与二元一次方程的联系.
我们把方程3x+2y=6化成一次函数的形式:
…
-1.5
0
1.5
3
4.5
6
7.5
…
…
3
2
1
0
-1
-2
-3
…
x
对于这个函数,任意给出自变量x的一些值,可以求得相应的y值,列表如下:
表中每一对x、y的值代入方程3x+2y=6都成立,所以每组有序数对都是方程3x+2y=6的解.
以这些有序数对为坐标,在坐标平面内找出点作图,就得到二元一次方程3x+2y=6的图象.
由上可知,二元一次方程3x+2y=6的图象就是一次函数
的图象.它是一条直线,如图所示.
1
2
3
4
5
6
7
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
-5
8
3x+2y=6
y
归纳总结
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
二元一次方程组的图象解法
二
两个一次函数关系式可以写成
一个二元一次方程组
这两个一次函数的图象
问题?
相应的二元一次方程组的解
与
有什么关系呢?
问题:
1.在同一个直角坐标系中,画出下列二元一次方程的图象.
这两条直线有交点吗?
写出交点的坐标P( )
检验点P的坐标是不是方程组
的解?
-2,2
(-2,2)
1
2
3
-1
-2
-3
-4
1
3
4
5
7
O
2
6
4
-1
x
y
通过上面的验证,我们发现这两条直线的交点坐标就是这个方程组的解,你能说出其中的道理吗?
直线l1
是方程x+2y=2
的图象,因此,直线l1
上的任意
一点的坐标都是方程l1
的解;
同理,直线l2
上的任意一点的
坐标都是方程2x-y=-6
的解. 所以直线
l1与l2
的交点P的
坐标就是方程x+2y=2
与2x-y=-6
的公共解.
也就是二元一次方程组
的解.
这样用作图的方法求解二元一次方程组的方法,叫做二元一次方程组的图象解法,由此我们发现数和形有着密不可分的联系.
练习1:利用图象法解方程组
②.
①;
解:
0 -1
1 0
0.5 0
0 1
方程①的图象是通过(0,1)和(-1,0)两点的直线l1 .
方程②的图象是通过(0.5,0)和(0,1)两点的直线l2 .
由图可知,
l1与l2
交于(0,1),
所以,原方程组的解是
交点(0,1)
方程
①
可化为 y=x+1 有
方程
②
可转化为y=-2x+1
1
2
3
-1
-2
-3
-4
1
3
4
5
7
O
2
6
4
-1
x
y
练习2:利用图象解法解方程组
5x-2y=4;
10x-4y=8.
解: 对于方程①,有
过(0, -2)和(2, 3)画出表示方程①的直线.
同样,(0, -2)和(2, 3)也在表示方程②的
直线上,所以方程①、 ②的图象都是通过(0, -2)和(2, 3)两点的直线l,就是说,这两条直线重合,显然,直线l上每一个点的坐标都是原方程组的解,所以原方程组有无穷多组解.
y
1
2
3
4
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
l:5x-2y=4
(10x-4y=8)
0 2
-2 3
①
②
练习3:利用图象法解方程组
3x+2y=-2,
6x+4y=4.
方程组的两个方程的图象有怎样的位置关系?方程组的情况怎样?
解:作出两个方程的图象,
1
2
3
4
5
6
7
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
-5
8
3x+2y = -2
6x+4y = 4
如图,两条直线平行,所以方程组无解.
y
一次函数
与方程组:
两直线y=
k1x+b1和
y=k2x+b2 两直线相交k1≠k2
两直线平行k1=k2,b1≠b2
两直线重合k1=k2,b1=b2
归纳总结
归纳总结
通过以上探讨我们知道,用图象法解二元一次方程组时,应先在同一平面直角坐标系内画出这两个二元一次方程的图象,这两条直线若相交,其交点的坐标就是方程组的解.
利用图象法解二元一次方程组的一般步骤
①两个方程分别转化为一次函数
②在同一坐标系中画出两个函数图象
③找出图象交点坐标
④写出方程组的解
例: 学校有一批复印任务,
甲复印社:按每100页40元计费.
乙复印社:学校先按月付给一定数额的承包费,
则按每100页15元收费.
两复印社每月收费情况
利用图象解决实际问题
三
1、乙复印社的每月承包费是多少?
2、 当每月复印多少页时,
两复印社实际收费相同?
收多少元?
4、根据图象可看出方程组
的 解吗?
5、 从图象中可知当x_________时, y >y 的?
从图象中可知当x_________时, y <y 的?
6、如果每月复印页数在1 200页左右,那么应选择哪
个复印社? 800页呢?500页呢?
甲
甲
乙
乙
·
> 800
< 800
y= 0.4x
y= 0.15x+200
y= 0.4x
y= 0.15x+200
3.求两函数关系式
y= 0.4x
y= 0.15x+200
随堂练习
随堂练习
随堂练习
1
2
随堂练习
4、
1、
随堂练习
知识点二:利用函数的图象和性质解决实际问题
2.已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的函数表达式;
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
随堂练习
3.
随堂练习
4.某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数.已知行李质量为20 kg时需付行李费2元,行李质量为50 kg时需付行李费8元.
(1)当行李的质量x超过规定时,求y与x之间的函数表达式;
随堂练习
(2)求旅客最多可免费携带行李的质量.
随堂练习
5、
课堂小结
1、二元一次方程与一次函数的关系
(1)以一个二元一次方程的任意一个解为坐标的点,它一定在这个一次函数的图象上;
(2)一个一次函数图象上的任意一个点,它的坐标一定能适合某一个方程.
课堂小结
2、二元一次方程组的解与一次函数图象交点的关系
(1)一般地,以一个二元一次方程组的解为坐标的点,可以看作两个一次函数所组成的图象的交点(即是两条直线的交点).
(2)两个一次函数的所组成的图象的交点(即两条直线的交点),可以看成是某个二元一次方程组的解.
谢谢大家!
作业:
1、课本61页1、2题;
2、课本64页1、2、3、4题。
