2.3.2 平行线的性质课件(共16张PPT)
文档属性
| 名称 | 2.3.2 平行线的性质课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
数学北师大版
七年级
3 平行线的性质第2课时
例1根据图2--20回答下列问题:
(1)若∠1=∠2,则可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,则可以判定哪两条直线平行?根据是什么?
(3)若∠2+∠3= 180°,则可以判定哪两条直线平行?根据是什么?
解: (1)∠1与∠2是内错角,若∠1=∠2,则根据“内错角相等,两直线平行”,可得BF// CE;
(2)∠2与∠M是同位角,若∠2=∠M,则根据“同位角相等,两直线平行”,可得AM// BF;
(3)∠2与∠3是同旁内角,若∠2+∠3= 180°,则根据“同旁内角互补,两直线平行”,可得AC// MD.
练习1.如图,AE∥CD,若∠1 = 37°,∠D =54°,求∠2 和∠BAE的度数.
解:∵AE∥CD,∠1 = 37° (已知)
∴ ∠2 = ∠1 =37°
(两直线平行,内错角相等)
∵ AE∥CD,∠D =54 °(已知)
∴ ∠BAE = ∠D =54°
(两直线平行,同位角相等) )
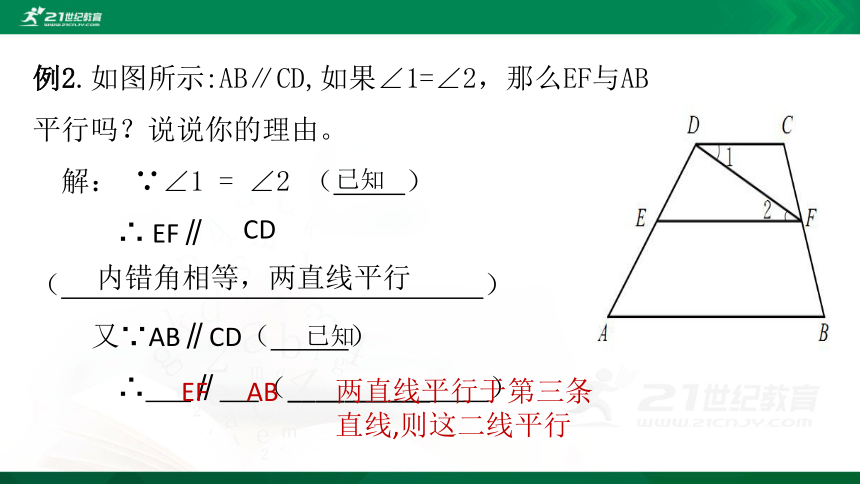
例2.如图所示:AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由。
解: ∵∠1 = ∠2 ( )
∴ EF∥ ( )
又∵AB∥CD( )
∴ ∥ (__________ )
已知
CD
AB
EF
已知
内错角相等,两直线平行
两直线平行于第三条直线,则这二线平行
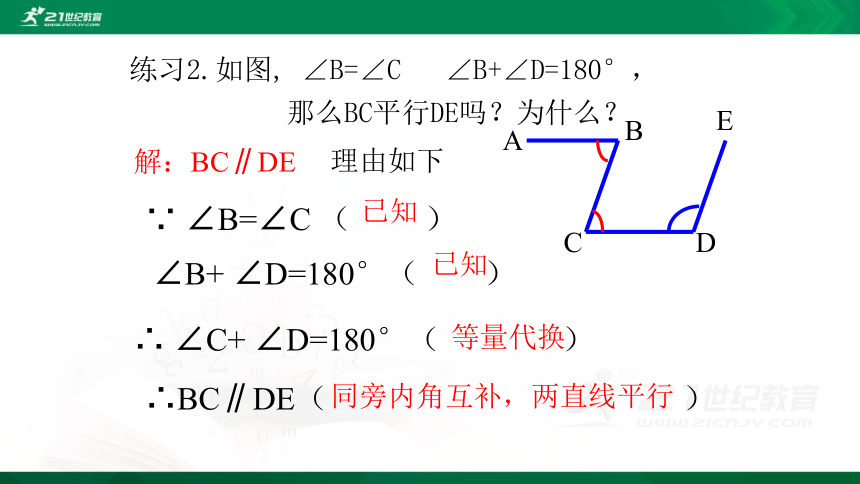
练习2.如图, ∠B=∠C ∠B+∠D=180°,
那么BC平行DE吗?为什么?
A
B
C
D
E
解:BC∥DE
理由如下
∵ ∠B=∠C ( )
已知
∠B+ ∠D=180°( )
已知
∴ ∠C+ ∠D=180°( )
等量代换
∴BC∥DE( )
同旁内角互补,两直线平行
例3: 如图,已知直线 a∥b,
直线 c∥d, ∠1 = 107°,
求 ∠2, ∠3 的度数.
解:∵a//b(已知)?
∴∠2 = ∠1=107°
(两直线平行,内错角相等)
∵c//d(已知)
∴∠1 +∠3=180°
(两直线平行,同旁内角互补 )
∴∠3= 180°﹣ ∠1 =73°
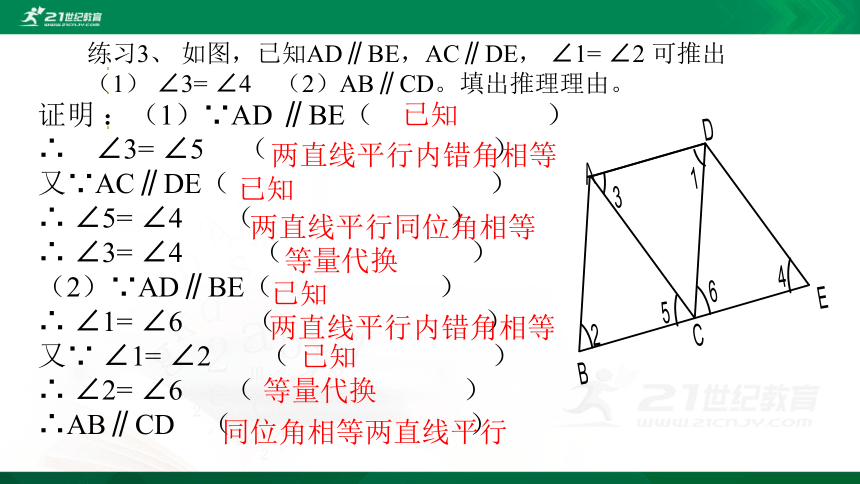
证明 :(1)∵AD ∥BE( )
∴ ∠3= ∠5 ( )
又∵AC∥DE( )
∴ ∠5= ∠4 ( )
∴ ∠3= ∠4 ( )
(2)∵AD∥BE( )
∴ ∠1= ∠6 ( )
又∵ ∠1= ∠2 ( )
∴ ∠2= ∠6 ( )
∴AB∥CD ( )
#k#b#1#新#课#
已知
两直线平行内错角相等
已知
两直线平行同位角相等
等量代换
已知
两直线平行内错角相等
同位角相等两直线平行
等量代换
已知
练习3、 如图,已知AD∥BE,AC∥DE, ∠1= ∠2 可推出
(1) ∠3= ∠4 (2)AB∥CD。填出推理理由。
1.如图,AB∥CD,直线EF分别交AB,CD于点E,F,点G是AB上一点,GO⊥EF于点O,∠1=60°,求∠2的度数.
提高训练
解析:∵OG⊥EF,(已知)
∠EOG=90°,(垂直的定义)
∴∠2+∠GEO=90°.(三角形内角和定理)
又∵AB∥CD,(已知)
∴∠GEF=∠1=60°.(两直线平行,内错角相等)∴∠2=30°.(等式的性质)
分析:先根据垂直的定义得出∠EOG=90°,再由三角形内角和定理得出∠2+∠GEO=90°,
2.如图,AD平分∠BAC,DE∥AC,DF∥AB,图中∠1与∠2有什么关系?为什么?
答案:∠1=∠2.
解析:∠1=∠2.理由如下:
DE∥AC,DF∥AB,∴∠1=∠DAF,∠2=∠DAE,
又∵AD平分∠BAC,
∴∠DAF=∠DAE,∴∠1=∠2.
【分析】根据两直线平行内错角相等,及角平分线的性质,可得粗结论.
3.解放战争时期,某天江南某游击队从村庄A处出发向正东方向行进,此时有一支残匪在游击队的东北方向B处,残匪沿北偏东60°方向向C村进发,游击队步行到A′(A′在B的正南方向)处时,突然接到上级命令,决定改变行进方向,沿北偏东30°方向赶往C村,问:游击队的进发方向A′C与残匪的行进方向BC至少成多大角度时,才能保证C村村民不受伤害?
解析:如图.∵BA′∥CM,∴∠A′CM=∠BA′C=30°.
∵CN∥BE,∴∠BCN=∠CBE=30°,
∴∠BCA′=90°-30°-30°=30°,故A′C与BC的夹角至少为30°时,才能保证C村村民不受伤害.
【分析】先根据题意作出辅助线,构造出平行线,再根据平行线的性质解答即可.
4.如图,AB∥CD,AD∥BC,若∠A=73°,求∠B、∠C、∠D的度数.
答案:∠C73°,∠B=∠D=107°.
解析:【解答】∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,
∴∠C=∠A=73°,∴∠B=∠D=180°-∠A=107°.
【分析】由AB∥CD,AD∥BC,可得四边形ABCD是平行四边形,根据平行四边形的性质,即可求得答案.
5.如图,已知在△ABC中,AD平分∠EAC且AD∥BC,那么∠B=∠C吗?请说明理由.
解析:【解答】∠B=∠C.
理由如下∵AD∥BC∴∠EAD=∠B,
∠DAC=∠C.∵AD平分∠EAC,
∴∠EAD=∠DAC.∴∠B=∠C.
【分析】先根据平行线性质得到∠EAD=∠B,∠DAC=∠C,再根据角平分线的性质得到∠EAD=∠DAC,从而推出∠B=∠C.
1.必做题: 课本54页 习题2.6
1、2、3、4、 6
2.选做题:
如图EF∥AD,∠1=∠2,
∠BAC=70 °,求∠AGD的度数。
布置作业
1.如图,BD平分∠_ABC,点E在BC上,EF// AB.若∠CEF=100°,则∠ABD的度数为( )
B
A.60°
B.50°
C.40°
D.30
2.(2018. 自贡中考)如图,若∠1=55°,则∠2的度数是( )
A.50°
B.45°
C.40°
D.35°
课外作业
D
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
七年级
3 平行线的性质第2课时
例1根据图2--20回答下列问题:
(1)若∠1=∠2,则可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,则可以判定哪两条直线平行?根据是什么?
(3)若∠2+∠3= 180°,则可以判定哪两条直线平行?根据是什么?
解: (1)∠1与∠2是内错角,若∠1=∠2,则根据“内错角相等,两直线平行”,可得BF// CE;
(2)∠2与∠M是同位角,若∠2=∠M,则根据“同位角相等,两直线平行”,可得AM// BF;
(3)∠2与∠3是同旁内角,若∠2+∠3= 180°,则根据“同旁内角互补,两直线平行”,可得AC// MD.
练习1.如图,AE∥CD,若∠1 = 37°,∠D =54°,求∠2 和∠BAE的度数.
解:∵AE∥CD,∠1 = 37° (已知)
∴ ∠2 = ∠1 =37°
(两直线平行,内错角相等)
∵ AE∥CD,∠D =54 °(已知)
∴ ∠BAE = ∠D =54°
(两直线平行,同位角相等) )
例2.如图所示:AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由。
解: ∵∠1 = ∠2 ( )
∴ EF∥ ( )
又∵AB∥CD( )
∴ ∥ (__________ )
已知
CD
AB
EF
已知
内错角相等,两直线平行
两直线平行于第三条直线,则这二线平行
练习2.如图, ∠B=∠C ∠B+∠D=180°,
那么BC平行DE吗?为什么?
A
B
C
D
E
解:BC∥DE
理由如下
∵ ∠B=∠C ( )
已知
∠B+ ∠D=180°( )
已知
∴ ∠C+ ∠D=180°( )
等量代换
∴BC∥DE( )
同旁内角互补,两直线平行
例3: 如图,已知直线 a∥b,
直线 c∥d, ∠1 = 107°,
求 ∠2, ∠3 的度数.
解:∵a//b(已知)?
∴∠2 = ∠1=107°
(两直线平行,内错角相等)
∵c//d(已知)
∴∠1 +∠3=180°
(两直线平行,同旁内角互补 )
∴∠3= 180°﹣ ∠1 =73°
证明 :(1)∵AD ∥BE( )
∴ ∠3= ∠5 ( )
又∵AC∥DE( )
∴ ∠5= ∠4 ( )
∴ ∠3= ∠4 ( )
(2)∵AD∥BE( )
∴ ∠1= ∠6 ( )
又∵ ∠1= ∠2 ( )
∴ ∠2= ∠6 ( )
∴AB∥CD ( )
#k#b#1#新#课#
已知
两直线平行内错角相等
已知
两直线平行同位角相等
等量代换
已知
两直线平行内错角相等
同位角相等两直线平行
等量代换
已知
练习3、 如图,已知AD∥BE,AC∥DE, ∠1= ∠2 可推出
(1) ∠3= ∠4 (2)AB∥CD。填出推理理由。
1.如图,AB∥CD,直线EF分别交AB,CD于点E,F,点G是AB上一点,GO⊥EF于点O,∠1=60°,求∠2的度数.
提高训练
解析:∵OG⊥EF,(已知)
∠EOG=90°,(垂直的定义)
∴∠2+∠GEO=90°.(三角形内角和定理)
又∵AB∥CD,(已知)
∴∠GEF=∠1=60°.(两直线平行,内错角相等)∴∠2=30°.(等式的性质)
分析:先根据垂直的定义得出∠EOG=90°,再由三角形内角和定理得出∠2+∠GEO=90°,
2.如图,AD平分∠BAC,DE∥AC,DF∥AB,图中∠1与∠2有什么关系?为什么?
答案:∠1=∠2.
解析:∠1=∠2.理由如下:
DE∥AC,DF∥AB,∴∠1=∠DAF,∠2=∠DAE,
又∵AD平分∠BAC,
∴∠DAF=∠DAE,∴∠1=∠2.
【分析】根据两直线平行内错角相等,及角平分线的性质,可得粗结论.
3.解放战争时期,某天江南某游击队从村庄A处出发向正东方向行进,此时有一支残匪在游击队的东北方向B处,残匪沿北偏东60°方向向C村进发,游击队步行到A′(A′在B的正南方向)处时,突然接到上级命令,决定改变行进方向,沿北偏东30°方向赶往C村,问:游击队的进发方向A′C与残匪的行进方向BC至少成多大角度时,才能保证C村村民不受伤害?
解析:如图.∵BA′∥CM,∴∠A′CM=∠BA′C=30°.
∵CN∥BE,∴∠BCN=∠CBE=30°,
∴∠BCA′=90°-30°-30°=30°,故A′C与BC的夹角至少为30°时,才能保证C村村民不受伤害.
【分析】先根据题意作出辅助线,构造出平行线,再根据平行线的性质解答即可.
4.如图,AB∥CD,AD∥BC,若∠A=73°,求∠B、∠C、∠D的度数.
答案:∠C73°,∠B=∠D=107°.
解析:【解答】∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,
∴∠C=∠A=73°,∴∠B=∠D=180°-∠A=107°.
【分析】由AB∥CD,AD∥BC,可得四边形ABCD是平行四边形,根据平行四边形的性质,即可求得答案.
5.如图,已知在△ABC中,AD平分∠EAC且AD∥BC,那么∠B=∠C吗?请说明理由.
解析:【解答】∠B=∠C.
理由如下∵AD∥BC∴∠EAD=∠B,
∠DAC=∠C.∵AD平分∠EAC,
∴∠EAD=∠DAC.∴∠B=∠C.
【分析】先根据平行线性质得到∠EAD=∠B,∠DAC=∠C,再根据角平分线的性质得到∠EAD=∠DAC,从而推出∠B=∠C.
1.必做题: 课本54页 习题2.6
1、2、3、4、 6
2.选做题:
如图EF∥AD,∠1=∠2,
∠BAC=70 °,求∠AGD的度数。
布置作业
1.如图,BD平分∠_ABC,点E在BC上,EF// AB.若∠CEF=100°,则∠ABD的度数为( )
B
A.60°
B.50°
C.40°
D.30
2.(2018. 自贡中考)如图,若∠1=55°,则∠2的度数是( )
A.50°
B.45°
C.40°
D.35°
课外作业
D
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
