2020春北师大版七年级数学下册 4.1认识三角形教学课件(共20张ppt)
文档属性
| 名称 | 2020春北师大版七年级数学下册 4.1认识三角形教学课件(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 846.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 17:31:29 | ||
图片预览








文档简介
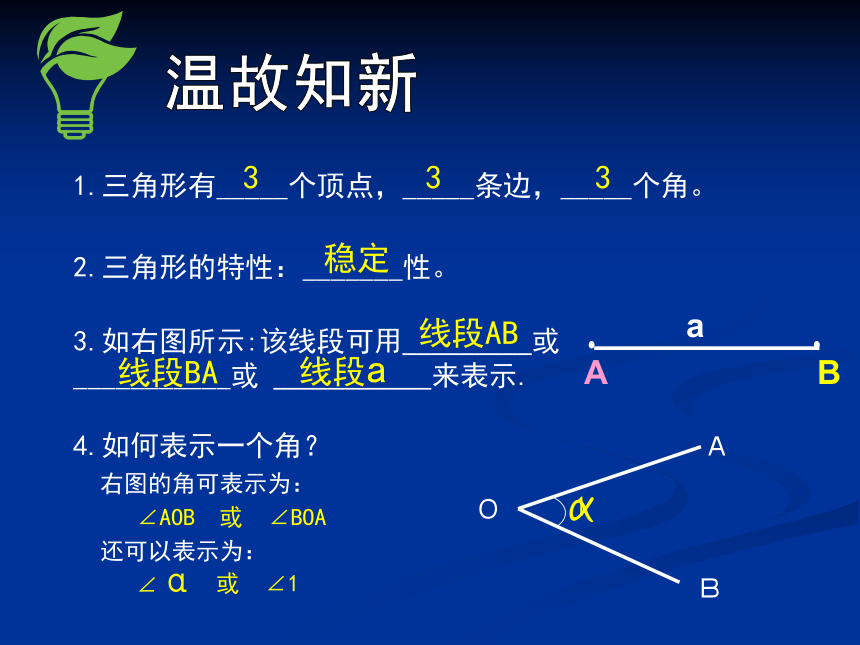
课件20张PPT。认识三角形(第1课时)温故知新1.三角形有_____个顶点,_____条边,_____个角。2.三角形的特性:_______性。3.如右图所示:该线段可用_________或
___________或 ___________来表示. 4.如何表示一个角?右图的角可表示为:∠AOB 或 ∠BOA∠αAOBα1333稳定线段AB线段BA线段a或 ∠1还可以表示为:温故知新两点之间,线段最短学以致用——三角形的定义问题思考:任意的三条边都能组成三角形吗?尝试用自己的语言来描述你心目中的三角形。1.三角形的定义: 由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。定义三要素:1.不在同一直线上2.三条线段3.首尾顺次相接AB顶点:边:2.三角形表示方法:点A点B点C我们把顶点是A,B,C的三角形 记作 :△ABC,读作:三角形ABCC边AB或BA边BC或CB边AC或CA内角:? A
或? BAC
或? CAB?B
或? ABC
或? CBA?C
或?BCA
或?ACB 注:和顶点相对的边可以用该顶点所对应的小写字母来表示,我们把边BC(或a)叫做点A的对边,把边AB(或c)、AC(或b) 分别叫做点A的邻边.acb学以致用——三角形的性质 是否任意三条线段都能构成三角形呢?这三边要符合哪些条件呢?小组实验:
每小组都有一个三角形,要求把三角形三边剪开,比较一下任意两边之和于第三边长度关系?小组分工,并做好记录。abcabcb + c根据实验数据显示aa + cba + bc>>>得出结论:三角形任意两边之和大于第三边。把三边剪开得568131114ABCDE随堂练习(一)2.如右图,图中有哪几个三角形?3.如右图,包含∠ADC的三角形有哪些?解:图中三角形有△ABC△ABE△ADC△ABD△ADE△AEC△ADE△ADC解:图中包含∠ADC的三角形有4.如右图,∠B的对边有哪些?解:∠B的对边有边AD,边AE,边AC1.小强用三根木棒组成的图形,其中符合三角形概念是( )BACC随堂练习(二) 1. 下列每组数分别是三根小木棒的长度,用它 们可以摆成一个三角形吗?并说明你的理由。①3cm, 4cm, 5cm② 8cm, 7cm, 15cm③13cm, 12cm, 20cm④ 5cm, 5cm, 11cm(√) (√) (× )(× )2.如果三条线段 a , b , c能组成三角形,那么它们的长度可能是 ( )A 1 : 2 : 4 C 3 : 4 : 7 B 1 : 3 : 4 D 2 : 3: 4 D3. 元宵节的晚上,房梁上亮起了彩灯,装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢?说明你的理由。ABC你知道吗 为什么经常有行人斜穿马路而不走人行横道
人行横道用所学的数学知识解释,“他”为何要这么做?2.两点之间的所有连线中,线段最短1.三角形任意两边之和大于第三边4.学以致用——三角形的性质 刚才小组间通过动手操作,数据证明了三角行任意两边之和大与第三边,那么,任意两边之差和第三边又是怎样的关系呢?试着把刚才你们小组的数据做个计算,并填表
你发现了:三角形任意两边之差小与第三边a︱b - c︱b︱a-c︱c︱a -b︱ab - c﹤ba -c﹤ca-b﹤568231随堂练习(三) 有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?解题技巧:
三角形第三边的取值范围是:两边之差<第三边<两边之和1.三角形的概念
2.三角形的三要素
3.三角形的表示方法
4.三角形三边之间的关系本节课的学习你有哪些收获?课堂小结祝:
学业有成!
再见!
___________或 ___________来表示. 4.如何表示一个角?右图的角可表示为:∠AOB 或 ∠BOA∠αAOBα1333稳定线段AB线段BA线段a或 ∠1还可以表示为:温故知新两点之间,线段最短学以致用——三角形的定义问题思考:任意的三条边都能组成三角形吗?尝试用自己的语言来描述你心目中的三角形。1.三角形的定义: 由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。定义三要素:1.不在同一直线上2.三条线段3.首尾顺次相接AB顶点:边:2.三角形表示方法:点A点B点C我们把顶点是A,B,C的三角形 记作 :△ABC,读作:三角形ABCC边AB或BA边BC或CB边AC或CA内角:? A
或? BAC
或? CAB?B
或? ABC
或? CBA?C
或?BCA
或?ACB 注:和顶点相对的边可以用该顶点所对应的小写字母来表示,我们把边BC(或a)叫做点A的对边,把边AB(或c)、AC(或b) 分别叫做点A的邻边.acb学以致用——三角形的性质 是否任意三条线段都能构成三角形呢?这三边要符合哪些条件呢?小组实验:
每小组都有一个三角形,要求把三角形三边剪开,比较一下任意两边之和于第三边长度关系?小组分工,并做好记录。abcabcb + c根据实验数据显示aa + cba + bc>>>得出结论:三角形任意两边之和大于第三边。把三边剪开得568131114ABCDE随堂练习(一)2.如右图,图中有哪几个三角形?3.如右图,包含∠ADC的三角形有哪些?解:图中三角形有△ABC△ABE△ADC△ABD△ADE△AEC△ADE△ADC解:图中包含∠ADC的三角形有4.如右图,∠B的对边有哪些?解:∠B的对边有边AD,边AE,边AC1.小强用三根木棒组成的图形,其中符合三角形概念是( )BACC随堂练习(二) 1. 下列每组数分别是三根小木棒的长度,用它 们可以摆成一个三角形吗?并说明你的理由。①3cm, 4cm, 5cm② 8cm, 7cm, 15cm③13cm, 12cm, 20cm④ 5cm, 5cm, 11cm(√) (√) (× )(× )2.如果三条线段 a , b , c能组成三角形,那么它们的长度可能是 ( )A 1 : 2 : 4 C 3 : 4 : 7 B 1 : 3 : 4 D 2 : 3: 4 D3. 元宵节的晚上,房梁上亮起了彩灯,装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢?说明你的理由。ABC你知道吗 为什么经常有行人斜穿马路而不走人行横道
人行横道用所学的数学知识解释,“他”为何要这么做?2.两点之间的所有连线中,线段最短1.三角形任意两边之和大于第三边4.学以致用——三角形的性质 刚才小组间通过动手操作,数据证明了三角行任意两边之和大与第三边,那么,任意两边之差和第三边又是怎样的关系呢?试着把刚才你们小组的数据做个计算,并填表
你发现了:三角形任意两边之差小与第三边a︱b - c︱b︱a-c︱c︱a -b︱ab - c﹤ba -c﹤ca-b﹤568231随堂练习(三) 有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?解题技巧:
三角形第三边的取值范围是:两边之差<第三边<两边之和1.三角形的概念
2.三角形的三要素
3.三角形的表示方法
4.三角形三边之间的关系本节课的学习你有哪些收获?课堂小结祝:
学业有成!
再见!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
