26.2 实际问题与反比例函数同步测试题(含解析)
文档属性
| 名称 | 26.2 实际问题与反比例函数同步测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 18:32:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2019-2020学年九年级下学期
26.2实际问题与反比例函数
(时间60分钟 总分100分)
一、选择题(每小题5分,共30分)
1.下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
Ax与y都是变量,且x是自变量,y是函数
B.用电量每增加1千瓦时,电费增加0.55元
C.若用电量为8千瓦时,则应交电费4.4元
D.y是x的反比例函数
2.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷
3.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也随之改变,密度/(单位:kg/m)是体积V(单位:m)的反比例函数,它的图象如图所示,当V= 10m时,气体的密度是( )
A. B. C. D.
4.当压力F(N)一定时,物体所受的压强p(Pa)与受力面积S(m)的函数关系式
(),这个函数的图象大致是( )
A. B. C. D.
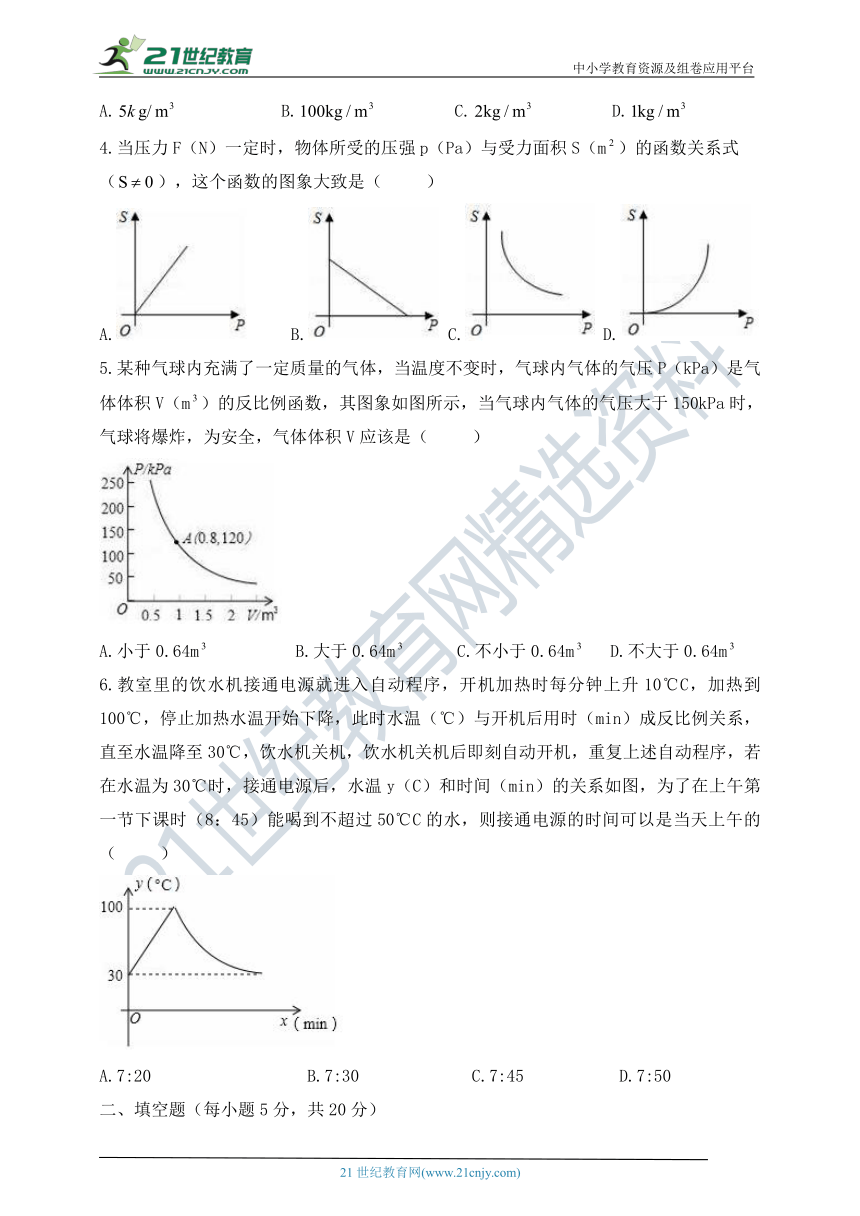
5.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m)的反比例函数,其图象如图所示,当气球内气体的气压大于150kPa时,气球将爆炸,为安全,气体体积V应该是( )
A.小于0.64m B.大于0.64m C.不小于0.64m D.不大于0.64m
6.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃C,加热到100℃,停止加热水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序,若在水温为30℃时,接通电源后,水温y(C)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃C的水,则接通电源的时间可以是当天上午的( )
A.7:20 B.7:30 C.7:45 D.7:50
二、填空题(每小题5分,共20分)
7.每年春季为预防流感,某校利用休息日对教室进行药熏消毒,已知药物燃烧过程及燃烧完后空气中白含药量y(mg/m)与时间(h)之间的关系如图所示,根据消毒要求,空气中的含药量不低于3mg/m且持续时间不能低于10h.请你帮助计算一下,当空气中的含药量不低于3mg/m时,持续时间可以达到______h
8.近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,贝眼镜度数y与镜片焦距x之间的函数关系式为_______.(无需确定x的取值范围)
9.如图所示,在某一电路中,保持电压不变,电阻R(欧)与电流(安)之间的函数关系式是______这一电路的电压为______伏
10.若梯形的下底长为x,上底长为下底长的3,高为y,面积为60,则y与x的函数解析式是_______(不考虑x的取值范围).
三、解答题(共5题,共50分)
11.知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与铝用量有如下关系:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当易拉罐底面半径为2.4cm时,易拉罐需要的用铝量是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少时比较适宜?说说你的理由
(4)粗略说一说易拉,底面半径对所需铝质量的影响.
12.如图,一辆汽车从甲地到乙地的行驶时间(h)与行驶速度v(km/h)的函数关系如图所示,根据图象提的信息,求:
(1)t与v之间的函数关系式
(2)若要在3h内到达乙地,则汽车的速度应不低于多少?
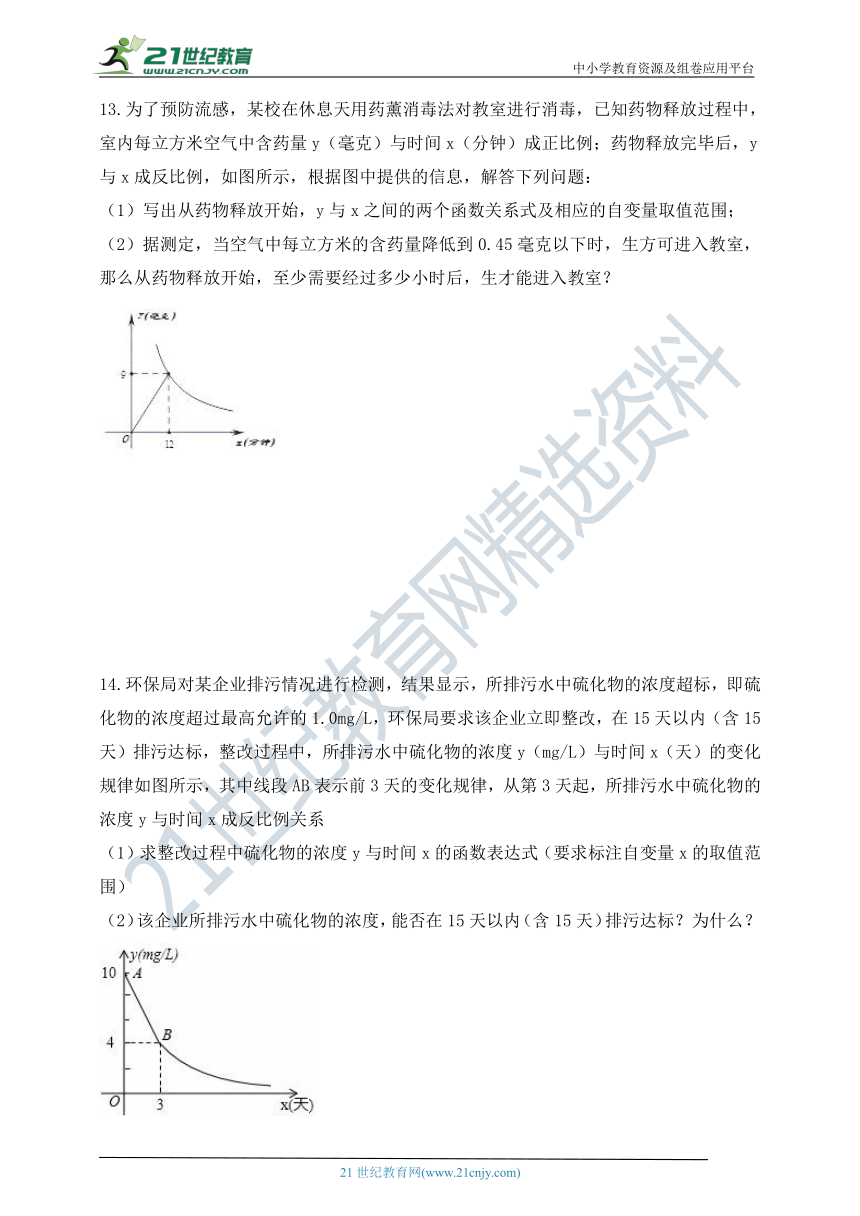
13.为了预防流感,某校在休息天用药薰消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示,根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,生才能进入教室?
14.环保局对某企业排污情况进行检测,结果显示,所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L,环保局要求该企业立即整改,在15天以内(含15天)排污达标,整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系
(1)求整改过程中硫化物的浓度y与时间x的函数表达式(要求标注自变量x的取值范围)
(2)该企业所排污水中硫化物的浓度,能否在15天以内(含15天)排污达标?为什么?
15.保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2017年1月的利润为200万元,设2017年1月为第1个月,第x个月的利润为y万元,由于排污超标,该厂决定从2017年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例,到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图)
(1)分别求该化工厂治污期间及治污改造工程完工后,y与x之间的函数关系式;
(2)治污改造工程顺利完工后经过几个月,该厂月利润才能达到200万元?
(3)当月利润少于100万元时,为该厂资金紧张期,问该厂资金紧张期共有几个月?
答案
1.【解析】针对D选项,可知该函数模型为,故不是反比例函数,故选D。
2.【解析】如图所示,人均耕地面积y(单位:公顷人)与总人口.x(单位:人)的函数关系是反比例函数,它的图象在第一象限,所以y随的增大而减小
该村人均耕地面积随总人口的增多而增多"、该村人均耕地面积y与总人口x成正比例"错误;设,把代入得:k=50.,把y=2代入上式的:x=25,若该村人均耕地面积为2公顷,则总人口有100人"错误;把x=50代入上式得:y=1,所以当该村总人口为50人时,人均耕地面积为1公顷"正确.故选D。
3.【解析】设密度与体积V的反比例函数解析式为,把点(5,2)代入解,解得k=10,所以密度与体积V的反比例函数解析式为,把v= 10代入得p = 1 kg/m,故选D。
4.【解析】当F一定时,P与S之间成反比例函数,则函数图象是双曲线,同时自变量是正数.故选C.
5.【解析】设球内气体的气压P(kPa)和气体体积V(m)的关系式为
图象过点(0.8,120),即,在第一象限内,P随v的增大而减小,当时,,故选C
6.【解析】开机加热时每分钟上升10℃,从30℃到100C需要7分钟
设一次函数关系式为:,将(0,30),(7,100)代入得,
,令y=50,解得x=2;设反比例函数关系式为
将(7,100)代入得k=700,
将y=30代入,解得,令y=50,解得x=14
饮水机的一个循环周期为分钟,每一个循环周期内,在及时间段内,水温7超过50℃。逐一分析如下:
选项A:7:20至8:45之间有85分钟.,位于时间段内,故可行;
选项B:7:30至8:45之间有75分钟.,不在及时间段内,故不可行:
选项C:7:45至8:45之间有60分钟.,不在及时间段内,故不可行;
选项D:7:50至8:45之间有55分钟.,不在及时间段内故不可行。
综上所述,四个选项中,唯有7:20符合题意。故选A.
7.【解析】【解析】反比例函数经过点(24,2)
反比例函数的解析式为
当y=6时,解得x=8.
直线与双曲线的交点坐标为(8,6)
正比例函数的解析式为
当时,解得x= 16
当时,解得x=4
当空气中含药量不低于3mg/m时,持续时间可以达到16-4= 12h,
8.【解析】根据题意近视眼镜的度数y(度)与镜片焦距x(米)成反比例,设由于点(0.25,400)在此函数解析式上,
故答案为:
9.【解析】 10
10.【解析】由题意,得,整理可得
11.【解析】(1)易拉罐底面半径和用铝量的关系,易拉罐底面半径为自变量,用铝量为因变量;
(2)当底面半径为2.4cm时,易拉罐的用铝量为5.6cm;
(3)易拉罐底面半径为2.8cm时比较合适,因为此时用铝量较少,成本低;
(4)当易拉罐底面半径在1.6-2.8cm变化时,用铝量随半径的增大而减小,当易拉罐半径在2.8-4.0cm之间变化时,用铝量随半径的增大而增大
12.【解析】
(2)当t=3 h时,v= 100(km/h).随地增大而减小,,即汽车的速度不低于100 km/h
13.【解析】(1)当时,;当时,
(2)当y=0.45时,代入中,得x=240(分钟)=4(小时)
则从药物释放开始,至少需要经过4小时后,生才能进入教室.
14.【解析】(1)分情况讨论:
1.当时
设线段AB对应的函数表达式为y=kx+b
把A(0,10),B(3.4)代入得:
解得:
2.当x>3时,设
把(3.4)代入得:m=34-12
综上所述:当时,y=-2x+10;当x>3时
(2)能;理由如下:
令,则x=12,
3<12<15
故能在15天以内不超过最高允许的1.0mg/L.
15.【解析】(1)当时,设,把(1,200)代入,k=200,即;2.当x=5时,y=40,所以当x>5时,设y=20x+b,则205+b=40,得b=-60,即x>5时,y=20x-60(2)当y=200时,20x-60=200,解得x=13.所以治污改造工程顺利完工后经过13-5=8个月后,该厂利润达200到200万元(3)对于,当y= 100时,x=2;对于y=20x-60,当y = 100时,x=8,所以资金紧张期共有8-2-1=5个月
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
