【百强校】河北省武邑中学人教A版高中数学必修3 第三章 概率小结 -导学案(Word版)
文档属性
| 名称 | 【百强校】河北省武邑中学人教A版高中数学必修3 第三章 概率小结 -导学案(Word版) | 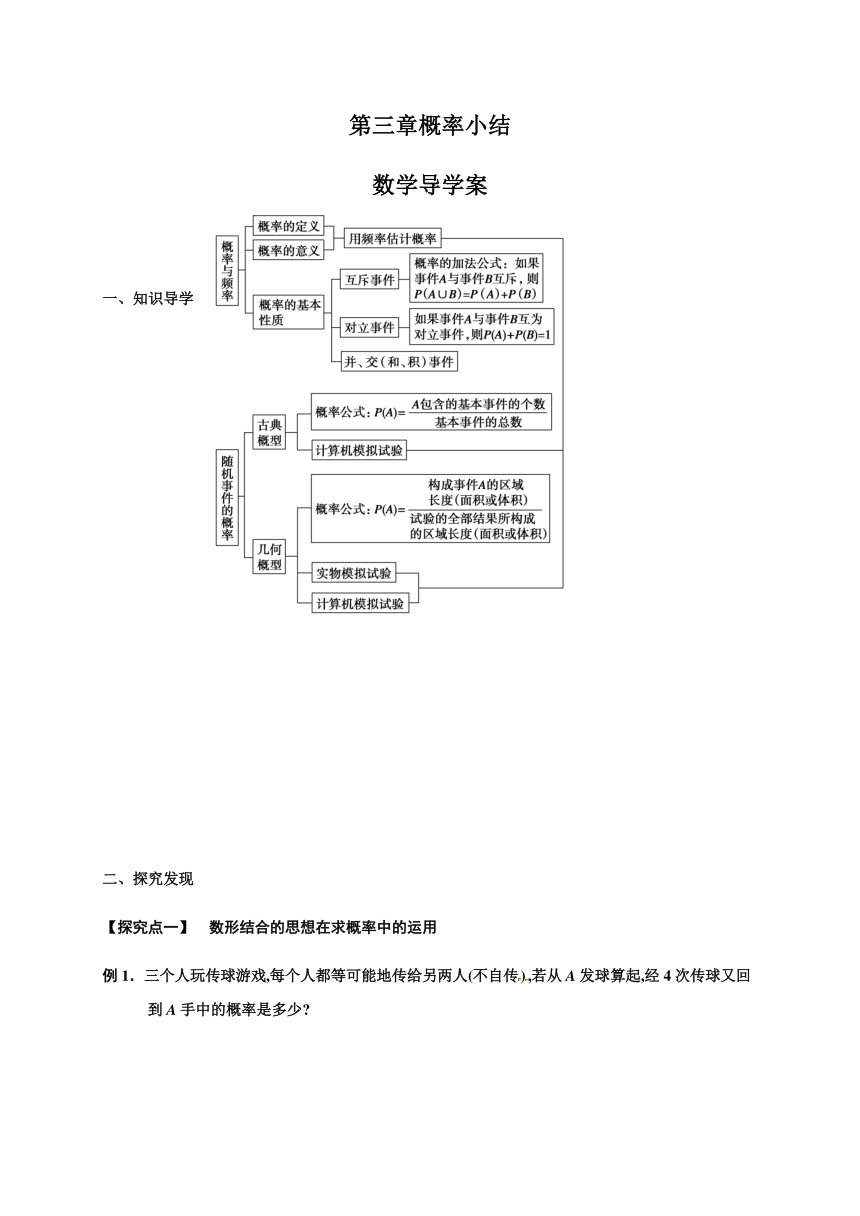 | |
| 格式 | zip | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 21:32:44 | ||
图片预览



文档简介
第三章概率小结
数学导学案
一、知识导学
2、探究发现
【探究点一】 数形结合的思想在求概率中的运用
例1.三个人玩传球游戏,每个人都等可能地传给另两人(不自传),若从A发球算起,经4次传球又回到A手中的概率是多少?
小结 事件个数没有很明显的规律,而且涉及的基本事件又不是太多时,我们可借助树状图法直观地将其表示出来,有利于条理地思考和表达.
跟踪训练1 设M={1,2,3,4,5,6,7,8,9,10},任取x,y∈M,x≠y.求x+y是3的倍数的概率.
【探究点二】正难则反的思想在求概率中的运用
例2.现有8名数理化成绩优秀者,其中A1,A2,A3数学成绩优秀,B1,B2,B3物理成绩优秀,C1,C2化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛.
(1)求C1被选中的概率;
(2)求A1和B1不全被选中的概率.
小结:在求有关事件的概率时,若从正面分析,包含的事件较多或较繁琐,而其反面却较容易入手,这时,可以利用对立事件求解.
跟踪训练2 有4张面值相同的债券,其中有2张中奖债券.
(1)有放回地从债券中任取2张,每次取出1张,计算取出的2张中至少有1张是中奖债券的概率.
(2)无放回地从债券中任取2张,每次取出1张,计算取出的2张中至少有1张是中奖债券的概率.
【探究点三】转化与化归的思想在求概率中的运用
例3.以半径为1的圆内任一点为中点作弦,求弦长超过圆内接等边三角形边长的概率.
小结 在解决与几何概型有关的问题时,注意将试验和事件转化为在“线段、平面区域、空间几何体”上取点的问题.
跟踪训练3 已知正三棱锥S—ABC的底面边长为4,高为3,在正三棱锥内任取一点P,
使得VP—ABC
三、课堂小结:
1.两个事件互斥,它们未必对立;反之,两个事件对立,它们一定互斥.若事件A1,A2,A3,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
2.关于古典概型,必须要解决好下面三个方面的问题:
(1)本试验是否是等可能的?
(2)本试验的基本事件有多少个?
(3)事件A是什么,它包含多少个基本事件?
只有回答好了这三方面的问题,解题才不会出错.
3.几何概型的试验中,事件A的概率P(A)只与子区域A的几何度量(长度、面积或体积)成正比,而与A的位置和形状无关.求试验为几何概型的概率,关键是求得事件所占区域和整个区域Ω的几何度量,然后代入公式即可求解.
4.关于随机数与随机模拟试验问题
随机模拟试验是研究随机事件概率的重要方法,用计算器或计算机模拟试验,首先要把实际问题转化为可以用随机数来模拟试验结果的量,我们可以从以下几个方面考虑:
(1)确定产生随机数组数,如长度型、角度型(一维)一组,面积型(二维)二组.
(2)由所有基本事件总体对应区域确定产生随机数的范围,由事件A发生的条件确定随机数应满足的关系式.
