17.5.2 一元二次方程的应用课件 (共23张PPT)
文档属性
| 名称 | 17.5.2 一元二次方程的应用课件 (共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
17.5.2 一元二次方程的应用2
沪科版 八年级下
第2课时 分式及其它问题
新知导入
问题1.上节课我们主要学习了哪些内容?要注意什么?
答:上节课我们主要学习了一元二次方程实际应用,包含以下两个问题:
1.等积问题;
2.增长率问题.
注意:解一元二次方程得出答案必须检验,要使实际问题有意义.
问题2.我们还可以利用一元二次方程解决哪些实际问题?
新知讲解
一、数位问题:
例1.一个两位数,个位上的数字比十位上的数字大3,且个位上的数字的平方等于这个两位数,求这个两位数.
解:设这个两位数十位上的数字为x,则个位上的数字为(x+3).
由题意得:(x+3)2=10x+(x+3)
整理得:x2-5x+6=0 解得:x1= 2 , x2=3
当x= 2时,x+3=2+3=5,故这个两位数为25;
当x= 3时,x+3=3+3=6,故这个两位数为36.
答:这个两位数为25或36.
新知讲解
归纳小结:解决数位问题的关键是如何用代数式表示这个数,
其公式为:该位上数字×位权+该位上数字×位权+...
如:836=8(百位上数字)×100(位权)+3(十位上数字)×10(位权)+6(个位上数字)×1(位权)
又如:百位上数字为x,十位上数字为y,个位上数字为z.
该三位数可表示为100x+10y+z.
新知讲解
二、分式问题:
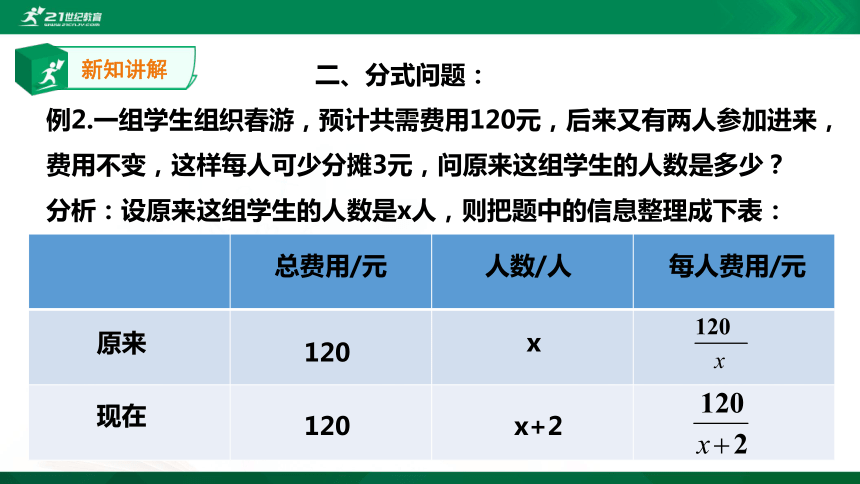
例2.一组学生组织春游,预计共需费用120元,后来又有两人参加进来,费用不变,这样每人可少分摊3元,问原来这组学生的人数是多少?
分析:设原来这组学生的人数是x人,则把题中的信息整理成下表:
总费用/元
人数/人
每人费用/元
原来
现在
120
120
x
x+2
新知讲解
本题的等量关系是:
原来这组学生每人分摊的费用-加人后这组学生每人分摊的费用=3元
解:设原来这组学生的人数是x人,那么这组学生每人分摊的费用为
元,加2人后这组学生每人分摊的费用为 元,
根据增加2人后每人可少分摊3元,得: - =3.
新知讲解
方程两边同乘以x(x+2),整理得:
x2+2x-80=0
解得:x1= 8 , x2=-10
经检验x1= 8 , x2=-10都是原方程的根,但x2=-10不合题意,所以取x= 8.
答:原来这组学生的人数是8人.
新知讲解
归纳小结:列分式解应用题的问题的步骤为:
(1)审题,找出题目中已知与未知;
(2)找出题目中等量关系;
(3)根据题目中等量关系列方程;
(4)解方程;
(5)进行双检;
(6)答.
新知讲解
三、单循环问题:
例3.在抗击新冠疫情进入关键时期,明光市有若干名白衣天使不顾个人安危积极支援武汉,临行前他们相互握手.已知他们相互握手的次数为28次,问明光市有多少名白衣天使支援武汉?
分析:设明光市有x名白衣天使支援武汉,x名白衣天使每人均要和其他
(x-1)名白衣天使握手,是单循环问题.总握手的次数为 次.
本题的等量关系是:
总握手的次数相等.
新知讲解
解:设明光市有x名白衣天使支援武汉
由题意得: =28
整理得:x2-x-56=0
解得:x1= 8, x2=-7
经检验x1= 8, x2=-7都是原方程的根,
但x2=-7不合题意,所以取x=8.
答:明光市有8名白衣天使支援武汉.
新知讲解
归纳小结:单循环问题:
单循环问题与双循环问题只是计算的次数的区别
注意:列方程时,单循环问题重复计算的次数要除以2,双循环则不用除.
课堂练习
1.要组织一次篮球联赛,赛制为单循环形式(每两个队之间都赛一场),计划安排21场比赛,则参赛球队共有( )
A.5支 B.6支 C.7支 D.8支
分析:设参赛球队共有x支
由题意得: =21
整理得:x2-x-42=0
解得:x1= 7, x2=-6经检验x1= 7, x2=-6都是原方程的根,
但x2=-6不合题意,所以取x=7.
C
课堂练习
2.有x支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程中符合题意的是( )
A. B.
C. D.
A
课堂练习
3.一个两位数,两个数字的和为9,如果把个位数字与十位数字互换位置后,再与原数相乘得1458,求这个两位数.
解:设这个两位数十位上的数字为x,则个位上的数字为(9-x).
由题意得:[10x+(9-x)][10(9-x)+x]=1458
整理得:x2-9x+8=0 解得:x1= 1 , x2=8
当x= 1时,9-x=9-1=8,故这个两位数为18;
当x= 8时,9-x=9-8=1,故这个两位数为81.
答:这个两位数为18或81.
课堂练习
4.某市计划种植一批梨树,原计划总产值30万千克,后来改良后每亩产量是原来的1.5倍,总产量比原计划增加了6万千克,种植亩数减少了10亩,则原来平均每亩产量是多少万千克?设原来平均每亩产量是x万千克,根据题意列方程为( )
A. B .
C . D.
A
拓展提高
5.甲乙两个工程小队,甲队修路400米比乙队修路600米所用时间少1天,
已知乙队每天比甲队多修20米,求甲队每天修路的长度.
解:设甲队每天修路的长度为x米,则乙队每天修路的长度为(x+20)米.
由题意得:
方程两边同乘以x(x+20),并整理得:
拓展提高
x2-180x+8000=0
解得:x1= 80 , x2=100
经检验x1= 80 , x2=100都是原方程的根
答:甲队每天修路的长度为80米或100米.
中考链接
6.(南京.中考)刘阿姨到超市购买大米,第1次按原价购买,用了108元.几天后这种大米比打8折还少0.8元出售,她用140元又买了一些,两次一共购买了53千克.问这种大米的原价是多少?
解:设这种大米的原价是x元/千克,由题意得:
解得:x1= 6 , x2=18/53
经检验x1= 6 , x2=18/53都是原方程的根,但x2=18/53不合题意
故取x= 6
答:这种大米的原价是6元/千克
课堂总结
本节课你有什么收获?
本节课我们主要学习了用一元二次方程解决数位问题、单循环问题、分式方程问题等实际问题.
1.其中数位问题公式为:该位上数字×位权+该位上数字×位权+...
2.分式方程问题中找出题目中等量关系,根据题目中等量关系列方程是解题关键,另外要注意进行双检;
3.单循环问题:单循环问题与双循环问题只是计算的次数的区别,注意:列方程时,单循环问题重复计算的次数要除以2,双循环则不用除.
板书设计
17.5.2一元二次方程的应用2
1.数位问题
2.分式方程问题
3.单循环问题
作业布置
课本 P49-50页
练习题6--10题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
17.5.2 一元二次方程的应用2
沪科版 八年级下
第2课时 分式及其它问题
新知导入
问题1.上节课我们主要学习了哪些内容?要注意什么?
答:上节课我们主要学习了一元二次方程实际应用,包含以下两个问题:
1.等积问题;
2.增长率问题.
注意:解一元二次方程得出答案必须检验,要使实际问题有意义.
问题2.我们还可以利用一元二次方程解决哪些实际问题?
新知讲解
一、数位问题:
例1.一个两位数,个位上的数字比十位上的数字大3,且个位上的数字的平方等于这个两位数,求这个两位数.
解:设这个两位数十位上的数字为x,则个位上的数字为(x+3).
由题意得:(x+3)2=10x+(x+3)
整理得:x2-5x+6=0 解得:x1= 2 , x2=3
当x= 2时,x+3=2+3=5,故这个两位数为25;
当x= 3时,x+3=3+3=6,故这个两位数为36.
答:这个两位数为25或36.
新知讲解
归纳小结:解决数位问题的关键是如何用代数式表示这个数,
其公式为:该位上数字×位权+该位上数字×位权+...
如:836=8(百位上数字)×100(位权)+3(十位上数字)×10(位权)+6(个位上数字)×1(位权)
又如:百位上数字为x,十位上数字为y,个位上数字为z.
该三位数可表示为100x+10y+z.
新知讲解
二、分式问题:
例2.一组学生组织春游,预计共需费用120元,后来又有两人参加进来,费用不变,这样每人可少分摊3元,问原来这组学生的人数是多少?
分析:设原来这组学生的人数是x人,则把题中的信息整理成下表:
总费用/元
人数/人
每人费用/元
原来
现在
120
120
x
x+2
新知讲解
本题的等量关系是:
原来这组学生每人分摊的费用-加人后这组学生每人分摊的费用=3元
解:设原来这组学生的人数是x人,那么这组学生每人分摊的费用为
元,加2人后这组学生每人分摊的费用为 元,
根据增加2人后每人可少分摊3元,得: - =3.
新知讲解
方程两边同乘以x(x+2),整理得:
x2+2x-80=0
解得:x1= 8 , x2=-10
经检验x1= 8 , x2=-10都是原方程的根,但x2=-10不合题意,所以取x= 8.
答:原来这组学生的人数是8人.
新知讲解
归纳小结:列分式解应用题的问题的步骤为:
(1)审题,找出题目中已知与未知;
(2)找出题目中等量关系;
(3)根据题目中等量关系列方程;
(4)解方程;
(5)进行双检;
(6)答.
新知讲解
三、单循环问题:
例3.在抗击新冠疫情进入关键时期,明光市有若干名白衣天使不顾个人安危积极支援武汉,临行前他们相互握手.已知他们相互握手的次数为28次,问明光市有多少名白衣天使支援武汉?
分析:设明光市有x名白衣天使支援武汉,x名白衣天使每人均要和其他
(x-1)名白衣天使握手,是单循环问题.总握手的次数为 次.
本题的等量关系是:
总握手的次数相等.
新知讲解
解:设明光市有x名白衣天使支援武汉
由题意得: =28
整理得:x2-x-56=0
解得:x1= 8, x2=-7
经检验x1= 8, x2=-7都是原方程的根,
但x2=-7不合题意,所以取x=8.
答:明光市有8名白衣天使支援武汉.
新知讲解
归纳小结:单循环问题:
单循环问题与双循环问题只是计算的次数的区别
注意:列方程时,单循环问题重复计算的次数要除以2,双循环则不用除.
课堂练习
1.要组织一次篮球联赛,赛制为单循环形式(每两个队之间都赛一场),计划安排21场比赛,则参赛球队共有( )
A.5支 B.6支 C.7支 D.8支
分析:设参赛球队共有x支
由题意得: =21
整理得:x2-x-42=0
解得:x1= 7, x2=-6经检验x1= 7, x2=-6都是原方程的根,
但x2=-6不合题意,所以取x=7.
C
课堂练习
2.有x支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程中符合题意的是( )
A. B.
C. D.
A
课堂练习
3.一个两位数,两个数字的和为9,如果把个位数字与十位数字互换位置后,再与原数相乘得1458,求这个两位数.
解:设这个两位数十位上的数字为x,则个位上的数字为(9-x).
由题意得:[10x+(9-x)][10(9-x)+x]=1458
整理得:x2-9x+8=0 解得:x1= 1 , x2=8
当x= 1时,9-x=9-1=8,故这个两位数为18;
当x= 8时,9-x=9-8=1,故这个两位数为81.
答:这个两位数为18或81.
课堂练习
4.某市计划种植一批梨树,原计划总产值30万千克,后来改良后每亩产量是原来的1.5倍,总产量比原计划增加了6万千克,种植亩数减少了10亩,则原来平均每亩产量是多少万千克?设原来平均每亩产量是x万千克,根据题意列方程为( )
A. B .
C . D.
A
拓展提高
5.甲乙两个工程小队,甲队修路400米比乙队修路600米所用时间少1天,
已知乙队每天比甲队多修20米,求甲队每天修路的长度.
解:设甲队每天修路的长度为x米,则乙队每天修路的长度为(x+20)米.
由题意得:
方程两边同乘以x(x+20),并整理得:
拓展提高
x2-180x+8000=0
解得:x1= 80 , x2=100
经检验x1= 80 , x2=100都是原方程的根
答:甲队每天修路的长度为80米或100米.
中考链接
6.(南京.中考)刘阿姨到超市购买大米,第1次按原价购买,用了108元.几天后这种大米比打8折还少0.8元出售,她用140元又买了一些,两次一共购买了53千克.问这种大米的原价是多少?
解:设这种大米的原价是x元/千克,由题意得:
解得:x1= 6 , x2=18/53
经检验x1= 6 , x2=18/53都是原方程的根,但x2=18/53不合题意
故取x= 6
答:这种大米的原价是6元/千克
课堂总结
本节课你有什么收获?
本节课我们主要学习了用一元二次方程解决数位问题、单循环问题、分式方程问题等实际问题.
1.其中数位问题公式为:该位上数字×位权+该位上数字×位权+...
2.分式方程问题中找出题目中等量关系,根据题目中等量关系列方程是解题关键,另外要注意进行双检;
3.单循环问题:单循环问题与双循环问题只是计算的次数的区别,注意:列方程时,单循环问题重复计算的次数要除以2,双循环则不用除.
板书设计
17.5.2一元二次方程的应用2
1.数位问题
2.分式方程问题
3.单循环问题
作业布置
课本 P49-50页
练习题6--10题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
