鲁教版(五四制)七年级数学下册7.4 二元一次方程与一次函数 第二课时 课件(15张PPT)
文档属性
| 名称 | 鲁教版(五四制)七年级数学下册7.4 二元一次方程与一次函数 第二课时 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 434.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-11 19:19:09 | ||
图片预览





文档简介
(共15张PPT)
7.4 二元一次方程与一次函数
第2课时
Contents
目录
01
02
学习目标
新知探究
随堂练习
课堂小结
旧知回顾
二元一次方程与一次函数之间有什么联系?
二元一次方程的解就是相应一次函数图象上的点的坐标;
一次函数图象上的点的坐标就是相应二元一次方程的解.
从图形的角度看,确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;
解一个二元一次方程组,就相当于确定相应两条直线交点的坐标.
1、进一步理解二元一次方程与一次函数的关系;
2、掌握利用二元一次方程组确定一次函数的表达式.
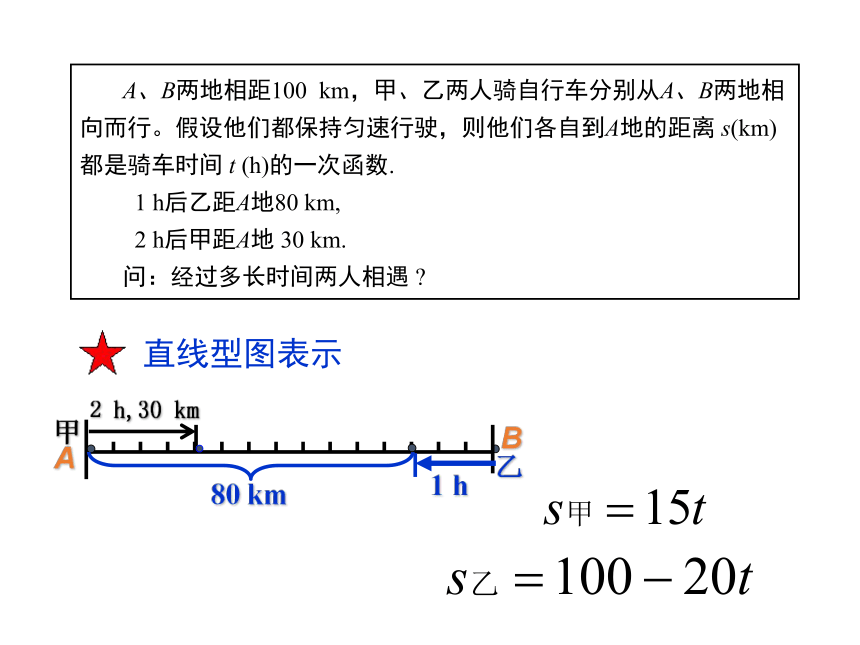
A、B两地相距100 km,甲、乙两人骑自行车分别从A、B两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离 s(km)都是骑车时间 t (h)的一次函数.
1 h后乙距A地80 km,
2 h后甲距A地 30 km.
问:经过多长时间两人相遇 ?
议一议
请你自己先想一想,你是怎么做的呢?
A、B两地相距100 km,甲、乙两人骑自行车分别从A、B两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离 s(km)都是骑车时间 t (h)的一次函数.
1 h后乙距A地80 km,
2 h后甲距A地 30 km.
问:经过多长时间两人相遇 ?
100
80
60
40
20
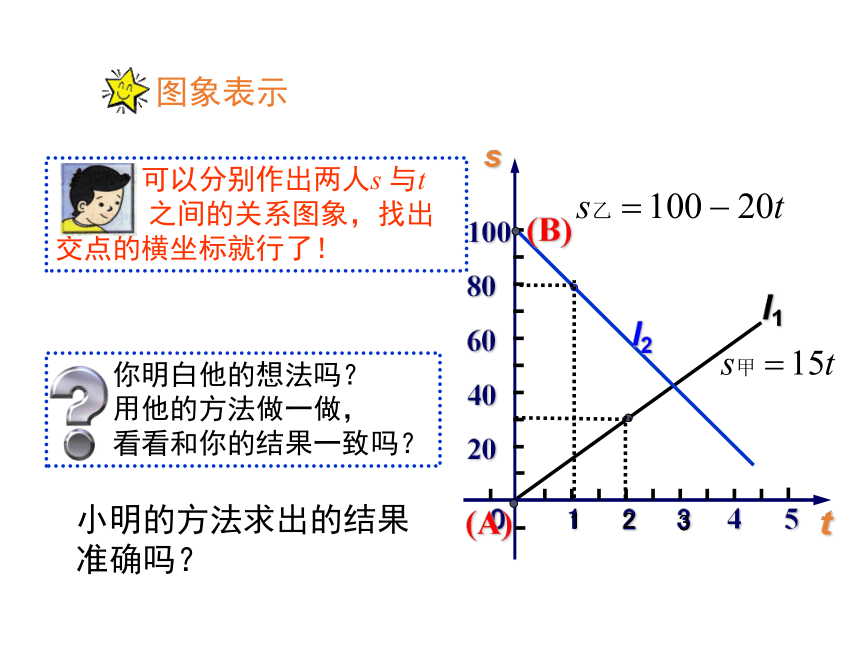
小明的方法求出的结果准确吗?
1
2
3
5
求出s与t之间的关系式,联立解方程组
对于乙,s是t的一次函数,可设 s=kt+b。
当t=0时,s=100;当t=1时,s=80。
将它们分别代入s=kt+b中,可以求出k、b的值,
也即可以求出乙s与t之间的函数表达式。
同样可求出甲s与t之间的函数表达式。
再联立这两个表达式,求解方程组就行了。
用方程解行程问题
1 h后乙距A地80 km,即乙的速度是 20 km/h,
2 h后甲距A地 30 km,故甲的速度是 15km/h,
由此可求出甲、乙两人的速度, 以及……
?t≈2.86
设同时出发后t时相遇,则
15t+20t=100
用一元一次方程的方法可以解决问题
用图象法可以解决问题
用方程组的方法可以解决问题
用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法。
在以上的解题过程中你受到什么启发?
例:某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数,现知李明带了60kg的行李,交了行李费5元,王华带了90kg的行李,交了行李费10元. (1)写出y与x之间的函数表达式 (2)旅客最多可免费携带多少千克的行李?
解:(1)设y=kx+b,根据题意,得
解得
所以
(2)当y=0时,解得x=30
所以旅客最多可以免费携带30 kg的行李。
像本例这样,先设出函数表达式,再根据所给条件确定表达式中未知数的系数,从而得到函数表达式的方法,叫做待定系数法.
小结
利用二元一次方程组确定一次函数的表达式是求一次函数表达式的主要方法,一般步骤如下:
(1)设出函数表达式: y=kx+b;
(2)把已知条件代入,得到关于k、b的方程组;
(3)解方程组,求出k、b的值;
(4)写出其表达式.
知识升华
(A) 4 (B) 5 (C) 6 (D) 7
C
1 -9
3.求两条直线y=3x-2与y=-2x+4和x轴所围成的三角形的面积.
1.已知一次函数y=kx-5与y=3x+b的图象交点为P(2,﹣3),则k= ,b= .
2.已知一次函数y=2x+a与y=﹣x+b的图象都经过点A(﹣2,0),且与y轴分别交于B,C两点,则△ABC的面积是( )
1、方法归纳
用图象法解二元一次方程组
优点:方法简便,形象直观;体现了数形结合思想.
不足:一般情况下求出的是近似数;要想精确还要用代 数方法,进行细致计算.
2、待定系数法求一次函数的表达式
课本习题7.8
7.4 二元一次方程与一次函数
第2课时
Contents
目录
01
02
学习目标
新知探究
随堂练习
课堂小结
旧知回顾
二元一次方程与一次函数之间有什么联系?
二元一次方程的解就是相应一次函数图象上的点的坐标;
一次函数图象上的点的坐标就是相应二元一次方程的解.
从图形的角度看,确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;
解一个二元一次方程组,就相当于确定相应两条直线交点的坐标.
1、进一步理解二元一次方程与一次函数的关系;
2、掌握利用二元一次方程组确定一次函数的表达式.
A、B两地相距100 km,甲、乙两人骑自行车分别从A、B两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离 s(km)都是骑车时间 t (h)的一次函数.
1 h后乙距A地80 km,
2 h后甲距A地 30 km.
问:经过多长时间两人相遇 ?
议一议
请你自己先想一想,你是怎么做的呢?
A、B两地相距100 km,甲、乙两人骑自行车分别从A、B两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离 s(km)都是骑车时间 t (h)的一次函数.
1 h后乙距A地80 km,
2 h后甲距A地 30 km.
问:经过多长时间两人相遇 ?
100
80
60
40
20
小明的方法求出的结果准确吗?
1
2
3
5
求出s与t之间的关系式,联立解方程组
对于乙,s是t的一次函数,可设 s=kt+b。
当t=0时,s=100;当t=1时,s=80。
将它们分别代入s=kt+b中,可以求出k、b的值,
也即可以求出乙s与t之间的函数表达式。
同样可求出甲s与t之间的函数表达式。
再联立这两个表达式,求解方程组就行了。
用方程解行程问题
1 h后乙距A地80 km,即乙的速度是 20 km/h,
2 h后甲距A地 30 km,故甲的速度是 15km/h,
由此可求出甲、乙两人的速度, 以及……
?t≈2.86
设同时出发后t时相遇,则
15t+20t=100
用一元一次方程的方法可以解决问题
用图象法可以解决问题
用方程组的方法可以解决问题
用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法。
在以上的解题过程中你受到什么启发?
例:某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数,现知李明带了60kg的行李,交了行李费5元,王华带了90kg的行李,交了行李费10元. (1)写出y与x之间的函数表达式 (2)旅客最多可免费携带多少千克的行李?
解:(1)设y=kx+b,根据题意,得
解得
所以
(2)当y=0时,解得x=30
所以旅客最多可以免费携带30 kg的行李。
像本例这样,先设出函数表达式,再根据所给条件确定表达式中未知数的系数,从而得到函数表达式的方法,叫做待定系数法.
小结
利用二元一次方程组确定一次函数的表达式是求一次函数表达式的主要方法,一般步骤如下:
(1)设出函数表达式: y=kx+b;
(2)把已知条件代入,得到关于k、b的方程组;
(3)解方程组,求出k、b的值;
(4)写出其表达式.
知识升华
(A) 4 (B) 5 (C) 6 (D) 7
C
1 -9
3.求两条直线y=3x-2与y=-2x+4和x轴所围成的三角形的面积.
1.已知一次函数y=kx-5与y=3x+b的图象交点为P(2,﹣3),则k= ,b= .
2.已知一次函数y=2x+a与y=﹣x+b的图象都经过点A(﹣2,0),且与y轴分别交于B,C两点,则△ABC的面积是( )
1、方法归纳
用图象法解二元一次方程组
优点:方法简便,形象直观;体现了数形结合思想.
不足:一般情况下求出的是近似数;要想精确还要用代 数方法,进行细致计算.
2、待定系数法求一次函数的表达式
课本习题7.8
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
