新人教A版必修5 高中数学第二章数列 章末归纳整合 课件(共37张PPT)
文档属性
| 名称 | 新人教A版必修5 高中数学第二章数列 章末归纳整合 课件(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 498.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
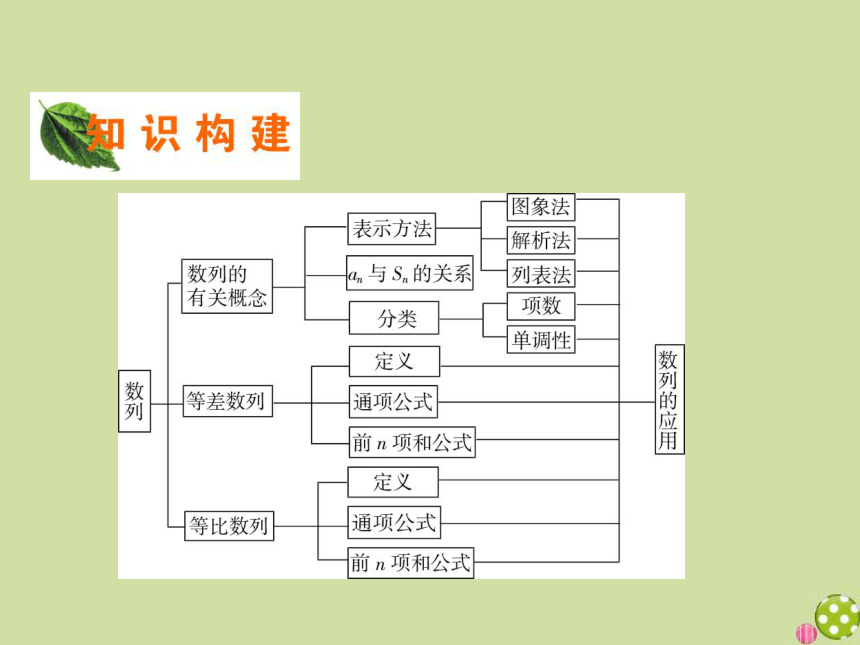
章末归纳整合
整体思想是从问题的整体结构出发,实施整体变形、运算的思想,整体思想的灵活运用通常能将问题由多方向简化,使问题变得明朗,简捷.
整体思想
【例1】 某等差数列的前四项之和为-4,最后四项之和为36,所有项之和为36,则此数列共有______项.
【点评】本题考查等差数列的求和公式,涉及等差数列的性质,由题意可得a1+a2+a3+a4=-4,an+an-1+an-2+an-3=36,两式相加可得a1+an的值,代入求和公式可得关于n的方程,解方程可得.
一个等差数列前4项之和为26,最后4项之和为110,所有项之和为187,则它的项数为______.
【答案】11
数列是特殊的函数,用函数的观点认识数列和处理数列问题,既有利于理解和掌握数列的基本概念和性质,又利于解决问题.等差(比)数列的通项公式和求和公式中的五个量中,已知其中任意三个,通过解方程可求其余两个.
方程思想
【例2】 设递增等差数列{an}的前n项和为Sn,已知a3=1,a4是a3和a7的等比中项.
(1)求数列{an}的通项公式;
(2)求数列{an}的前n项和Sn.
【点评】本题考查等差数列的性质和应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
在解决数学问题时,应注意问题的层次性,即考虑到问题的方方面面,在讨论时应考虑全面,做到不重不漏,这是历年高考的重点.
分类讨论思想
【分析】(1)运用等差数列的通项公式与求和公式,根据条件列方程,求出首项和公差,得到通项an.运用n=1时,b1=T1,n>1时,bn=Tn-Tn-1,求出bn.
(2)写出cn,然后运用分组求和,一组为等差数列,一组为等比数列,分别应用求和公式化简即可.
【点评】本题主要考查等差数列和等比数列的通项与求和公式的运用,考查方程的思想在数列中的运用,同时考查数列的通项与前n项和的关系式,考查数列的求和方法,是一道综合题.
【解析】(1)∵an=an-1·3n-1,两边取以3为底的对数得log3an=log3an-1+(n-1),
∴log3an-log3an-1=n-1.
log3a2-log3a1=1,
log3a3-log3a2=2,
…,
log3an-log3an-1=n-1,
数列在高考中主要考查以下三个方面:1.等差(比)数列的通项公式及前n项和公式;2.等差、等比数列的综合应用;3.数列的实际应用.主要考查等差、等比数列的定义、通项公式及前n和公式,重在考查基础知识和运算能力,是每年必考内容之一.考查方式可以是选择题、填空题和解答题.
1.(2018年新课标Ⅰ)记Sn为等差数列{an}的前n项和.若3S3=S2+S4,a1=2,则a5=( )
A.-12 B.-10
C.10 D.12
【答案】B
【答案】D
3.(2017年新课标Ⅱ)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A.1盏 B.3盏
C.5盏 D.9盏
【答案】B
4.(2018年新课标Ⅰ)记Sn为数列的前n项和.若Sn=2an+1,则S6=________.
【答案】-63
8.(2017年天津)已知{an}为等差数列,前n项和为Sn (n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(1)求{an}和{bn}的通项公式;
(2)求数列{a2nbn}的前n项和(n∈N*).
【解析】(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q.
由已知b2+b3=12,得b1(q+q2)=12,而b1=2,所以q2+q-6=0.
又因为q>0,解得q=2,所以bn=2n.
由b3=a4-2a1,可得3d-a1=8,①
由S11=11b4,可得a1+5d=16.②
联立①②,解得a1=1,d=3,由此可得an=3n-2.
所以{an}的通项公式为an=3n-2,{bn}的通项公式为bn=2n.
章末归纳整合
整体思想是从问题的整体结构出发,实施整体变形、运算的思想,整体思想的灵活运用通常能将问题由多方向简化,使问题变得明朗,简捷.
整体思想
【例1】 某等差数列的前四项之和为-4,最后四项之和为36,所有项之和为36,则此数列共有______项.
【点评】本题考查等差数列的求和公式,涉及等差数列的性质,由题意可得a1+a2+a3+a4=-4,an+an-1+an-2+an-3=36,两式相加可得a1+an的值,代入求和公式可得关于n的方程,解方程可得.
一个等差数列前4项之和为26,最后4项之和为110,所有项之和为187,则它的项数为______.
【答案】11
数列是特殊的函数,用函数的观点认识数列和处理数列问题,既有利于理解和掌握数列的基本概念和性质,又利于解决问题.等差(比)数列的通项公式和求和公式中的五个量中,已知其中任意三个,通过解方程可求其余两个.
方程思想
【例2】 设递增等差数列{an}的前n项和为Sn,已知a3=1,a4是a3和a7的等比中项.
(1)求数列{an}的通项公式;
(2)求数列{an}的前n项和Sn.
【点评】本题考查等差数列的性质和应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
在解决数学问题时,应注意问题的层次性,即考虑到问题的方方面面,在讨论时应考虑全面,做到不重不漏,这是历年高考的重点.
分类讨论思想
【分析】(1)运用等差数列的通项公式与求和公式,根据条件列方程,求出首项和公差,得到通项an.运用n=1时,b1=T1,n>1时,bn=Tn-Tn-1,求出bn.
(2)写出cn,然后运用分组求和,一组为等差数列,一组为等比数列,分别应用求和公式化简即可.
【点评】本题主要考查等差数列和等比数列的通项与求和公式的运用,考查方程的思想在数列中的运用,同时考查数列的通项与前n项和的关系式,考查数列的求和方法,是一道综合题.
【解析】(1)∵an=an-1·3n-1,两边取以3为底的对数得log3an=log3an-1+(n-1),
∴log3an-log3an-1=n-1.
log3a2-log3a1=1,
log3a3-log3a2=2,
…,
log3an-log3an-1=n-1,
数列在高考中主要考查以下三个方面:1.等差(比)数列的通项公式及前n项和公式;2.等差、等比数列的综合应用;3.数列的实际应用.主要考查等差、等比数列的定义、通项公式及前n和公式,重在考查基础知识和运算能力,是每年必考内容之一.考查方式可以是选择题、填空题和解答题.
1.(2018年新课标Ⅰ)记Sn为等差数列{an}的前n项和.若3S3=S2+S4,a1=2,则a5=( )
A.-12 B.-10
C.10 D.12
【答案】B
【答案】D
3.(2017年新课标Ⅱ)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A.1盏 B.3盏
C.5盏 D.9盏
【答案】B
4.(2018年新课标Ⅰ)记Sn为数列的前n项和.若Sn=2an+1,则S6=________.
【答案】-63
8.(2017年天津)已知{an}为等差数列,前n项和为Sn (n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(1)求{an}和{bn}的通项公式;
(2)求数列{a2nbn}的前n项和(n∈N*).
【解析】(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q.
由已知b2+b3=12,得b1(q+q2)=12,而b1=2,所以q2+q-6=0.
又因为q>0,解得q=2,所以bn=2n.
由b3=a4-2a1,可得3d-a1=8,①
由S11=11b4,可得a1+5d=16.②
联立①②,解得a1=1,d=3,由此可得an=3n-2.
所以{an}的通项公式为an=3n-2,{bn}的通项公式为bn=2n.
