人教版 八年级数学(下) 18.1 平行四边形 同步练习题 (含解析)
文档属性
| 名称 | 人教版 八年级数学(下) 18.1 平行四边形 同步练习题 (含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 17:31:25 | ||
图片预览


文档简介
人教新版 八年级(下) 18.1 平行四边形 同步练习
一.选择题(共10小题)
1.如图,中,点、分别在、边上,,,,则
A.4 B.3 C.2 D.5
2.如图,在平行四边形中,,,、的平分线分别交于点、,则的长是
A.3 B.2 C.1.5 D.1
3.下列说法错误的是
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
4.已知四边形,以下有四组条件:(1),;(2),;(3),;(4),.能判定四边形是平行四边形的有
A.1组 B.2组 C.3组 D.4组
5.如图,在中,对角线与相交于点,是边的中点,连接,若,,则
A. B. C. D.
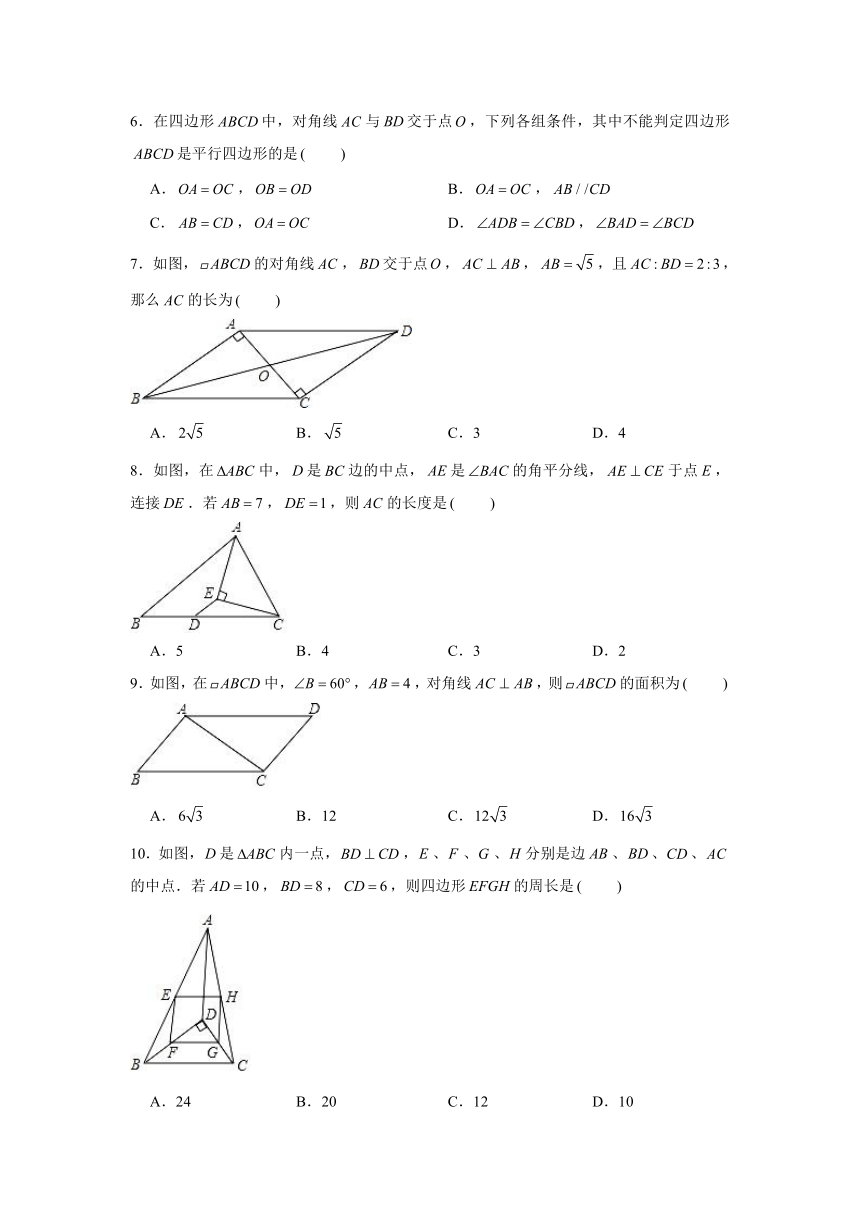
6.在四边形中,对角线与交于点,下列各组条件,其中不能判定四边形是平行四边形的是
A., B.,
C., D.,
7.如图,的对角线,交于点,,,且,那么的长为
A. B. C.3 D.4
8.如图,在中,是边的中点,是的角平分线,于点,连接.若,,则的长度是
A.5 B.4 C.3 D.2
9.如图,在中,,,对角线,则的面积为
A. B.12 C. D.
10.如图,是内一点,,、、、分别是边、、、的中点.若,,,则四边形的周长是
A.24 B.20 C.12 D.10
二.填空题(共8小题)
11.已知直线,与之间的距离为5,与之间有一点,点到的距离是2,则点到的距离是 .
12.如图,平行四边形中,,;,平分,交于点,交延长线于点,则的长度为 .
13.如图,在中,对角线与相交于点,,交于,若,,则的长是 .
14.如图,的对角线相交于点,且,过点作,交于点.若,的周长为9,则 .
15.在中,,,连接,若,则线段的长为 .
16.如图,在平行四边形中,,.的平分线交于点,交的延长线于点,则的长为 .
17.如图,在四边形中,,、分别为线段、上的动点(含端点,但点不与点重合),、分别为、的中点,若,,则长度的最大值为 .
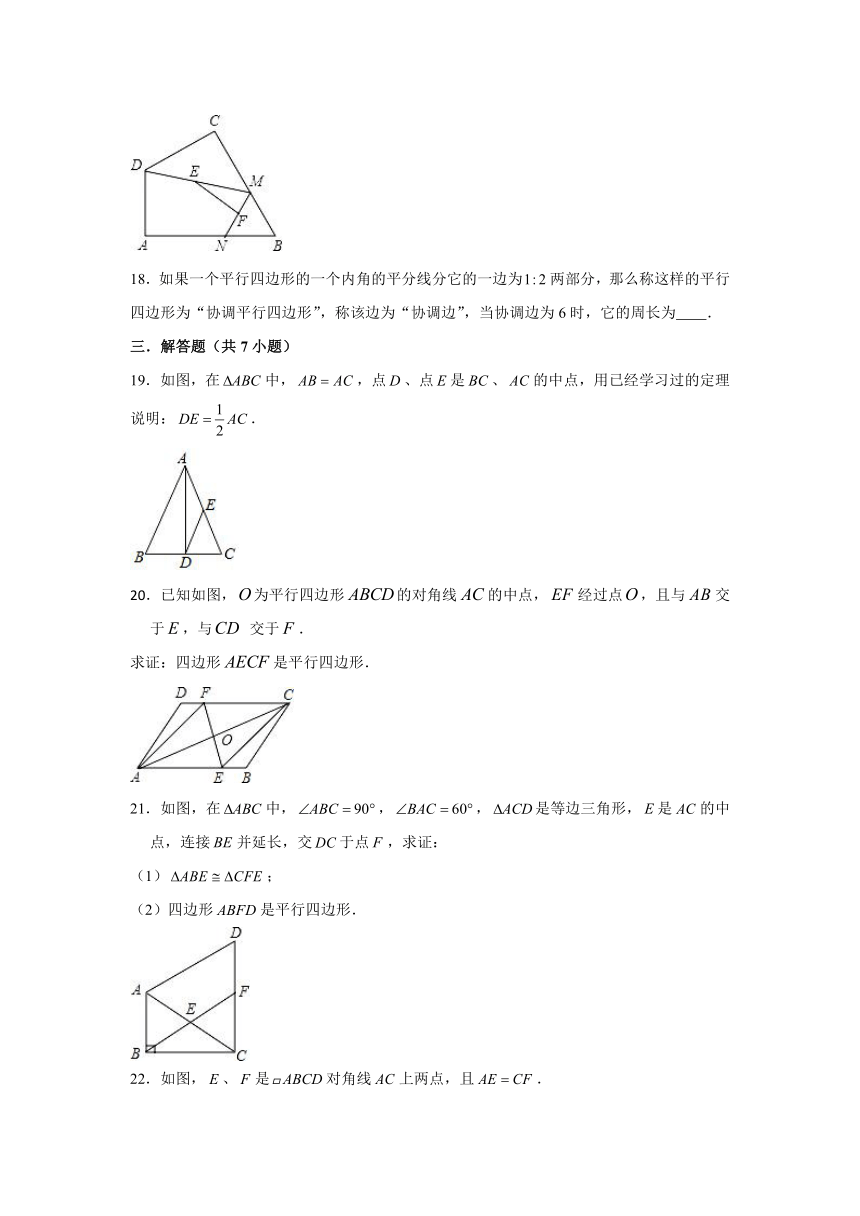
18.如果一个平行四边形的一个内角的平分线分它的一边为两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”,当协调边为6时,它的周长为 .
三.解答题(共7小题)
19.如图,在中,,点、点是、的中点,用已经学习过的定理说明:.
20.已知如图,为平行四边形的对角线的中点,经过点,且与交于,与 交于.
求证:四边形是平行四边形.
21.如图,在中,,,是等边三角形,是的中点,连接并延长,交于点,求证:
(1);
(2)四边形是平行四边形.
22.如图,、是对角线上两点,且.
(1)求证:四边形是平行四边形.
(2)如果把条件改为,试问四边形还是平行四边形吗?为什么?
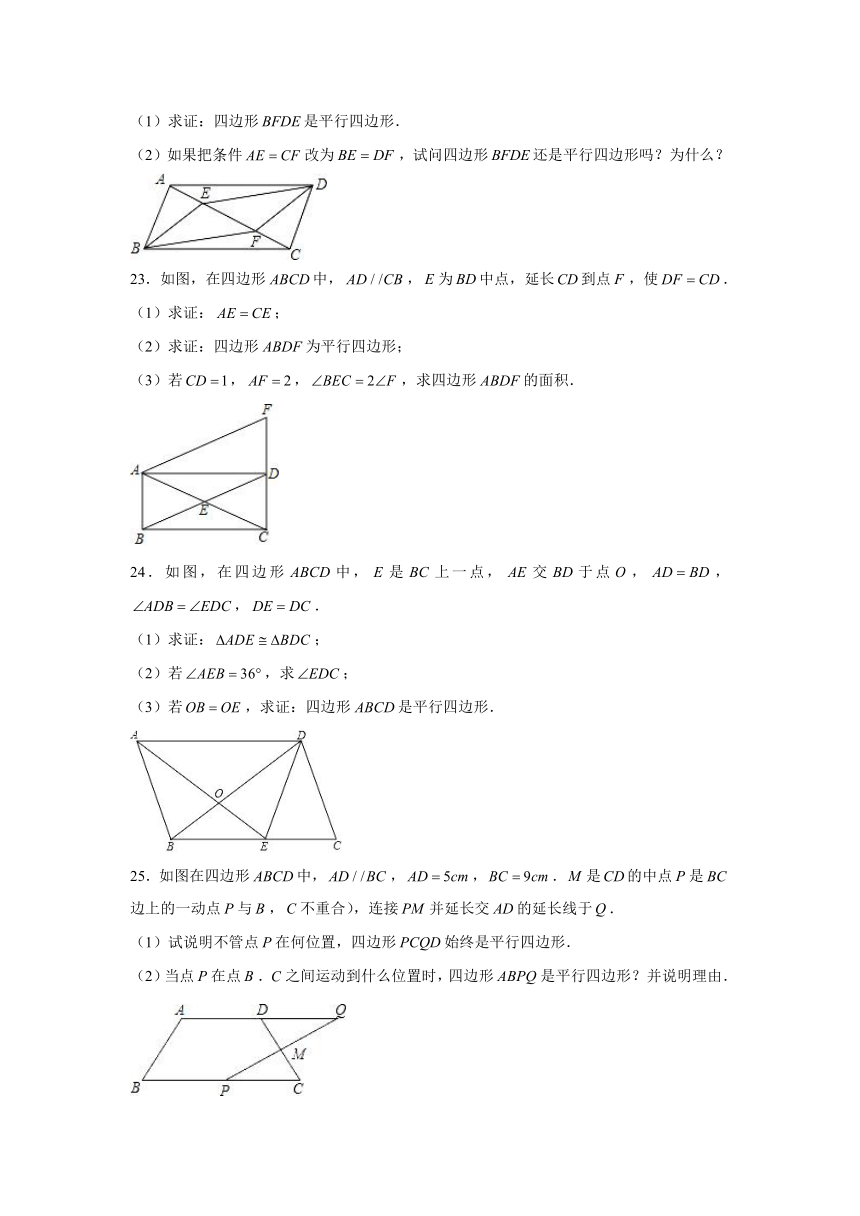
23.如图,在四边形中,,为中点,延长到点,使.
(1)求证:;
(2)求证:四边形为平行四边形;
(3)若,,,求四边形的面积.
24.如图,在四边形中,是上一点,交于点,,,.
(1)求证:;
(2)若,求;
(3)若,求证:四边形是平行四边形.
25.如图在四边形中,,,.是的中点是边上的一动点与,不重合),连接并延长交的延长线于.
(1)试说明不管点在何位置,四边形始终是平行四边形.
(2)当点在点.之间运动到什么位置时,四边形是平行四边形?并说明理由.
参考答案
一.选择题(共10小题)
1.如图,中,点、分别在、边上,,,,则
A.4 B.3 C.2 D.5
【解答】解:,,
是的中位线,
,
,
故选:.
2.如图,在平行四边形中,,,、的平分线分别交于点、,则的长是
A.3 B.2 C.1.5 D.1
【解答】解:平行四边形,
,
又平分,
,
,
,
同理可证:,
.
故选:.
3.下列说法错误的是
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
【解答】解:
由平行四边形的判定方法可知:两组对边分别平行、两组对边分别相等、一组对边平行且相等的四边形是平行四边形,故、、说法正确,
当一组对边平行,另一组对边相等时,该四边形可能为等腰梯形,故是说法错误的,
故选:.
4.已知四边形,以下有四组条件:(1),;(2),;(3),;(4),.能判定四边形是平行四边形的有
A.1组 B.2组 C.3组 D.4组
【解答】解:(1),,
四边形是平行四边形;
(2),,
四边形不一定是平行四边形;
(3),,
四边形不一定是平行四边形;
(4),,
四边形是平行四边形;
故选:.
5.如图,在中,对角线与相交于点,是边的中点,连接,若,,则
A. B. C. D.
【解答】解:四边形是平行四边形,
,,
,,
,
,
,
故选:.
6.在四边形中,对角线与交于点,下列各组条件,其中不能判定四边形是平行四边形的是
A., B.,
C., D.,
【解答】解:、,,
四边形是平行四边形.故能判定这个四边形是平行四边形;
、,,
四边形是平行四边形.故能判定这个四边形是平行四边形;
、,,
四边形不是平行四边形.故不能判定这个四边形是平行四边形;
、,,
四边形是平行四边形,故能判定这个四边形是平行四边形.
故选:.
7.如图,的对角线,交于点,,,且,那么的长为
A. B. C.3 D.4
【解答】解:四边形是平行四边形,
,,
,
,设,,
,
,
,
,
,
,
,
.
故选:.
8.如图,在中,是边的中点,是的角平分线,于点,连接.若,,则的长度是
A.5 B.4 C.3 D.2
【解答】解:延长,交于点.
平分,,
,,
在与中,,
,
,,
又是中点,
,
是的中位线,
.
;
故选:.
9.如图,在中,,,对角线,则的面积为
A. B.12 C. D.
【解答】解:在中,,,对角线,
,
的面积为,
故选:.
10.如图,是内一点,,、、、分别是边、、、的中点.若,,,则四边形的周长是
A.24 B.20 C.12 D.10
【解答】解:,,,
,
、、、分别是、、、的中点,
,,
四边形的周长,
又,
四边形的周长,
故选:.
二.填空题(共8小题)
11.已知直线,与之间的距离为5,与之间有一点,点到的距离是2,则点到的距离是 3 .
【解答】解:直线,与之间的距离为5,与之间有一点,点到的距离是2,
点到的距离是,
故答案为:3.
12.如图,平行四边形中,,;,平分,交于点,交延长线于点,则的长度为 .
【解答】解:平行四边形,
,
,
平分,
,
,
,
同理可得:,
,,
.,
,,
,
故答案为:.
13.如图,在中,对角线与相交于点,,交于,若,,则的长是 10 .
【解答】解:四边形是平行四边形,
,,
,
,
是的中位线,
,
.
,
,
,
,
,
故答案为:10.
14.如图,的对角线相交于点,且,过点作,交于点.若,的周长为9,则 6 .
【解答】解:是平行四边形,
,,,
,
.
的周长,
,
,
故答案为6.
15.在中,,,连接,若,则线段的长为 4或8 .
【解答】解:作于,如图所示:
,
,
,,
,或,
四边形是平行四边形,
或8;
故答案为:4或8.
16.如图,在平行四边形中,,.的平分线交于点,交的延长线于点,则的长为 3 .
【解答】解:在平行四边形中,,,
,,,
,
平分,
,
,
,
,
,
,
又,,
,
,
故答案为:3.
17.如图,在四边形中,,、分别为线段、上的动点(含端点,但点不与点重合),、分别为、的中点,若,,则长度的最大值为 2 .
【解答】解:连接、,
在中,,
点、分别为、的中点,
,
由题意得,当点与点重合时,最大,
的最大值是4,
长度的最大值是2,
故答案为:2.
18.如果一个平行四边形的一个内角的平分线分它的一边为两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”,当协调边为6时,它的周长为 16或20 .
【解答】解:如图所示:①当,时,
四边形是平行四边形,
,,,
,
平分,
,
,
,
平行四边形的周长;
②当,时,
同理得:,
平行四边形的周长;
故答案为:16或20.
三.解答题(共7小题)
19.如图,在中,,点、点是、的中点,用已经学习过的定理说明:.
【解答】解:中,,点是的中点,
,
为的中点,
.
20.已知如图,为平行四边形的对角线的中点,经过点,且与交于,与 交于.
求证:四边形是平行四边形.
【解答】证明:平行四边形中,
,
又,,
,
,
四边形是平行四边形.
21.如图,在中,,,是等边三角形,是的中点,连接并延长,交于点,求证:
(1);
(2)四边形是平行四边形.
【解答】证明:(1)是等边三角形,
,
,
,
在与中,
,
;
(2)是的中点,
,
,
是等边三角形,
是等边三角形,
,
是等边三角形,
,
,
,
,
,
四边形是平行四边形.
22.如图,、是对角线上两点,且.
(1)求证:四边形是平行四边形.
(2)如果把条件改为,试问四边形还是平行四边形吗?为什么?
【解答】(1)证明:连接,交于点.
是平行四边形
(平行四边形的对角线互相平分)
又
,即
四边形是平行四边形(对角线互相平分的四边形是平行四边形)
(3)四边形不是平行四边形
因为把条件改为后,不能证明与全等.
23.如图,在四边形中,,为中点,延长到点,使.
(1)求证:;
(2)求证:四边形为平行四边形;
(3)若,,,求四边形的面积.
【解答】(1)证明:,
,
为中点,
,
在和中,,
,
;
(2)证明:由(1)得:,,
四边形是平行四边形,
,,
,
,,
四边形为平行四边形;
(3)解:四边形为平行四边形,
,,,
,,
,
,
,
,
,
,
四边形的面积.
24.如图,在四边形中,是上一点,交于点,,,.
(1)求证:;
(2)若,求;
(3)若,求证:四边形是平行四边形.
【解答】(1)证明:,
,
在和中,,
;
(2)解:,
,
,
,
;
(3)证明:,
,
,
,
,
,
,
,
,
,
,
,
,
,
四边形是平行四边形.
25.如图在四边形中,,,.是的中点是边上的一动点与,不重合),连接并延长交的延长线于.
(1)试说明不管点在何位置,四边形始终是平行四边形.
(2)当点在点.之间运动到什么位置时,四边形是平行四边形?并说明理由.
【解答】解:(1)
是的中点,
,
,,
.
,
,
四边形是平行四边形,
不管点在何位置,四边形始终是平行四边形;
(2)当四边形是平行四边形时,,
,
,
.
当时,四边形是平行四边形.
